Infomation and Entropy (3) Compression

Posted on Edited on In , ,

Abstract. 为了支持更有效的传输、存储和处理，我们需要对数据进行压缩（即，不简单地逐位翻译每个符号，而是用一串字符代表一段连续的符号）。

这一章前面讲的内容比较宝宝巴士，后面的宝宝巴士可拓展性比较强。整体难度中等。

经过压缩之后我们传递信息的模型可以改写为

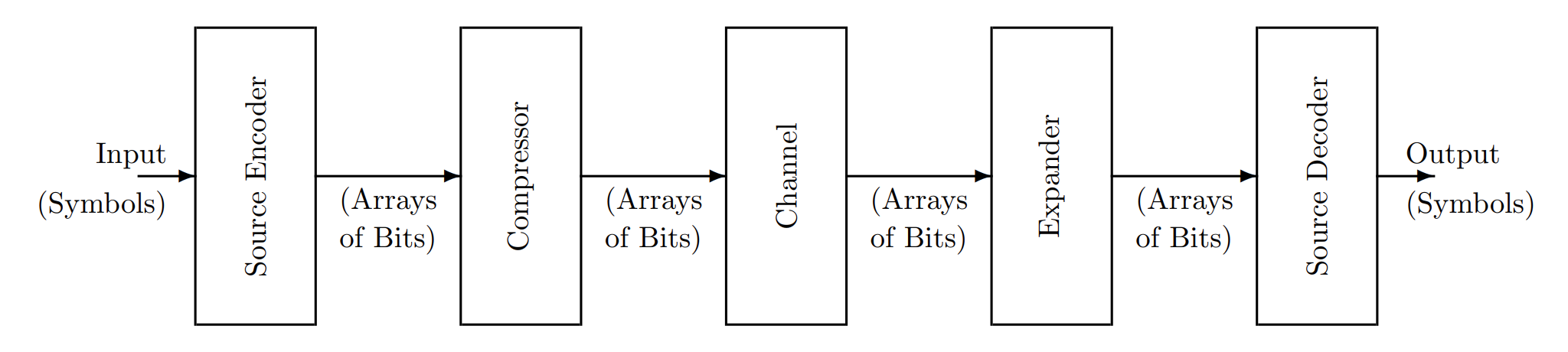
注意其中增加了两个模块 Compressor 和 Expander 来支持上面的压缩和解压缩操作。这里压缩可以分为两类。

  • Lossless / reversible. 只有在原来的编码不够高效时可以实现。
  • Lossy / irreversible. 编码已经足够高效，经过压缩之后信息有所丢失，但是 expander 可以还原出一个可以接受的近似版本。

接下来我们给出五种 reversible 压缩方式和一种 irreversible 压缩方式，每一种都各有优劣。

Variable-Length Encoding

变长编码。

前一章提到的 Morse Code，和我们熟悉的 Haffman 编码，都属于这种技巧。在这两种压缩方式当中高频出现的字有短编码，因此编码的总期望长度小于定长编码的长度。

Run Length Encoding

游程编码。

在需要编码的文本中存在大规模的连续段时可以采用这种编码（比方说你要编码一个德国国旗），压缩连续段为符号 + 重复次数的形式。

但是在文本中没有大规模连续段时这种做法是非常低效的。

Static Dictionary

对高频词单独给定编码，比如说如果 ASCII 码里面你不需要 DEL 这个东西，就可以用 127 位来编码单词 the，这样可以知道编码长度会缩小。

当然实际上我们肯定不会只用一位，而是给定一个编码和词之间的静态的对应关系，称为 Static Dictionary。

举了一个上上上个世纪的例子，即英国的 Shutter Telegraph [1]。可见其宝宝巴士。

Semi-adaptive Dictionary

可以想到对于不同的信息采用最优的字典的话长度可能会更好。那么你可以每条信息都先发字典然后再发内容本身。

但是这样做其实很傻逼，因为首先你需要把字典发过去这件事开销就非常大，其次为了找一个好的字典你需要先知道要编码的全部文本，这意味着你的算法必须是离线的（带有很大的 latency），所以这个编码也不怎么用。

Dynamic Dictionary, LZW Compression

事实上现在常用的技术是一边处理文本一边算字典。有一种算法称为 LZW Compression。

这个算法的过程如下：

Encoder

  • 初始时字典中有 ASCII 码表，以及 256: Start 和 257: End，置 tot = 258
  • 发送 $\mathtt{256}$
  • 接下来定义一个量 new_entry，初始时这个量为空。
  • 迭代整个文本，假设当前字符为 $\mathtt{c}$。
    • 令 new_entry' 为 new_entry + c。
    • 如果 new_entry' 不在字典中
      • 那么向字典中增加 tot: new_entry，tot += 1。
      • 发送 new_entry 对应的编码。
      • 令 new_entry = c
    • 否则继续迭代
  • 发送剩下的边角料和 $\mathtt{257}$

Decoder

其实写到这里很明显了，你只需要按照上面的方式动态地同步维护字典即可。这个编码是 Reversible 的。

这样你发现基本上所有长度为 $2$ 的 pattern 都会在可以接受的轮次之后被假如字典，所以说我们可以期望文本的编码长度缩小到了原始编码长度的 $\frac 12$。

Discrete Cosine Transformation

DCT 用于将图片压缩，保留和人类知觉最相关的信息，而其他稍微无关的信息则被忽略。

Discrete Linear Transformation

对于矩阵 $\mathbf{I}$，可以定义

$$
\mathcal{T}_{\mathbf{CD}}(\mathbf{I}) = \mathbf{CID}
$$

容易验证这个变换的线性性。

Discrete Cosine Transformation

考虑一张像素 $n\times n$ 的图片，假设其矩阵表示为 $\mathbf{A}$

定义矩阵 $\mathbf{C}_{n\times n}$

$$
C_{ij} = k_j\cos\left(\frac{(2i+1)j\pi}{2n}\right)
$$

其中

$$
k_j = \begin{cases}
\sqrt{\frac 1n} &, j = 1 \\
\sqrt{\frac 2n} &, \text{otherwise.}
\end{cases}
$$

可以验证 $\mathbf{C}$ 是一个正交矩阵。

定义.(Discrete Cosine Transformation)

$$
\mathcal{T}(\mathbf{A}) = \mathbf{C}^{T}\mathbf{AC}
$$

那么逆变换的形式也显然

$$
\mathcal{T}^{-1}(\mathbf{A}) = \mathbf{C}\mathbf{AC}^{T}
$$

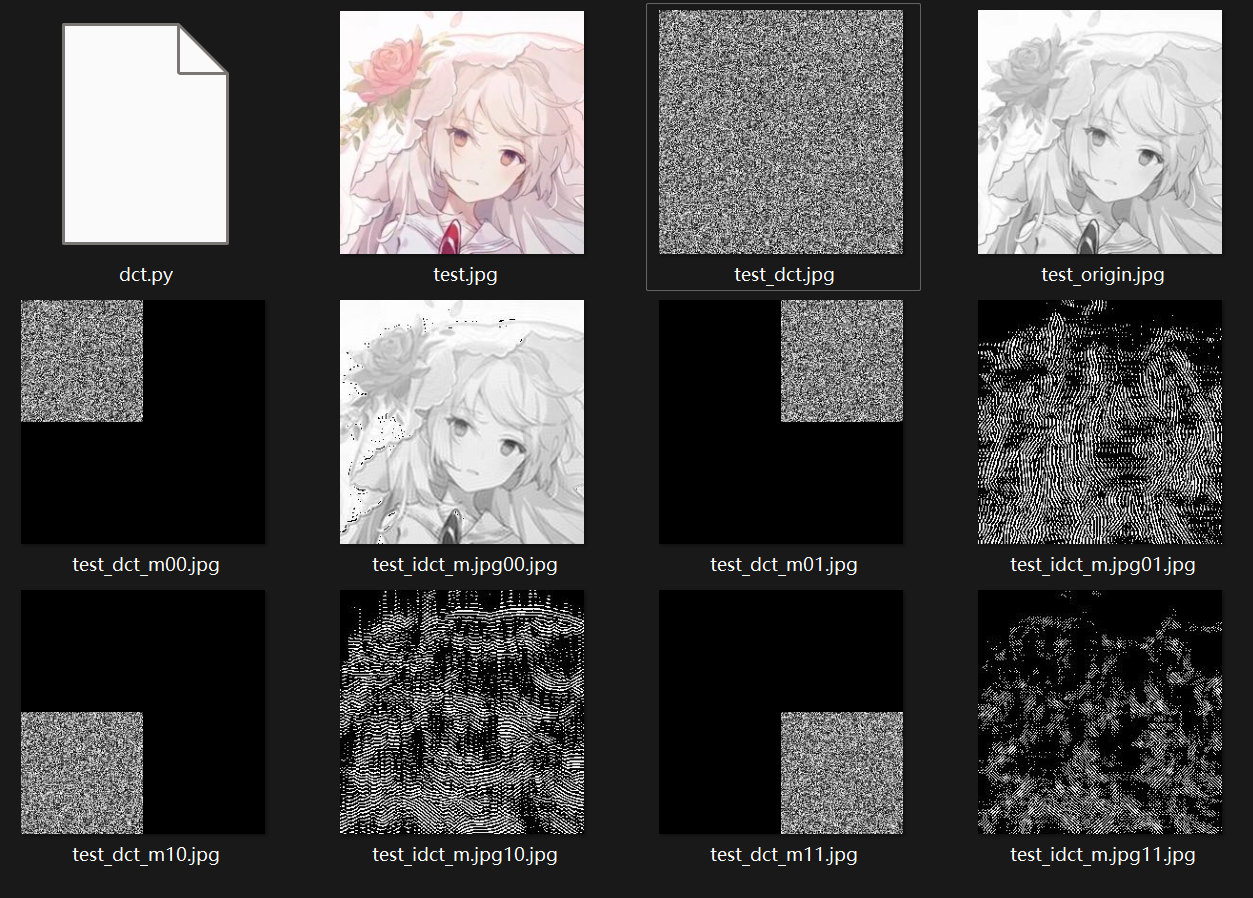
注意到这个算法实际上和离散傅里叶变换很像，只是它没有虚部。因此你可以想象这个算法还是实现了某种时域到频域的变换，高频信号全部集中在左上角。因此你只保留 DCT 结果的左上角，将其他位置全部置为 0，对图像的影响不会很大，只会有一点包浆，这样的特性使得这个算法可以用来压缩图片。而可以想象你如果保留右上、左下、右下则会得到一些抽象画。我们甚至可以语言保留右上，左下会得到一些有倾向性的条纹，而右下角则是纯抽象画。

作为测试我们写了一些 python 代码（顺便学了一些 python 语法），然后用我的头像做了一些操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
from PIL import Image
import numpy as np
from math import sqrt, cos

def save(mat, path, scalar = 1):
    tmp = np.array(mat) * scalar
    im = Image.fromarray(np.uint8(tmp))
    im.save(path)


def mult(a, b):
    res  = [ [0.0] * 256 for i in range(0, 256) ]
    for k in range(0, 256):
        for i in range(0, 256):
            for j in range(0, 256):
                res[i][j] += a[i][k] * b[k][j]
    return res


def dct(mat, type):
    c  = [ [0.0] * 256 for i in range(0, 256) ]
    ct = [ [0.0] * 256 for i in range(0, 256) ]
    k = [0.0] * 256
    n = 256
    pi = 3.141592653589793238
    k[0] = sqrt(1 / n)
    for i in range(1, 256): k[i] = sqrt(2 / n)
    for i in range(0, 256):
        for j in range(0, 256):
            c[i][j] = k[j] * cos((2 * i + 1) * j * pi / (2 * n))
            ct[j][i] = c[i][j]
    if type == 1:
        return mult(ct, mult(mat, c))
    elif type == -1:
        return mult(c, mult(mat, ct))
    else: return mult(c, ct)


def modify(mat, x = 0, y = 0):
    res = [ [0.0] * 256 for i in range(0, 256) ]
    for i in range(0, 256):
        for j in range(0, 256):
            if (i >= 128) == x and (j >= 128) == y:
                res[i][j] = mat[i][j]
    return res


def main():
    im = Image.open('E:\\Notes\\Others\\Discrete Cosine Transform\\test.jpg')
    lim = im.convert('L').resize((256, 256))
    mat = [ [0.0] * 256 for i in range(0, 256) ]
    for i in range(0, 256):
        for j in range(0, 256):
            mat[j][i] = lim.getpixel((i, j))
    save(mat, 'test_origin.jpg');
    dmat = dct(mat, 1)
    save(dmat, 'test_dct.jpg', 256)
    idmat = dct(dmat, -1)
    save(idmat, 'test_idct.jpg')
    for i in range(0, 2):
        for j in range(0, 2):
            mmat = modify(dmat, i, j)
            save(mmat, 'test_dct_m' + str(i) + str(j) + '.jpg', 256)
            immat = dct(mmat, -1)
            save(immat, 'test_idct_m.jpg' + str(i) + str(j) + '.jpg')


if __name__ == "__main__":
    main()

得到的结果如下

  1. 1.https://newmarkethistory.org.uk/newmarket-at-war/shutter-telegraph/ ↩