Revision | 信息科学中的物理学（上）力学

Abstract. 信息科学中的物理学（上）的复习笔记，内容是一些力学。

因为在另一篇笔记里面突然讲了一些力学所以把这一篇也放上来。

• 运动学
  • 曲线运动
• 质点系
  • 质心 质心运动定理
  • 碰撞
  • 火箭飞行
• 角动量定理 角动量守恒
  • 角动量守恒
  • 推导电子绕 H 核运动半径
  • 转动参考系中的惯性力
  • 开普勒第一定律的证明
    • 可用的材料
    • 径向加速度的推导
    • 求解微分方程
• 能量守恒
  • 保守力
• 定轴转动
  • 转动惯量
• 刚体的平面平行运动
  • 分解方法
  • 关键结论
  • 各守恒量的表示
• 流体力学入门

运动学

曲线运动

可以利用瞬时圆周运动的结论求解一个运动轨迹的曲率半径。求解方法由如下方程给出。

$$
\begin{cases}
a_t = \dfrac{dv}{dt} \\
a_n^2 + a_t^2 = a^2 \\
a_n = \dfrac{v^2}{\rho}
\end{cases}
$$

质点系

质心 质心运动定理

定义(质心). 称如下量为一个质点系的质心坐标

$$
\vec r_C = \frac{\sum\limits_im_i\vec r_i}{m}
$$

性质.

$$
\begin{aligned}
&\sum_i m_i\vec r_{Ci} \\
=&\sum_im_i(\vec r_i - \vec r_C) \\
=&m\vec r_C - m\vec r_C = 0
\end{aligned}
$$

根据牛顿定律可以推得如下定理

质心运动定理.

$$
\vec F = m\vec a_C
$$

其中 $\vec F$ 为合外力。你可以发现这个其实就是动量定理。

证明.

$$
\sum_i \sum_j F_{ij} = \sum_i m_i\vec a_i
$$

根据牛顿第三定律，内力相互抵消，左式等于 $\vec F$，对质心定义求二阶导，右式即为 $m\vec a_C$。

碰撞

定义(恢复系数) 两刚体发生碰撞，碰后两刚体的分离速度与碰前的接近速度成正比，即

$$
e = \frac{v_2 - v_1}{v_{20} - v_{10}}
$$

其中的 $v$ 系指两物体碰撞点的法向速度。

火箭飞行

考虑喷出气体相对火箭的速度为 $u$。假设某时刻火箭质量为 $m$，速度为 $v$。根据动量守恒可以列出如下方程

$$
mv = (m+dm)(v+dv) - dm(v+dv - u)
$$

需要注意的是 $dm$ 本身是一个负数，因为质量随时在减少，这决定了 $dm$ 前面的符号。展开并忽略二阶小量得到

$$
mdv = udm \\
$$

两边积分即可得到

$$
v_2 - v_1 = u\ln\frac{m_1}{m_2}
$$

角动量定理 角动量守恒

角动量守恒

注意和动量守恒一样，角动量可以分方向守恒。

比如说普通物理第七版的习题 2-49，实际上只需要这两个式子：

• 竖直方向角动量守恒

  $$
  mv_0l\sin \theta = mvl
  $$

• 能量守恒

  $$
  \frac 12 mv_0^2 = \frac 12 mv^2 + mgl\cos\theta
  $$

推导电子绕 H 核运动半径

这里我们接受玻尔的原子模型。

$$
\frac{ke^2}{r^2} = m\frac{v^2}{r}
$$

而角动量是量子化的

$$
mvr = n\hbar
$$

联立两个式子即可得到

$$
r = \frac{n^2\hbar^2}{kme^2}
$$

可知轨道半径正比于 $n^2$。

然后我们又有

$$
E = \frac 12 mv^2 - \frac{ke^2}{r}
$$

将 $r$ 代入这个式子可以得到 $E\propto \frac 1{n^2}$，也就是我们熟悉的巴尔末公式。

转动参考系中的惯性力

Lemma. 设矢量 $\vec A$ 在 $S$ 系中的变化率为 $\left(\dfrac{d\vec A}{dt}\right)_S$ ，在 $K$ 系中的变化率为 $\left(\dfrac{d\vec A}{dt}\right)_K$。其中 $K$ 系是一个以角速度 $\vec \omega$ 转动的转动参考系。则有

$$
\left(\dfrac{d\vec A}{dt}\right)_K + \vec \omega\times \vec A = \left(\dfrac{d\vec A}{dt}\right)_S
$$

这个式子从几何上简单理解起来是容易的，严格的证明可以用向量旋转。

所以就有

$$
v_S = v_K + \vec \omega\times \vec r
$$

然后再求一阶导

$$
a_S = a_K + 2\vec \omega\times \vec v_K + \vec \beta\times \vec r +\vec \omega\times (\omega\times \vec r)
$$

可得

$$
a_K = a_S - 2\vec \omega\times \vec v_K - \vec \beta\times \vec r -\vec \omega\times (\vec\omega\times \vec r)
$$

上面的式子中 $2\vec \omega\times \vec v_K$ 是科里奥利加速度，$\vec \omega\times (\omega\times \vec r)$ 是离心加速度，$\vec \beta\times \vec r$ 由角加速度引起。等号两边乘上 $m$ 即可得到旋转参考系中的力变换公式。$F_{Cor} = ma_{Cor}$。

开普勒第一定律的证明

可用的材料

建立极坐标系。我们有的材料只有：

牛顿第二定律

$$
\frac{GMm}{r^2}\vec{e_r} = ma\vec {e_r}
$$

角动量守恒

$$
mr^2\theta’ = L
$$

问题在于 $a$ 可能不是特别显然。所以我们有必要进行一些推导。

径向加速度的推导

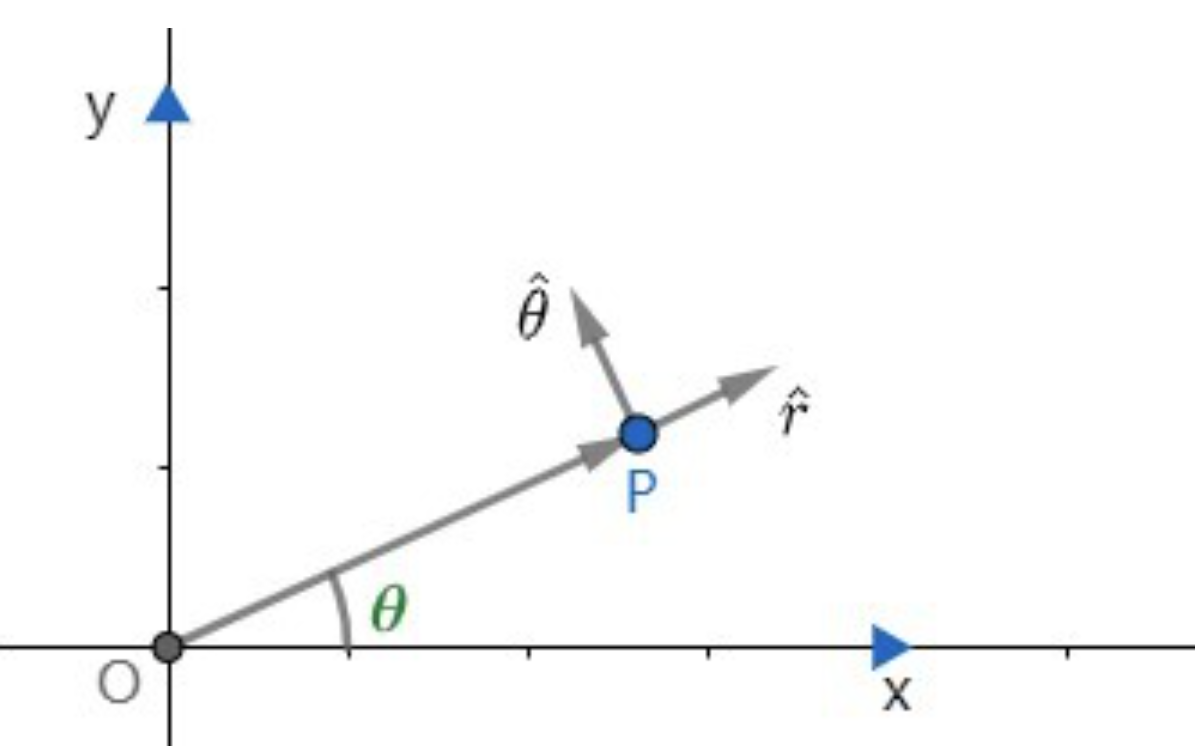
首先有 $\vec{e_r}$ 和 $\vec{e_{\theta}}$ 的导数的关系：

$$
d\vec{e_\theta} = \theta’r(-\vec{e_r})dt \\
d\vec{e_r} = \theta’\vec{e_\theta}dt
$$

之所以需要这个式子，是因为我们不希望最后式子里面有 $d\vec e$ 状物。

$$
\begin{aligned}
\vec v &= \frac{dr\vec{e_r}}{dt} \\
&=r’\vec{e_r} + rd\vec{e_r} \\
&=r’\vec{e_r} + r\theta’\vec{e_\theta}
\end{aligned}
$$

继续求导，这里跳过过程直接得到结论

$$
\vec a = (r’’ - r\theta’^2)\vec{e_r} + (2r’\theta’ + r\theta’’)\vec{e_\theta}
$$

求解微分方程

现在我们得到了 $(1)$ 式中的 $a = r’’ - r\theta’^2$。代入之后可以得到下面的二阶微分方程

$$
\frac{GM}{r^2} = r\theta’^2 - r’’
$$

这玩意的求解技术含量很高，所幸我们提前预知了 $F(r, \theta) = 0$ 是圆锥曲线的参数方程，因此 $\frac{1}{r}$ 的形式应当简单，而且等号左边的 $r$ 全在分母上面，也许想要解这个方程必须从 $\frac 1r$ 的角度进行考虑。

令 $A = \frac 1r$。

$$
dA = -\frac{1}{r^2}dr
$$

现在考虑求 $r’’$

$$
\begin{aligned}
r’ &= \frac{dr}{dt} = \frac{dr}{d\theta}\theta’= -\frac{r^2dA}{d\theta}\cdot\frac{L}{mr^2} \\
&= -\frac{LdA}{md\theta}\\
r’’&=\frac{dr’}{dt} = \frac{d\left(-\frac{LdA}{md\theta}\right)}{d\theta}\theta’\\
&=-\frac{L^2d^2A}{m^2r^2d\theta^2}
\end{aligned}
$$

将这个结果代入原微分方程

$$
\frac{GM}{r^2} = \frac{L^2}{m^2r^3} + \frac{L^2d^2A}{m^2r^2d\theta^2} \\
\frac{d^2A}{d\theta^2} = -A + \frac{GMm^2}{L^2}
$$

令 $y = A - \frac{GMm^2}{L^2}$，则 $y=-y’’$， $y = C\cos(\theta + \varphi)$。那么

$$
A = C\cos(\theta + \varphi) + \frac{GMm^2}{L^2}\\
r = \frac{\frac{L_2}{GMm^2}}{1 + C_1\cos(\theta + \varphi)}
$$

其具有圆锥曲线性。

能量守恒

保守力

定义. 称满足如下条件的力为保守力

$$
\oint Fds = 0
$$

下面给出引力是保守力的证明。考虑下图

那么万有引力对这一段小位移做的功为
$$
dA = \vec F\cdot d\vec r = F |d\vec r|\cos\theta \\
$$
从上图中可以看出几何关系 $|d\vec r|\cos \theta = dr$，于是 $dA = Fdr$，积分可知其确实满足保守力的条件。

定轴转动

转动惯量

背诵一些比较常见的。

• 薄圆环对中轴 $J=mr^2$
• 薄圆环对直径 $J = \frac 12 mr^2$
• 圆盘对中轴 $J=\frac 12 mr^2$
• 圆筒对中轴 $J = \frac 12m(r_1^2 + r_2^2)$
• 圆柱对中轴 $J = \frac 12 mr^2$
• 圆柱对垂直平分轴 $J = \frac 14mr^2 + \frac 1{12}ml^2$
• 细棒对垂直平分线 $J = \frac 1{12}ml^2$
• 细棒对端点 $\frac 13ml^2$
• 球沿直径 $\frac 25mr^2$
• 球壳沿直径 $\frac 23 mr^2$

刚体的平面平行运动

分解方法

常用两种：

• 质心法，下一节中均考虑这种分解
• 瞬心法

关键结论

质心运动定理（动量定理）

$$
\vec F = m \frac{d\vec v_c}{dt} \\
\vec F dt = d\vec p
$$

相对质心转动定理（角动量定理）

$$
M = J_c\frac{d\omega}{dt}=J_c\beta \\
Mdt = dL_c
$$

Hint. 这是因为以质心为参考系，惯性力不会贡献力矩。

动能定理

$$
W = \Delta E_k
$$

各守恒量的表示

考虑如下做平面平行运动的刚体。

相对平面内任意一点的动量，角动量和动能的式子可能并不平凡。

动量

$$
p = m\vec v_C
$$

角动量

$$
\vec L_O = mv_Cl_{OC}\sin \theta+J_c\omega
$$

证明.

该刚体的角动量为各质量元的总角动量。

$$
\begin{aligned}
\vec L_O &= \sum_i m_i\vec r_{Oi}\times \vec v_i \\
&= \sum_i m_i(\vec r_{OC} + \vec r_{Ci})\times (\vec v_C + \vec r_{Ci}\times \vec \omega) \\
&=\sum_im_i\vec r_{OC} \times \vec v_C + \sum_im_i\vec r_{OC}\times(\vec r_{Ci}\times \vec \omega) \\&+ \sum_i m_i\vec r_{Ci}\times \vec v_C + \sum_i m_ir_{Ci}\times (\vec r_{Ci}\times \vec \omega) \\
&=\vec r_{OC} \times \vec v_C\sum_im_i + \vec r_{OC}\times\left(\sum_im_i\vec r_{Ci}\times \vec \omega\right) \\&+ \left(\sum_i m_i\vec r_{Ci}\right)\times \vec v_C + \sum_i m_ir_{Ci}\times (\vec r_{Ci}\times \vec \omega) \\
\end{aligned}
$$

注意根据质心定义有

$$
\sum_i m_i\vec r_{Ci}=0
$$

所以该式二三项都为 0，而一四项和为

$$
v_Cl_{OC}\sin \theta + J\omega
$$

动能

$$
E_k = \frac 12 mv^2 + \frac 12 J\omega^2
$$

推导是同一个道理。

Hint. 注意质心的定义。

例题

只做 $(1), (2)$，因为 $(3), (4)$ 其实很简单，只需要分解为质心的平动（抛体运动）和转动即可。

1. 以转轴为轴，这是一个定轴转动。

   有动量守恒

   $$
   mv_0 = (m + M)v_C
   $$

   角动量守恒

   $$
   mx^2\frac{v_0}{x} = \frac 13 Ml^2\frac{2v_C}{l}+mx^2\frac{v_C}{x}
   $$

   $(28)x - 29$ 即可得出 $x = \frac 23 l$。

2. 首先可以写出新质心的位置 $x_0$，新质量 $M’$，碰撞后的速度 $\omega_0$

   将作用力分解到沿杆和垂直杆方向，分别记为 $N_1, N_2$。

   分方向使用质心运动定理

   $$
   M’a_t = N_2 - mg\sin \theta \\
   M’a_n = N_1 - mg\cos \theta
   $$

   有线量和角量的关系

   $$
   a_t = \omega^2x_0\\
   a_n = x_0\beta
   $$

   能量守恒

   $$
   J\omega^2 - J\omega_0^2 = M’gx_0(1-\cos\theta)
   $$

   角动量定理

   $$
   J\beta = mg\sin\theta
   $$

   联立上述六个方程即得答案。

Hint. 在上述过程中我们的操作体现了下述几个重要思想：

1. 将所求解量适当分解。
2. 将刚体视为质点系，考虑质心运动定理。

流体力学入门

伯努利方程

重力场中存在一定常流场，则同一流管内部
$$
p + \frac 12 \rho v^2 + \rho g h = C
$$
推导.

考虑一段流管从 $ab$ 流到 $ab’$，这时差分之后的两端趋近于 0，可以将其中速度，压强，截面积等均看作不变。

$$
\Delta E = \Delta m(\frac 12 v_1^2 + gh_1 - \frac 12 v_2^2 - gh_2)
$$

系统所受外力只有压力

$$
A = f_1v_1\Delta t - f_2v_2\Delta t = p_1S_1v_1\Delta t - p_2S_2v_2\Delta t
$$

此外还有两个式子，给定截面流量相等，以及质量和截面及流速的关系。

$$
S_1v_1 = S_2v_2 \\
\Delta m = \rho Sv\Delta t
$$

由于 $A = \Delta E$，代入即可得到该方程。