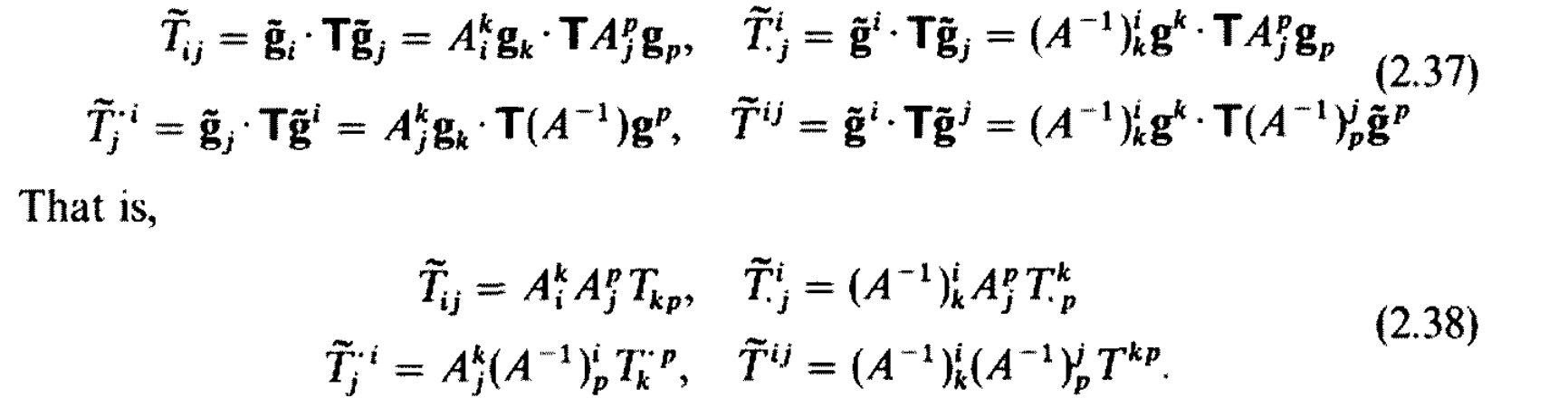Tensor Analysis (2) General Bases and Tensor Notation

Posted on Edited on In , ,

Abstract. 我们常常需要分量式（Component）以便于计算。为了兼容任意的坐标系，我们需要引入 General Bases，并推导向量和张量的坐标表示和坐标变换。

General Bases

考虑取 $\mathbb{R}^3$ 中的一组基 $\mathbf{g}_1, \mathbf{g}_2, \mathbf{g_3}$，则任意一个向量可以被唯一表出。

$$
\mathbf{v} = \sum_{i=1}^3 v^i\mathbf{g_i}
$$

注意这里的 $i$ 在上标和下标位置上都表示编号而不是乘方，这个记号是一个伏笔。

The Jacobian of a Basis Is Nonzero

Definition 2.1.(Jacobian Matrix) $G = (\mathbf{g}_1^T, \mathbf{g}_2^T, \mathbf{g_3}^T)$。

Definition 2.2.(Jacobian) $J = \mathrm{det~}G$。

根据线性代数我们知道如果 $\mathbf{g}_1, \mathbf{g}_2, \mathbf{g}_3$ 线性无关，必有 $J\ne 0$。

The Summation Convention

由于我们的讨论都是 $\mathbb{R}^3$ 下的，所以求和指标是确定的。而且求和中的 $i$ 是一个 dummy variable。简便起见并且不丢失任何信息地，我们可以约定：去掉求和符号，用下面的方法来表示分解式

$$
\mathbf{v} = v_i\mathbf{g}^i
$$

这个记号表示分解式当且仅当两个相同的 dummy index 一个是上标，一个是下标。举例来说 $v^iv_i = \sum_i v^iv_i$，而 $v^iv^i$ 可能是 $v^1v^1, v^2v^2$ 或者 $v^3v^3$。

这个约定是爱因斯坦提出的，称为爱因斯坦求和约定。这个约定现在看起来非常奇怪，但是到第六节之后它的简便性就会有所体现。

Computing the Dot Product in a General Basis

很明显在任意基下面我们就不能用原来对位相乘的方法来计算点积。正确的表达式是

$$
\mathbf{u}\cdot\mathbf{v} = u^iv^j\mathbf{g}_i\cdot\mathbf{g}_j
$$

这个是一个九项的式子，为了让它更简单我们引入 reciprocal base vectors。

Reciprocal Base Vectors

先考虑二维的情形，现在要计算 $\mathbf{u}\cdot\mathbf{v}$，我们将 $u$ 分解为 $\mathbf{u} = u^1\mathbf{g}_1 + u^2\mathbf{g}_2$。

现在我们找一组新的基 $\mathbf{g}^1, \mathbf{g}^2$，将 $\mathbf{v}$ 用这两个向量表出，然后写出乘积式。

$$
\begin{aligned}
\mathbf{u}\cdot\mathbf{v} &= (u^1\mathbf{g}_1 + u^2\mathbf{g}_2)(v_1\mathbf{g}^2 + v_2\mathbf{g^2}) \\
&= u^1v_1\mathbf{g}_1\mathbf{g}^1+u^1v_2\mathbf{g}_1\mathbf{g}^2+u^2v_1\mathbf{g}_2\mathbf{g}^1+u^2v_2\mathbf{g}_2\mathbf{g}^2
\end{aligned}
$$

我们希望这个式子保持原来对点相乘的简单形式，也就是要求

$$
g_ig^i = 1, g^ig^j = 0 (i\ne j)
$$

事实上这时候，从几何上已经非常容易理解了，如下图所示我们可以找到 reciprocal base vector

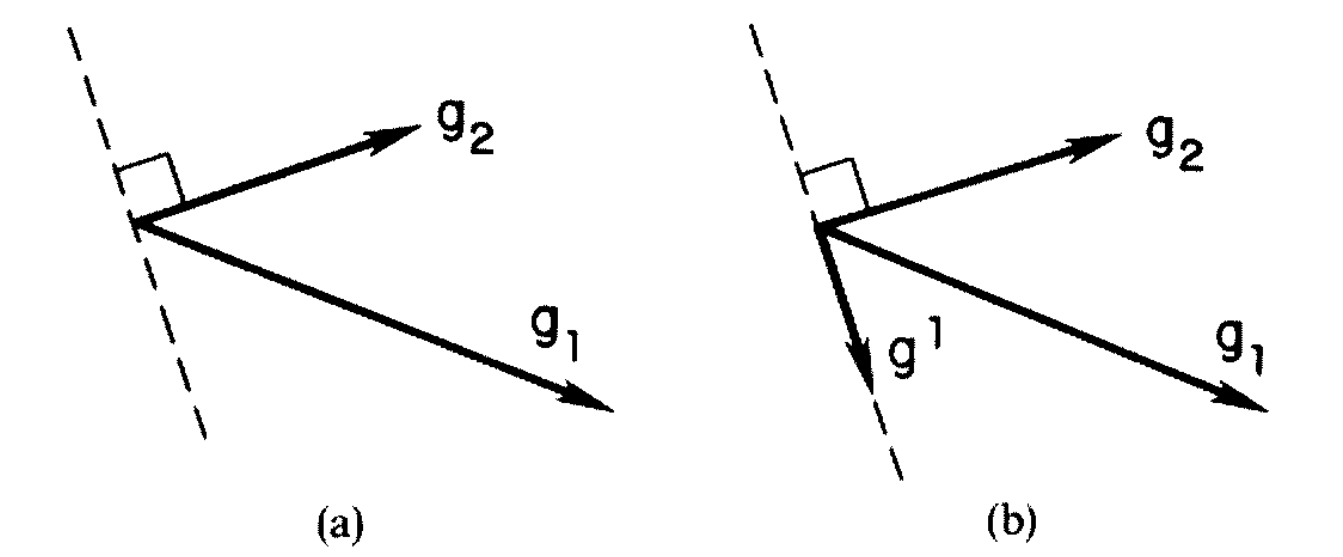
但是我们还希望有一个代数上的方法。

首先写出 $\mathbf{g}_1, \mathbf{g}_2, \mathbf{g}_3$ 的 Jacobian Matrix $G_1$ 和 $\mathbf{g}^1, \mathbf{g}^2, \mathbf{g}^3$ 的 Jacobian Matrix $G_2$。

拓展并翻译上面的条件，就是

$$
\mathbf{g}_i (\mathbf{g}^i)^T = \delta_i^j
$$

其中 $\delta_{ij}$ 是 Kronecker delta 函数，满足

$$
\delta_i^j = [i = j]
$$

换言之

$$
G_1G_2^T = I
$$

也就是

$$
G_2 = (G_1^{-1})^T
$$

The Roof (Contravariant) and Cellar (Covariant) Components of a Vector

翻译是逆变分量 （Contravariant Component）和协变分量（Covariant Component）。这个名字的意义暂时不是很明确，方便起见我们下文均采用 Roof Component 和 Cellar Component 的说法。

也就是上面的在 $\mathbf{g}_i$ 和 $\mathbf{g}^i$ 下的分解。你可以这样记忆，Roof 是指 $v^i\mathbf{g_i}$ 中 $v^i$ 是上标（Roof）。而且由于某些巧合，这里的 Roof 和 Cellar 和矩阵的 Row 和 Column 是联系的。

推导 Cellar Components 可以采用如下方法。

$$
(v_i\mathbf{g}^i)\cdot \mathbf{g}_j = v\cdot\mathbf{g}_j
$$

将左式展开

$$
\begin{aligned}
\mathrm{LHS} &= v_i\mathbf{g}^i\cdot\mathbf{g}_j \\
&= v_i\delta_j^i \\
&= v_j
\end{aligned}
$$

因此

$$
v_i = \mathbf{v}\cdot\mathbf{g}_i \tag{1}
$$

可以用同样的方法推出

$$
v^j = \mathbf{v}\cdot\mathbf{g}^j \tag{2}
$$

这个推导方法和我们熟知的反演非常相似。

这也启发我们 kronecker delta 函数可以视为一种 replacement operator（换位算符）。形式化地

$$
v^i\delta_i^j = v^j
$$

Simplification of the Component Form of the Dot Product in a General Basis

根据上文的铺垫我们容易进行以下推导

$$
\begin{aligned}
\mathbf{u}\cdot\mathbf{v} &= u^iv_j\mathbf{g}_i\cdot\mathbf{g}^j \\
&= u^iv_j\delta_i^j \\
&= u^iv_i
\end{aligned}
$$

当然你一开始如果将 $\mathbf{u}$ 分解为 Cellar Components，那么也可以写成

$$
\mathbf{u}\cdot\mathbf{v} = u_iv^i
$$

Computing the Cross Product in a General Basis

现考虑如何求解 $\mathbf{u}\times\mathbf{v}$ 在 General Basis 下面的分解式，不妨求解它的 Cellar Components。

$$
\mathbf{u}\times\mathbf{v} = (\mathbf{u}\times\mathbf{v})_k\mathbf{g}^k
$$

对于 $(\mathbf{u}\times\mathbf{v})_k$，将 $\mathbf{u}, \mathbf{v}$ 分解为 Roof Components，然后利用上一节的结论

$$
\begin{aligned}
(\mathbf{u}\times\mathbf{v})_k &= ((u^i\mathbf{g}_i)\times(v^j\mathbf{g}_j))\cdot \mathbf{g}_k \\
&= u^iv^j(\mathbf{g}_i\times\mathbf{g}_j)\cdot\mathbf{g}_k
\end{aligned}
$$

后面的混合积我们是熟悉的，如果 $i, j, k$ 两两不同，那么得到的东西是 $\pm J$（J 是 $\mathbf{g}_1, \mathbf{g}_2, \mathbf{g}_3$ Jacobian），否则为 $0$。这里我们引入 Levi-Civita 记号，其中

$$
\epsilon_{ijk} = \begin{cases}
J, & i, j, k \text{ is an even permutation of } (1, 2, 3) \\
-J, & i, j, k \text{ is an odd permutation of } (1, 2, 3) \\
0, & \text{otherwise}
\end{cases}
$$

然后叉乘可以改写成

$$
\mathbf{u}\times\mathbf{v} = \epsilon_{ijk}u^iv^j\mathbf{g}^k
$$

接下来，如果需要 $\mathbf{u}\times\mathbf{v}$ 的 Roof Component，这个推导和上面的过程是高度相似的，只是现在混合积变成了 $\mathbf{g}^1, \mathbf{g}^2, \mathbf{g^3}$ 的 Jacobian，根据 Reciprocal Base Vectors 的关系，可以知道此时的 Jacobian 是 $J^{-1}$，因此 Levi-Civita 记号需要相应改写为

$$
\epsilon^{ijk} = \begin{cases}
J^{-1}, & i, j, k \text{ is an even permutation of } (1, 2, 3) \\
-J^{-1}, & i, j, k \text{ is an odd permutation of } (1, 2, 3) \\
0, & \text{otherwise}
\end{cases}
$$

叉乘可以写作

$$
\mathbf{u}\times\mathbf{v} = \epsilon^{ijk}u_iv_j\mathbf{g}_k
$$

显而易见

$$
\epsilon_{ijk} = J^2\epsilon^{ijk}
$$

Hint. $\epsilon_{ijk}$ 和 $\epsilon^{ijk}$ 又称为 Permutation Tensor 的 Cellar Component 和 Roof Component（【Fixme：Exercise 2.13】）

Proposition 1.

$$
\epsilon^{ijk}\epsilon_{pqr} = \left\vert\begin{matrix}
\delta^i_p & \delta^i_q & \delta^i_r \\
\delta^j_p & \delta^j_q & \delta^j_r \\
\delta^k_p & \delta^k_q & \delta^k_r
\end{matrix}\right\vert
$$

Proof. 只需要验证 $ijk$ 和 $pqr$ 均取 123 的情形，其余情况或者平凡或者可以对称得到。$\square$

Corollary 1.

$$
\epsilon^{ijk}\epsilon_{pqk} = \delta_p^i\delta_q^j - \delta_q^i\delta_p^j
$$

A Second Order Tensor Has Four Sets of Components in General

接下来我们考虑二阶张量在 General Bases 下的分量。

首先我们可以将作用的向量分解为 Roof Component，此时我们需要知道

$$
\mathbf{T}g_j = \mathbf{T}_j
$$

然后对得到的东西分解为 Cellar Component，此时我们需要知道

$$
T_{ij}\mathbf{g}^i = \mathbf{T}_j
$$

套用式 $(6.1)$，得到

$$
T_{ij} = \mathbf{g}_i\cdot\mathbf{Tg}_j
$$

然后我们试图将上面的式子写成此前定义的直积的形式。

$$
\begin{aligned}
\mathbf{Tv} &= \mathbf{T}(v^j\mathbf{g}_j) \\
&= v^j\mathbf{T}\mathbf{g}_j \\
&= v^j\mathbf{T}_j \\
&= v^jT_{ij}\mathbf{g}^i \\
&= T_{ij}(\mathbf{g}^j\cdot v)\mathbf{g}^i \\
&= T_{ij}\mathbf{g}^i\mathbf{g}^j(\mathbf{v})
\end{aligned}
$$

换言之

$$
\mathbf{T} = T_{ij}\mathbf{g}^i\mathbf{g}^j
$$

这称为 $\mathbf{T}$ 的 Cellar Component。

类似于我们之前的提取思路，我们将基全部换成对应的 reciprocal base vector，可以得到

$$
T^{ij} = \mathbf{g}^i\cdot\mathbf{Tg}^j, \qquad \mathbf{T} = T^{ij}\mathbf{g}_i\mathbf{g}_j
$$

这称为 $\mathbf{T}$ 的 Roof Component。

可以想象还有两个 Mixed Component。

$$
T^i_{\cdot j} = g^i\cdot\mathbf{Tg}_j, T^{\cdot i}_j = \mathbf{g}_j\mathbf{Tg}^i
$$

一般地 $T^i_{\cdot j}\ne T^{\cdot i}_j$。同理可以证明

$$
\mathbf{T} = T^i_{\cdot j}\mathbf{g}_i\mathbf{g}^j = T^{\cdot i}_j\mathbf{g}^j\mathbf{g}_i
$$

如果 $\mathbf{T}$ 是对称的，那么有

$$
\begin{aligned}
T_{ij} &= \mathbf{g}_i\cdot\mathbf{Tg} &\\
&= \mathbf{g}_j\cdot\mathbf{T}^T\mathbf{g}_i & (\text{Definition of } \mathbf{T}^T) \\
&= \mathbf{g}_j\cdot\mathbf{T}\mathbf{g}_i & (\mathbf{T}\text{ is Symmetric}) \\
&=T_{ji}
\end{aligned}
$$

这表明矩阵 $(T_{ij})$ 也是对称的，类似地 $(T^{ij})$ 也是对称的，但是两个 Mixed Component 的矩阵则未必是对称的。你会发现这里存在某种交叉相等的关系。

Change of Basis

在给定的参考系下，向量和张量都不依赖于坐标系的选取，换言之他们都是 geometric invariant。当我们选取的基底变化时，变化的是他们的分量式而不是其本身。

下面我们希望推导坐标变换时张量的 component 的表示。

考虑一组新的基 $\widetilde{\mathbf{g}}_i$，它和 $\mathbf{g}_i$ 的关系如下

$$
\widetilde{\mathbf{g}}_i = A_i^j\mathbf{g}_j
$$

或者用矩阵的形式表示（这里基底都写成列向量，$A_i^j$ 是 $A$ 的第 $i$ 列第 $j$ 行）

$$
\widetilde{G} = GA
$$

由于 $G, \widetilde{G}$ 都可逆（它们的列向量都是基），$A$ 也可逆，因此

$$
G = \widetilde{G}A^{-1}
$$

或者写成分量的形式

$$
\mathbf{g}_i = (A^{-1})_i^j\widetilde{\mathbf{g}}_j
$$

将两边求逆，还可以得到

$$
\begin{aligned}
&\widetilde{G}^{-1} = A^{-1}G^{-1}, & &\mathbf{\widetilde{g}}^i = (A^{-1})_j^i\mathbf{g}^j \\
&G^{-1} = A\widetilde{G}^{-1}, & &\mathbf{g}^i = A_j^i\widetilde{\mathbf{g}}^j
\end{aligned}
$$

以及坐标变换后向量的坐标表示

$$
\widetilde{v}_i = \widetilde{\mathbf{g}}_i\cdot\mathbf{v} = A_i^j\mathbf{g}_j\cdot \mathbf{v} = A_i^jv_j
$$

上面的结果经过一些琐碎的推导也可以得到张量的坐标变换公式