QEC Workshop | 1 概述
Abstract. 本文收录于 合集(量子纠错研讨班学习笔记)。本章以经典的重复码引出量子纠错码 bit flip code 和 phase flip code,然后刻画了量子线路的错误模型,最后介绍几个最广泛使用的稳定子体系和几个典型的纠错码。
引子:从经典纠错码到量子纠错码
我们从经典的有噪信道和作为应对的经典纠错码谈起。在一个信道中,一种“错误”可以被一个函数 $E: x\mapsto x_{\text{err}}$ 刻画,其中 $x$ 是欲通过信道发送的内容,$x_{\text{err}}$ 是实际上传输到信道另一端的内容。例如,“传输的第一位发生翻转”就是一种可能的错误,对应的函数是 $x_1…x_n \mapsto (\neg x_1)…x_n$。
考虑最简单的 $p$-binary symmetric channel,即通过该信道发送的每个比特有 $p$ 的概率发生翻转。在经典信道上,一个老生常谈的纠错码是$3$-重复码:
$$
\begin{aligned}
\textsf{Enc}(0) = 000 \quad {\color{lightgray} \text{denoted $0_L$ (the logical $0$)} } \\
\textsf{Enc}(1) = 111 \quad {\color{lightgray} \text{denoted $1_L$ (the logical $1$)} }
\end{aligned},\qquad\begin{aligned}
\textsf{Dec} = \text{Majority}
\end{aligned}
$$
当然,这个纠错码只能应对错误不超过 $1$ 位(或者 $\lfloor (r - 1) / 2 \rfloor$,对于 $r$-重复码)。在经典情况下,我们用以下定义来刻画一个纠错码可以纠正的错误:
定义 1.1. 我们称一个纠错码 $(\cdot)_L$ 能够纠正一个集合 $\mathcal{E}$ 中的错误,当且仅当
$$
\forall E_1, E_2\in \mathcal{E}, \forall x, y, \qquad E_1(x_L) \ne E_2(y_L)
$$
显然重复码不能直接应用到量子纠错之中,因为有我们熟知的不可克隆性定理。当然,你可以考虑如下的电路

这会将 $|\varphi\rangle := \alpha |0\rangle + \beta |1\rangle$ 映射到 $\alpha |000\rangle + \beta|111\rangle$ 而非 $|\varphi\rangle|\varphi\rangle|\varphi\rangle$,和经典情况下不完全相同。
此处我们尚且没有定义什么是“错误”,姑且将其理解为一个复线性映射(在第 2 节中将给出详细阐释)。如果错误只能具有以下形式:$\mathcal{U}_1\otimes\mathcal{U_2}\otimes\mathcal{U_3}$,其中 $\mathcal{U}_i$ 要么是 $\mathcal{I}$,要么是 Pauli $\mathcal{X}$,且 $\mathcal{X}$ 至多有一个,那么,我们还是可以通过测量这三个物理比特是否两两不同来知道发生了两类错误。具体地,引入两个辅助比特,定义 $s_1 = \varphi_{L1}\oplus \varphi_{L2}, s_2 = \varphi_{L2} \oplus \varphi_{L3}$(可以用 $\mathcal{CNOT}$ 门计算),测量得到 $s_1, s_2$ 之后,有
- 若测出 $00$,便知道错误是 $\mathcal{III}$;
- 若测出 $01$,便知道错误是 $\mathcal{IIX}$;
- 若测出 $10$,便知道错误是 $\mathcal{XII}$;
- 若测出 $11$,便知道错误是 $\mathcal{IXI}$。
因此,我们可以使用 Toffoli 门进行纠错。此处的测量结果在量子纠错中有专门的术语,称为症状(Syndrome)。完整的实现纠错的电路如下所示:
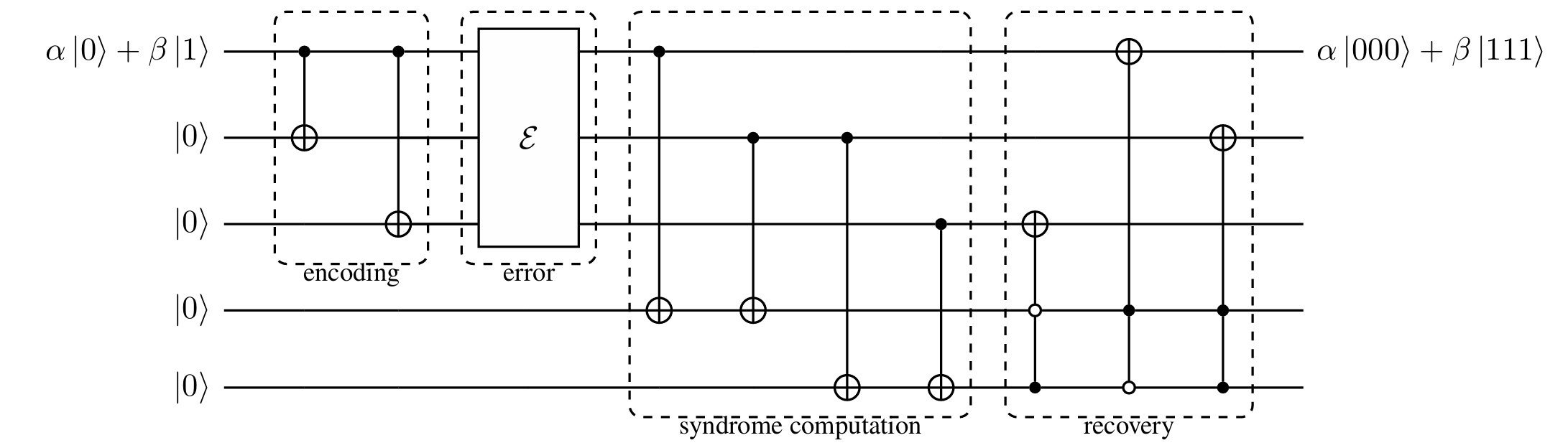
该纠错方法因为能够纠正比特翻转错误(Pauli $\mathcal{X}$)而得名 bit-flip code。当然因为它能纠正的错误过少,所以不 practical。如果将错误的形式改成 $\mathcal{U}_i$ 要么是 $\mathcal{I}$ 要么是 $\mathcal{Z}$,且 $\mathcal{Z}$ 至多有一个,则惟须做一次 phase kickback。具体来说,就是如下电路。这个电路被称为 phase-flip code。
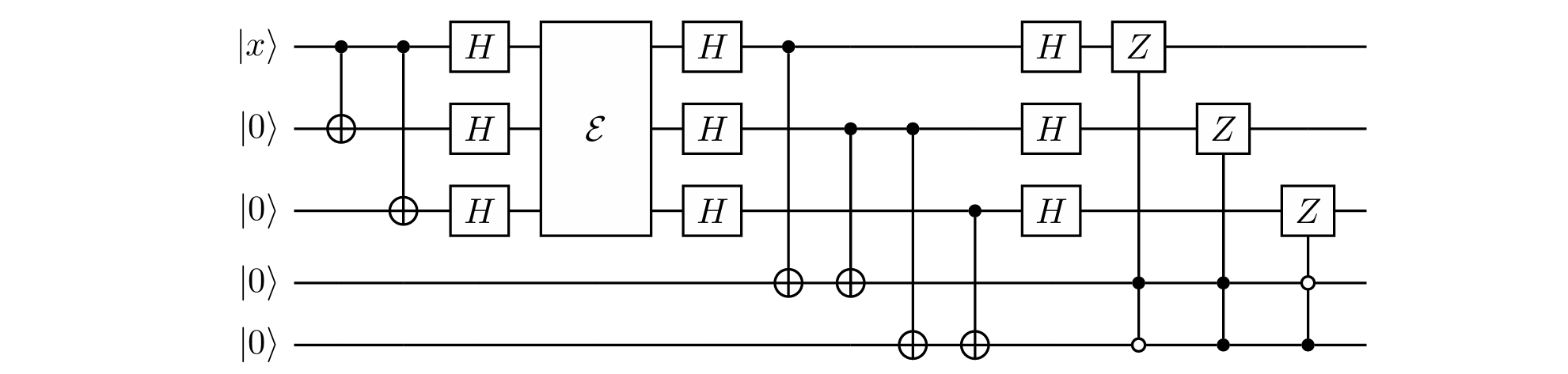
将这两种纠错码结合起来,得到所谓的 Shor Code(参见第 3 节)。在下文中我们会看到,这种纠错码能够纠正的错误相当广泛。
接下来的篇幅中,我们的主要任务是补上本节中的几个未形式化的洞(什么是量子计算过程中的错误、怎么定义一个纠错码能够纠正某错误),以及讲解几个常用的纠错码。
QEC 的错误模型
量子计算以何故产生错误?因为我们难以实现真正的孤立系统。因此演化时,某酉变换 $\mathcal{U}_{SE}$ 将作用于系统的态和环境的态之张量积 $|\varphi\rangle_S|0^n\rangle_E$,导致出现错误。不妨先考虑最简单的单量子比特的系统,此时写出 $\mathcal{U}_{SE}$ 作用的表达式:
$$
\begin{aligned}
|0\rangle_S|0^n\rangle_E \xmapsto{\mathcal{U}_{SE}} \alpha_{00}|0\rangle_S|\phi_{00}\rangle_E + \alpha_{01}|1\rangle_S|\phi_{11}\rangle_E \\
|1\rangle_S|0^n\rangle_E \xmapsto{\mathcal{U}_{SE}} \alpha_{10}|0\rangle_S|\phi_{10}\rangle_E + \alpha_{11}|1\rangle_S|\phi_{11}\rangle_E
\end{aligned}
$$
其中 $\alpha_{i0}^2 + \alpha_{i1}^2 = 1$。观察形式,忽略环境态可见,本质上,这还是该 qubit 以一定概率发生了某种“翻转”。受此启发,我们尝试将 Error 建模成 Pauli 算符之线性组合,毕竟 Pauli 算符构成二维复线性变换的一组基。不妨设 $|\psi\rangle_S := \beta |0\rangle_S + \gamma|1\rangle_S$,则有
$$
\begin{aligned}
&\mathcal{U}_{SE}|\psi\rangle_S|0^n\rangle_E \\
&= \beta(\alpha_{00}|0\rangle_S|\phi_{00}\rangle_E + \alpha_{01}|1\rangle_S|\phi_{11}\rangle_E) + \gamma(\alpha_{10}|0\rangle_S|\phi_{10}\rangle_E + \alpha_{11}|1\rangle_S|\phi_{11}\rangle_E) \\
&= (\beta|0\rangle_S + \gamma |1\rangle_S)\frac{\alpha_{00}|\phi_{00}\rangle_E + \alpha_{11}|\phi_{11}\rangle_E}{2} + (\beta|1\rangle_S + \gamma |0\rangle_S)\frac{\alpha_{01}|\phi_{01}\rangle_E + \alpha_{10}|\phi_{10}\rangle_E}{2} \\
&+ (\beta|0\rangle_S - \gamma |1\rangle_S)\frac{\alpha_{00}|\phi_{00}\rangle_E - \alpha_{11}|\phi_{11}\rangle_E}{2} + (\beta|1\rangle_S - \gamma |0\rangle_S)\frac{\alpha_{01}|\phi_{01}\rangle_E - \alpha_{10}|\phi_{10}\rangle_E}{2}\\
&= \alpha_I|\psi\rangle_S|\phi_I\rangle_E + \alpha_XX|\psi\rangle_S|\phi_X\rangle_E + \alpha_ZZ |\psi\rangle_S|\phi_Z\rangle_E + \alpha_{XZ}XZ|\psi\rangle_S|\phi_{XZ}\rangle_E
\end{aligned}
$$
当然,对于多个量子比特的系统,也不外乎是这样。至此,我们知道了量子演化过程中的任何一个错误,都是 Pauli 门的线性组合(相较于经典情况下,错误是一个 01 串到 01 串的函数)。并可以用以下定义来刻画一个纠错码能够纠正的错误:
定义 2.1. 令 $E$ 是 Pauli 算符的线性组合的一个子集。称一个纠错码 $(\cdot)_L$ 能够纠正 $E$ 中的全部错误,若对于任意的态 $|x\rangle, |y\rangle$
$$
\forall \mathcal{E}_i, \mathcal{E}_j\in E, \quad \langle x_L|\mathcal{E}_i^\dagger \mathcal{E}_j |y_L\rangle = c_{ij}\langle x_L|y_L\rangle
$$
此处 $c$ 仅取决于错误类型而不取决于逻辑比特的内容。在一些文献中也称 $\langle (\cdot)_L, E \rangle$ 构成一个量子纠错码(QECC)。
可以毫不费力的证明以下结论:
定理 2.1. 若 $(\cdot)_L$ 能纠正 $E$ 中的错误,则能纠正 $\mathrm{span}(E)$ 中的错误。
证明(Sketch). 验算。
于是,我们只需要聚焦在“纠正线性组合中的每一项对应的错误”这一工作之上。对于 $n$ 量子比特的系统,刻画“错误”的那个线性组合中的各项都是 Pauli 算符的张量积,即 Pauli 群中的元素。
定义 2.2(Pauli Group). $n$ 个 Pauli 算符的张量积,配上 $\pm 1, \pm 1$ 的系数在乘法运算下构成一个群。这个群称为 Pauli 群 $P_n$:
$$
P_n := \{ \alpha \mathcal{P}_1\mathcal{P}_2 \cdots \mathcal{P}_n : \alpha_i \in \{\pm 1, \pm i\}, P_i \in \{\mathcal{I}, \mathcal{X}, \mathcal{Y}, \mathcal{Z}\}\}
$$
Pauli 群的元素中,非平凡的 Pauli 算符个数称为该元素的权重($\mathrm{wt}$)。例如 $\mathrm{wt}(\mathcal{ZZIIX}) = 3$。这个记号用于定义后文中的码距。
注:本文中基本上不涉及 $n$ 个线性变换的复合。因此方便起见,这类 $\mathcal{P}_1…\mathcal{P}_n$ 状的记号,均表示张量积。若要表示复合,将特别用 $\circ$ 标出。
稳定子体系
量子纠错有一套常用的范式,称为 Stabilizer Formalism(稳定子体系)。我们逐步建立这一套体系。
我们先来考察 Syndrome 的本质。以 bit-flip code 为例,我们计算了 $\psi_1\oplus \psi_2$、$\psi_2\oplus \psi_3$ 的奇偶性。用一个更加量子的语言来说,我们判断了 $|\psi\rangle$ 是 $\mathcal{ZZI}$ 和 $\mathcal{IZZ}$ 的特征值为多少($1$ 还是 $-1$)的特征向量。且如果没有发生任何错误 $\mathcal{E} = \mathcal{III}$,则 $|\psi\rangle$ 是两者的特征值为 $1$ 的特征向量。具体地:
- $\mathcal{E} = \mathcal{III}$(不发生错误),特征值为 $\{+1, +1\}$;
- $\mathcal{E} = \mathcal{XII}$(第一位翻转),特征值为 $\{-1, +1\}$;
- $\mathcal{E} = \mathcal{IXI}$(第二位翻转),特征值为 $\{-1, -1\}$;
- $\mathcal{E} = \mathcal{IIX}$(第三位翻转),特征值为 $\{+1, -1\}$;
对于任意 Pauli 群中的元素,测量一个态是其特征值为多少的特征向量可以用 Phase-Kickback 配合 Controled Pauli Gate 实现。比如你现在要判断一个 $6$-qubit 态 $|\psi\rangle$ 是 $\mathcal{XXXXXX}$ 的特征值为多少的特征向量,可以使用以下电路:
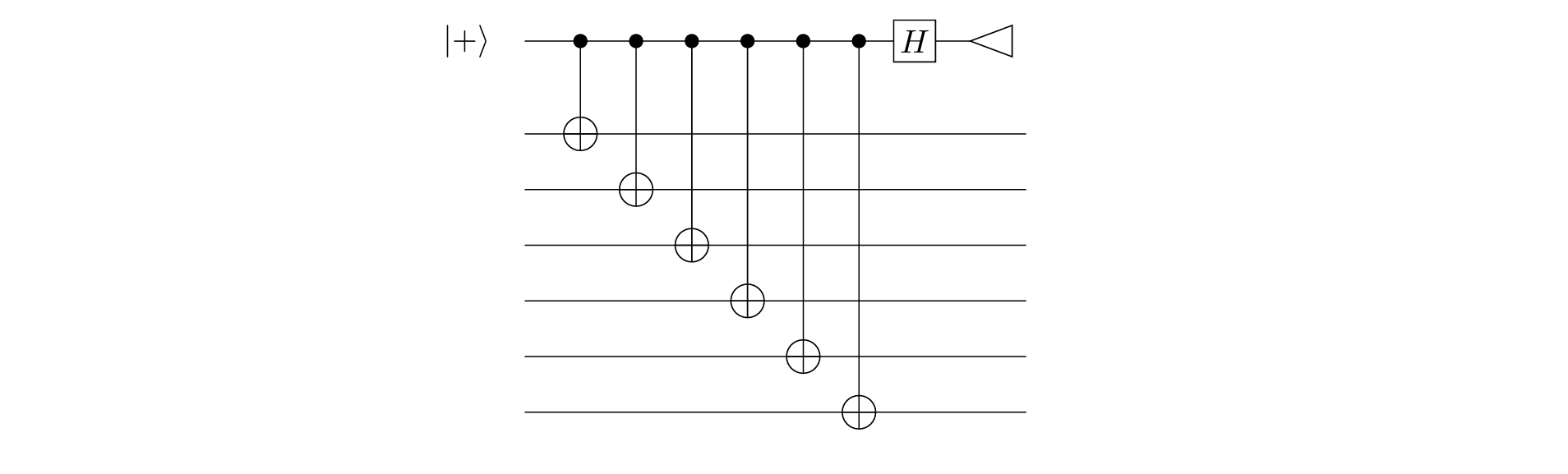
此类操作称为 Pauli Measurement。这启发我们已经有了一族码字 $C = \{|\psi_L\rangle\}$,要构造一个 QECC,可以采取以下范式:
- 找到 Pauli 群中,全体保持码字不变的元素 $S = \{\mathcal{P}\in P_n : \forall |\psi_L\rangle\in C, \mathcal{P}|\psi_L\rangle = |\psi_L\rangle\}$。
- Syndrome 以 $S$ 中各元素的特征值来表示,这可以通过 Pauli Measurement 来得到。
- 找到每一种 Syndrome 对应了何种错误。
上述 $S$ 便是所谓的 Stabilizer。
定义 3.1(Stabilizer). 一组码字 $C := \{|\psi_L\rangle\}$ 的稳定子集合定义为
$$
S = \{\mathcal{P}\in P_n : \forall |\psi_L\rangle\in C, \mathcal{P}|\psi_L\rangle = |\psi_L\rangle\}
$$
另一方面,只要给出了一组 stabilizer,这组 stabilizer 的不变子空间之交集便给出了一组合法的码字。
这个范式以下述定理之故比直观看起来更为高效:
定理 3.1. $S$ 满足以下条件:
- $-\mathcal{I}\notin S$;
- $S$ 是有限阿贝尔群。
证明. 1 显然成立。视 $P_n$ 为集合 $C$ 上的作用可见,$S$ 无非是 $C$ 中全体元素的稳定子群之交集,故必然是群。这里着重证明它是阿贝尔群。
回忆 Pauli 群的重要性质。Pauli 群中的元素只有特征值 $\pm 1$,且互相之间或者对易,或者反对易(注意 $\mathcal{I}$ 和 $\mathcal{X}, \mathcal{Y}, \mathcal{Z}$ 对易,$\mathcal{X}, \mathcal{Y}, \mathcal{Z}$ 互相反对易)。因此对于任意的 $\mathcal{M}_1, \mathcal{M}_2\in S$,有或者 $[\mathcal{M}_1, \mathcal{M}_2] = 0$,或者 $\{\mathcal{M}_1, \mathcal{M}_2\} = 0$。只需排除后者。
首先观察到对于任意的 $|\psi_L\rangle\in C$ 有 $[\mathcal{M}_1, \mathcal{M}_2]|\psi_L\rangle = |\psi_L\rangle - |\psi_L\rangle = 0$,然而若 $\{\mathcal{M_1}, \mathcal{M}_2\} = 0$,则 $[\mathcal{M}_1, \mathcal{M}_2] = 2\mathcal{M}_1\mathcal{M}_2$ 得 $[\mathcal{M}_1, \mathcal{M}_2]|\psi_L\rangle = 2|\psi_L\rangle$ 导出矛盾。
因此根据有限生成阿贝尔群的分解定理,我们只需对 $S$ 的生成元做 Pauli Measurement 即可。那么,如果一个码字集合 $C$ 的 Stabilizer 是 $S$,它能够纠正何种错误?显而易见,如果 Syndrome 测出来全是 $1$,即 $\mathcal{E}|\psi_L\rangle$ 是所有 stabilizer 的特征值为 $1$ 的特征向量,则没法纠正这种错误。这蕴含 $\mathcal{S}\mathcal{E}|\psi\rangle = \mathcal{E}|\psi\rangle = \mathcal{E}\mathcal{S}|\psi\rangle$,即 $\mathcal{E}$ 和 $\mathcal{S}$ 可交换。综上所述,此纠错码不能纠正的错误无非是 $S$ 的中心化子群,总结成如下定理:
定理 3.2. 若一个纠错码的 Stabilizer 是 $S$。$S$ 的中心化子群是 $N(S) := \{\mathcal{E}\in P_n : \forall \mathcal{S}\in S, [\mathcal{E}, \mathcal{S}] = 0\}$(不知道为何这里记号是 $N(S)$ 而非 $C(S)$)。该纠错码不能纠正的错误集合为 $N(S)\setminus S$。
证明. 前文之述备矣。注意我们从集合中刨掉了 $S$,因为其中的元素不会改变码字,故难以称得上“错误”。
另外还需要区分不同的错误。如果两个错误具有相同的 Syndrome,那么我们也无法纠正之。事实上,我们有:
定理 3.3. 一个纠错码可以纠正 $E\subseteq P_n$ 中的错误,当且仅当
$$
\forall \mathcal{E}, \mathcal{F}\in E,\qquad \mathcal{E}^\dagger \mathcal{F}\notin N(S)\setminus S
$$
证明. 显然如果 $\mathcal{E}, \mathcal{F}$ 有相同的症状,则 $\mathcal{E}^\dagger \mathcal{F}$ 有平凡的症状(所有特征值都是 $1$)。而如果 $\mathcal{E}^\dagger \mathcal{F}\in S$,则该错误可以通过同一种方式纠正。
Remark. 这里显然就显然在若 $[\mathcal{E}, \mathcal{S}] = 0$ 则 $[\mathcal{E}, \mathcal{S}^\dagger] = 0$,对于反对易性也有相同结论。读者不妨自行补充论证,此外需要时刻记住 $\mathcal{S}|\psi_L\rangle = |\psi_L\rangle$ 和 Pauli 群中元素要么对易要么反对易。
现在我们完全建立了纠错码和可纠正的错误之间的桥梁。仿照经典编码理论的定义,我们定义
定义 3.2. 称 ${S}$ 是某纠错码的 Stabilizer。记该纠错码的码距为
$$
\min \{\mathrm{wt}(\mathcal{G}) : \mathcal{G}\in N(S) \setminus S\}
$$
如果一个纠错码使用 $n$ 个物理比特编码了 $k$ 个逻辑比特,其码距为 $d$,则该纠错码称为一组 $[[n, k, d]]$-码。
由定理 3.3 立即知道,一个纠错码能纠正权重不超过 $t$ 的错误当且仅当 $d\geq 2t + 1$。
典型的纠错码
Shor Code
Shor Code 是 Shor 于 1995 年提出的一种量子纠错码。其定义为
$$
\begin{aligned}
|0_L\rangle = \frac{1}{2\sqrt 2}(|000\rangle + |111\rangle)(|000\rangle + |111\rangle)(|000\rangle + |111\rangle) \\
|1_L\rangle = \frac{1}{2\sqrt 2}(|000\rangle - |111\rangle)(|000\rangle - |111\rangle)(|000\rangle - |111\rangle)
\end{aligned}
$$
本质上,这就是把 phase-flip code 的三个物理比特都用 bit-flip code 编码。则该编码的 Syndrome 和对应的纠错可以通过以下方法完成:
- $\mathcal{X}$ Error. 查看第 $1, 2$、$2, 3$、$4, 5$、$5, 6$、$7, 8$、$8, 9$ 位的奇偶性。
- $\mathcal{Z}$ Error. 查看第 $1, 2$、$2, 3$ 块的相位(用 phase-flip code 的方式)。
- $\mathcal{XZ}$ Error. 纠正了前两个问题之后立即解决。
这个检查 Syndrome 的方式对应着 Shor Code 的 Stabilizer 群的 $8$ 个生成元:
$$
\begin{matrix}
S_1: & Z & Z & & & & & & & \\
S_2: & & Z & Z & & & & & & \\
S_3: & & & & Z & Z & & & & \\
S_4: & & & & & Z & Z & & & \\
S_5: & & & & & & & Z & Z & \\
S_6: & & & & & & & & Z & Z \\
S_7: & X & X & X & X & X & X & & & \\
S_8: & & & & X & X & X & X & X & X \\
\end{matrix}
$$
Shor Code 可以纠正 $1$ 位错误,因此 $d\geq 3$。另外注意 $\mathcal{ZIIZIIZII}$ 是 $N(S)\setminus S$ 中的元素,因此 $d = 3$。综上,Shor Code 是 $[[9, 1, 3]]$-码。
Steane Code
这是一种 Hamming 码的量子推广。其定义为
$$
\begin{aligned}
|0_L\rangle = \frac{1}{2\sqrt 2}(|0000000\rangle + |1010101\rangle + |0110011\rangle + |1100110\rangle + |0001111\rangle + |1011010\rangle + |0111100\rangle + |1101001\rangle) \\
|1_L\rangle = \frac{1}{2\sqrt 2}(|1111111\rangle + |0101010\rangle + |1001100\rangle + |0011001\rangle + |1110000\rangle + |0100101\rangle + |1000011\rangle + |0010110\rangle)
\end{aligned}
$$
它有 $6$ 个 Stabilizer 生成元:
$$
\begin{matrix}
S_1: & X & X & X & X & & & \\
S_2: & X & X & & & X & X & \\
S_3: & X & & X & & X & & X \\
S_4: & Z & Z & Z & Z & & & \\
S_5: & Z & Z & & & Z & Z & \\
S_6: & Z & & Z & & Z & & Z \\
\end{matrix}
$$
由上可见,这种纠错码像 Hamming Code 一样侦测 $\mathcal{X}$ 错误和 $\mathcal{Z}$ 错误的发生位置,从而实现 $1$-qubit 的纠错。此外 $\mathcal{IIIIXXX}$ 与所有生成元都对易,因此 Steane Code 是 $[[7, 1, 3]]$-码。
Five Qubit Code
这是一种 Shor Code 提出后不久新发现的纠错码。其 Stabilizer 生成元为
$$
\begin{matrix}
S_1: & Z & X & X & Z & \\
S_2: & X & X & Z & & Z \\
S_3: & X & Z & & Z & X \\
S_4: & Z & & Z & X & X
\end{matrix}
$$
两个码字非常长,这里有一种简单的记法
$$
\begin{aligned}
|0_L\rangle = \frac 14(\mathcal{I} + S_1)\circ (I + S_2) \circ (I + S_3) \circ (I + S_4) |00000\rangle \\
|1_L\rangle = \frac 14(\mathcal{I} + S_1)\circ (I + S_2) \circ (I + S_3) \circ (I + S_4) |11111\rangle
\end{aligned}
$$
这个码的 Syndrome 如下表所示,因此也能纠正所有的 1 qubit 错误。
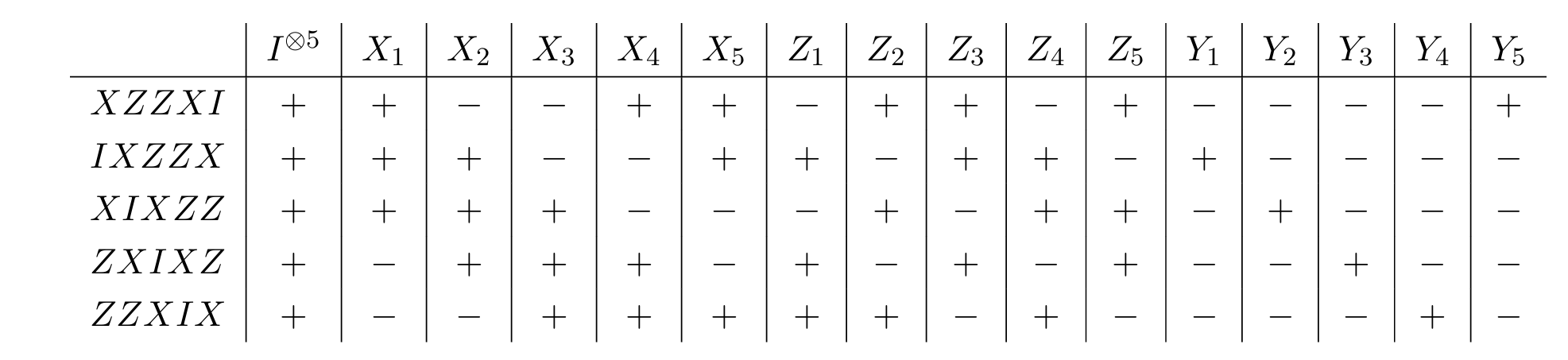
然而,$\mathcal{XIZIX}$ 和所有的生成元都对易,因此码距为 $3$。
Surface Code
以上的编码都具有固定的码距 $3$。实际上我们希望编码能随着码距 $d$ scale up。另外,为了能在具体的硬件上实现纠错码,我们希望 Stabilizer 的测量在几何上具有局部性。本人水平暂时不足以洞悉 Surface Code 构造的直觉,这里只谈论其构造。
一个表面码被组织成一个 2D 的周期性网格图,格子的每条边上都放置了一个 qubit。引自知乎的下图展示了 Surface Code 的布局:
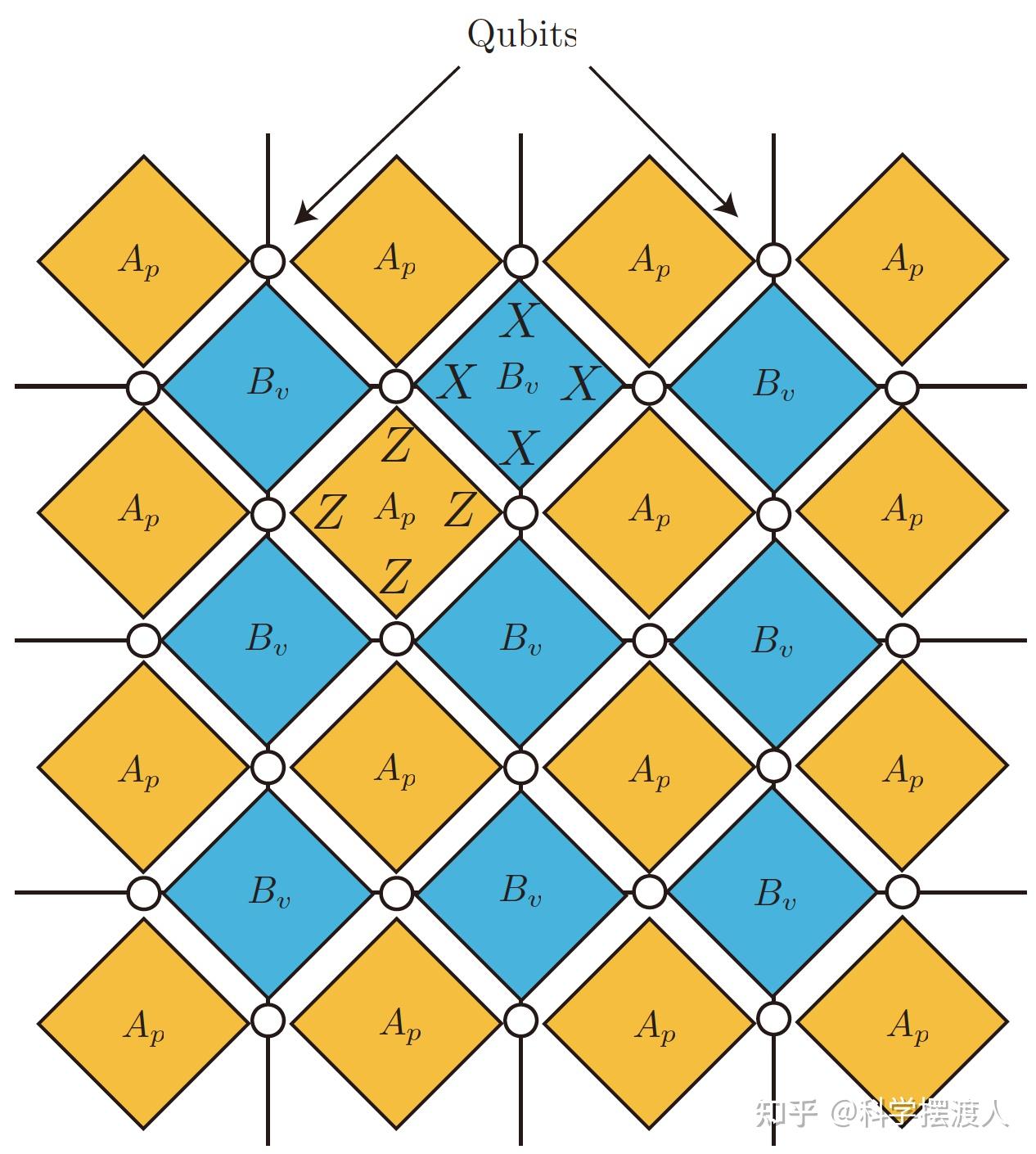
Surface Code 的 Stabilizer 分为两类。一类位于方格 $p$ 的中心,对方格上四条边上的四个 qubit 作用 $Z$ 门,称为板检查(Plaquette Check),记作 $B_p$,对应上图中的橘色板;另一类位于个格点 $v$ 上,对邻接的四个 qubit 作用 $X$ 门,称为星检查(Star Check),对应上图中的蓝色板。
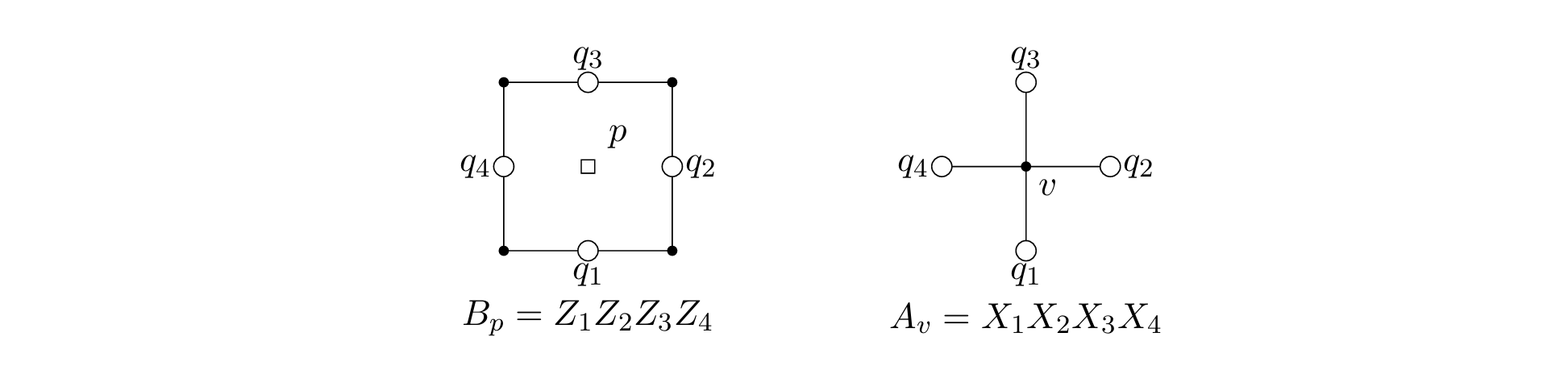
注意 $A_p$ 和 $B_v$ 相互之间都对易,因为其交于 $2$ 点或者 $0$ 点。注意,一个 $X$ error 使得与该 qubit 相邻的两个板检查测出 $-1$ 特征值,一个 $Z$ error 使得与该 qubit 相邻的两个星检查测出 $-1$ 特征值。注意,只有 $X$ 错误连接了两条相对的边的时候,这个 $X$ 错误才属于 $N(S) \setminus S$。因此只需要 $O(d^2)$ 个逻辑比特便可构造码距为 $d$ 的表面码。