Information and Entropy (6) Communication
Abstract. 本节考虑下图所示的通信模型,对 source 和 channel 部分进行建模,并给出几个与 source 的特性和 channel 的承载率相关的定理(Kraft Inequality,Gibbs Inequality,Source Coding Theorem,Noise Channel Theorem)。
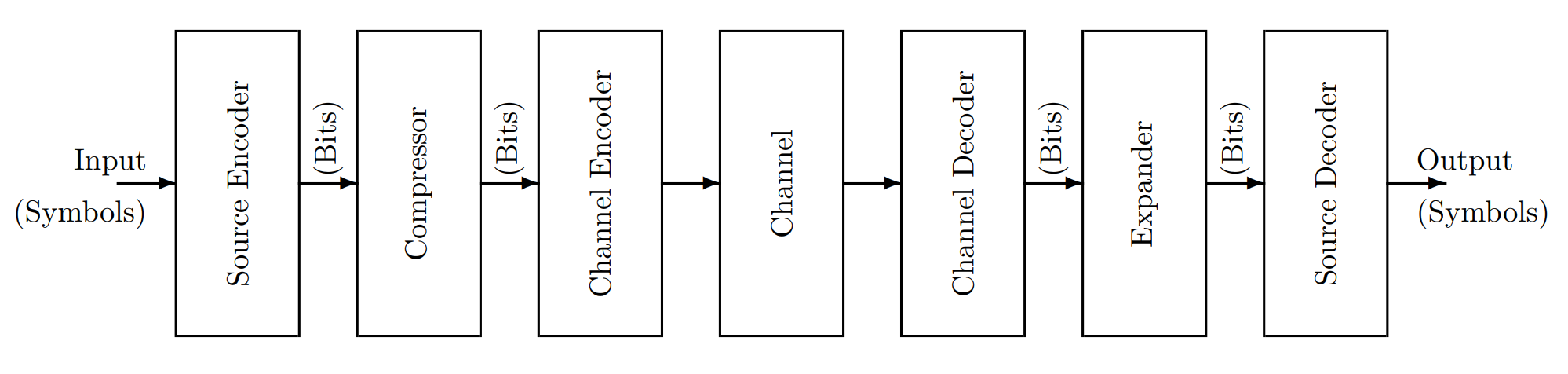
- Source Model
- Source Entropy
- Source Coding Theorem
- Channel Model
- Noiseless Channel Theorem
- Noisy Channel
- Noisy Channel Capacity Theorem
Source Model
一个 source 会以每秒 $R$ 个的速率产生字符。每一个字符是从一个有限的字符集中选出来的,选择字符 $i$ 的事件记为 $A_i$。那么存在一个从事件打到编码上的单射。称 $A_i$ 对应编码长度为 $L_i$,定长编码中 $L_i$ 均相同,变长编码中 $L_i$ 可以不同。
我们称类似于 Haffman Code 的,满足任意一个符号的编码不是另一个的前缀的编码为 prefix-condition code 或者 instantaneous code。这样的编码可以被唯一解读。
Kraft Inequality
Theorem 1.(Kraft Inequality) 对于 prefix-condition code,$L_i$ 是每个符号的编码长度,有如下的不等式
$$
\sum_{i}2^{-L_i} \leq 1
$$
Proof.
考虑 prefix-condition code 都可以画在一个 Trie 树上面。你会发现这个 Trie 树(称为 $\mathcal{T}$)对不等式左边的贡献一定小于等于一个深度和 $\mathcal{T}$ 的最大深度相等的完美二叉树(称为 $\mathcal{T}’$)。而这棵树的对不等式左边的贡献为
$$
2^{depth}\times 2^{-depth} = 1
$$
因此不等式成立。$\square$
反过来,也就是如果找到了一组 $L_i$ 满足上述不等式,那么可以构造一个满足此分布的 prefix-conditoin code。
在上一篇中我们谈到了 Haffman 编码,显然这是一个 prefix-condition code,接下来我们来证明上一篇中没有证明的这个重要结论。
Proposition. Haffman 编码的期望编码长度属于 $[I, I + 1]$,其中($p_i$ 是每个字符的出现频率)
$$
I = \sum_{i} p_i\log\left(\frac{1}{p_i}\right)
$$
Proof.
考虑计算贡献,对于一个节点,它对答案的贡献是
$$
sum_l + sum_r
$$
下界. 我们可以证明任何 prefix-condition code 的期望编码长度大于等于 $I$。
有如下重要的不等式:
$$
x + y \geq (x + y)\log(x + y) - x\log x - y\log y
$$
把每个节点的贡献用这个式子替换,除了叶子节点全部消干净了,最后只剩下了 $I$。
上界. 我们证明存在一种 prefix-condition code,其期望编码长度不超过 $I + 1$。我们构造一种满足 Kraft Inequality 的 $l_i$。
若令 $l_i = \lceil\log(1/p_i)\rceil$,那么
$$
\sum p_il_i \leq \sum p_i\left(\log\left(\frac{1}{p_i}\right) + 1\right) = I + 1
$$
而且
$$
\sum \frac 1{2^{l_i}} = \sum 2^{\lfloor\log p_i\rfloor} \leq \sum p_i = 1
$$
满足 Kraft Inequality,因此存在一个 prefix-condition code,满足其期望访问次数不超过 $I + 1$,然而根据贪心算法的原理,Haffman Code 是最优的 prefix-condition code。于是 Haffman Code 一定也符合这个上下界。
Remark. 这里的下界我们后面可以给出一个利用 Kraft Inequality 和 Gibbs Inequality 的证明。
Source Entropy
我们假设每个字符的选择都是独立的,那么下一个字符出现后我们能得到的信息量的期望就是
$$
H = \sum_i p(A_i)\log\left(\frac 1{p(A_i)}\right)
$$
这个量称为 source 的**熵(Entropy)**,单位是 bit 每个符号。也可以定义 information rate $D = H\cdot R$ 这个单位为 bit/s 的量。
Gibbs Inequality
Theorem 2.(Gibbs Inequality) 对于任意的概率分布 $p(A_i)$(满足 $\sum p(A_i) = 1$)和另一个概率分布 $p’(A_i)$(这么说可能不对劲,因为这里要求 $\sum p’(A_i)\leq 1$)都有
$$
\sum_i p(A_i)\log\left(\frac 1{p(A_i)}\right)\leq \sum_i p(A_i)\log\left(\frac 1{p’(A_i)}\right)
$$
Proof.
$$
\begin{aligned}
&\sum_i p(A_i)\log\left(\frac 1{p(A_i)}\right)- \sum_i p(A_i)\log\left(\frac 1{p’(A_i)}\right) \\
= & \sum_i p(A_i)\log\left(\frac {p’(A_i)}{p(A_i)}\right) \\
\leq & \sum_i p(A_i) \left(\frac{p’(A_i)}{p(A_i)} - 1\right) \\
= & \sum_i p’(A_i) - p(A_i) \\
\leq & 0 &\square
\end{aligned}
$$
感觉这个不等式上高中的时候肯定一眼就会证了,上大学了想半天想不明白,这是怎么回事呢(
Source Coding Theorem
定义编码的平均长度为
$$
L = \sum_i p(A_i)L_i
$$
则有
定理 3.(Source Coding Theorem)
$$
H \leq L
$$
Proof.
根据 Kraft Inequality 有
$$
\sum 2^{-L_i} \leq 1
$$
令 $p’(A_i) = 2^{-L_i}$,则
$$
L = \sum_i p(A_i)\log\left(\frac 1{p’(A_i)}\right)
$$
根据 Gibbs Inequality,$H\leq L$ 成立。$\square$
或者也可以写成速率的形式,两边都乘上产生的速率 $R$:
$$
HR\leq LR
$$
Channel Model
接下来我们对 channel 进行建模。一个 channel 会接受 input bits(可以视为一系列有限集中的事件)然后给出 output bits(可以视为与对应输入相似的另一个事件)。习惯上用 $A_i$ 表示输入事件,$B_j$ 表示输出事件。
如果一个 channel 完全根据输入给出输出而不做任何改变,称其为 noiseless。令 $W$ 表示 channel 可以跟上输入变化的最大速率(单位是 bit 每秒)。
如果字符集大小为 $n$,那么我们定义下式为 channel capacity:
$$
C = W\log_2 n
$$
如果只是通信 01 串,那么 $C = W$ 是显而易见的。
Noiseless Channel Theorem
记 input information rate 为 $D$。如果 $D\leq C$ 那么可以把信息全部传过去,否则会有 $C - D$ 的损失。把损失画下来,是一个 ReLU 函数:
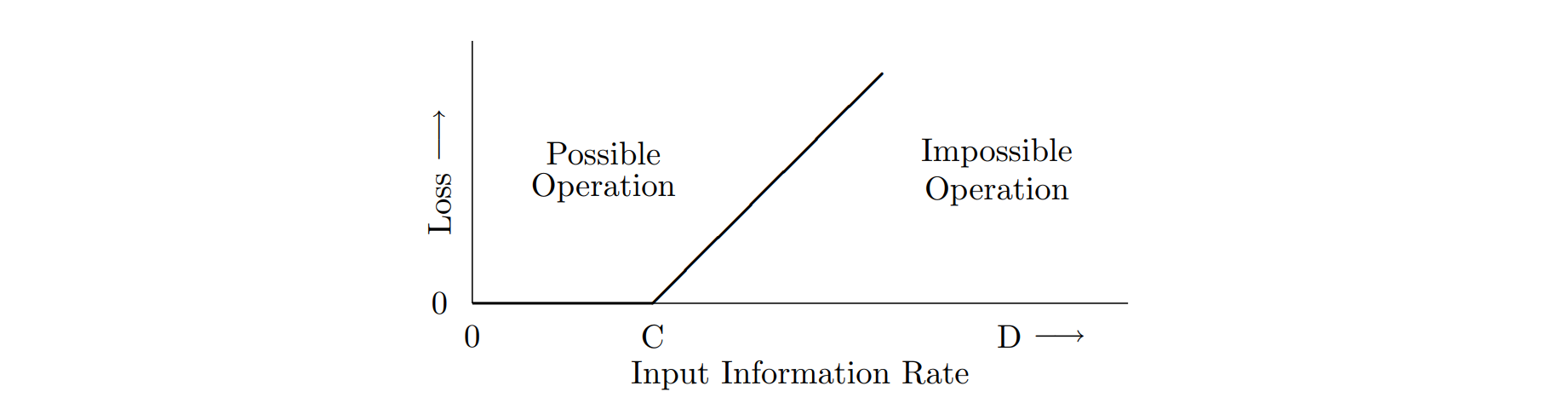
Noisy Channel
定义 Transition Probabilities:
$$
c_{ji} = P(B_j | A_i)
$$
显然有
$$
\sum_{j=1}^n c_{ji} = 1
$$
那么输出端每种字符出现的概率,依据条件概率公式为
$$
P(B_j) = \sum_{i=1}^n c_{ji}A_i
$$
想要算 $P(A_i | B_j)$ 可以用 Bayes 公式,这里略去。
最简单的 noisy channel 模型是 symmetric binary channel,如果已知它的错误率为 $\varepsilon$,那么 $\{c_{ji}\}$ 矩阵就是
$$
\begin{pmatrix} 1-\varepsilon & \varepsilon \\ \varepsilon & 1-\varepsilon \end{pmatrix}
$$
接下来我们进行一些计算。
在收到这个 channel 的 output 之前,我们对源信息的不确定度为
$$
U_1 = \sum_{i} p(A_i)\log_2\left(\frac 1{p(A_i)}\right)
$$
然后我们收到了 $B_j$,那么我们对源信息的不确定度则是
$$
U_2(B_j) = \sum_{i} p(A_i | B_j)\log_2\left(\frac 1{p(A_i | B_j)}\right)
$$
那么我们获得的信息量的期望,称为 mutual information(中文译作互信息熵),就是
$$
M = U_1 - \sum_{j}p(B_j)U_2(B_j)
$$
接下来我们给出这东西 $\geq 0$ 的证明。
$$
\begin{aligned}
&\sum_{j}p(B_j)\sum_{i} p(A_i | B_j)\log_2\left(\frac 1{p(A_i | B_j)}\right) \\
\leq & \sum_{j}p(B_j)\sum_{i} p(A_i | B_j)\log_2\left(\frac 1{p(A_i)}\right) & \text{(Gibbs Inequality)} \\
= &\sum_{i}\sum_{j} p(B_j | A_i) p(A_i) \log_2\left(\frac 1{p(A_i)}\right) \\
= &\sum_{i}p(A_i) \log_2\left(\frac 1{p(A_i)}\right)
\end{aligned}
$$
经过简单的推式子(Bayes 公式)可以得到
$$
\begin{aligned}
M &= \sum_{i} p(A_i)\log\left(\frac 1{p(A_i)}\right) - \sum_{j} p(B_j) \sum_{i} p(A_i | B_j) \log\left(\frac 1{p(A_i | B_j)}\right) \\
&= \sum_{j} p(B_j)\log\left(\frac 1{p(B_j)}\right) - \sum_{i} p(A_i) \sum_{j} p(B_j | A_i) \log\left(\frac 1{p(B_j | A_i)}\right) \\
\end{aligned}
$$
这样的对称性也说明了它被称为 mutual information 的道理。从统计上来讲,这个量可以用来衡量输入段和输出端的相关程度。
Example.
对于一个 symmetric binary channel,它的 mutual information 关于 $\varepsilon$ 的函数图像为
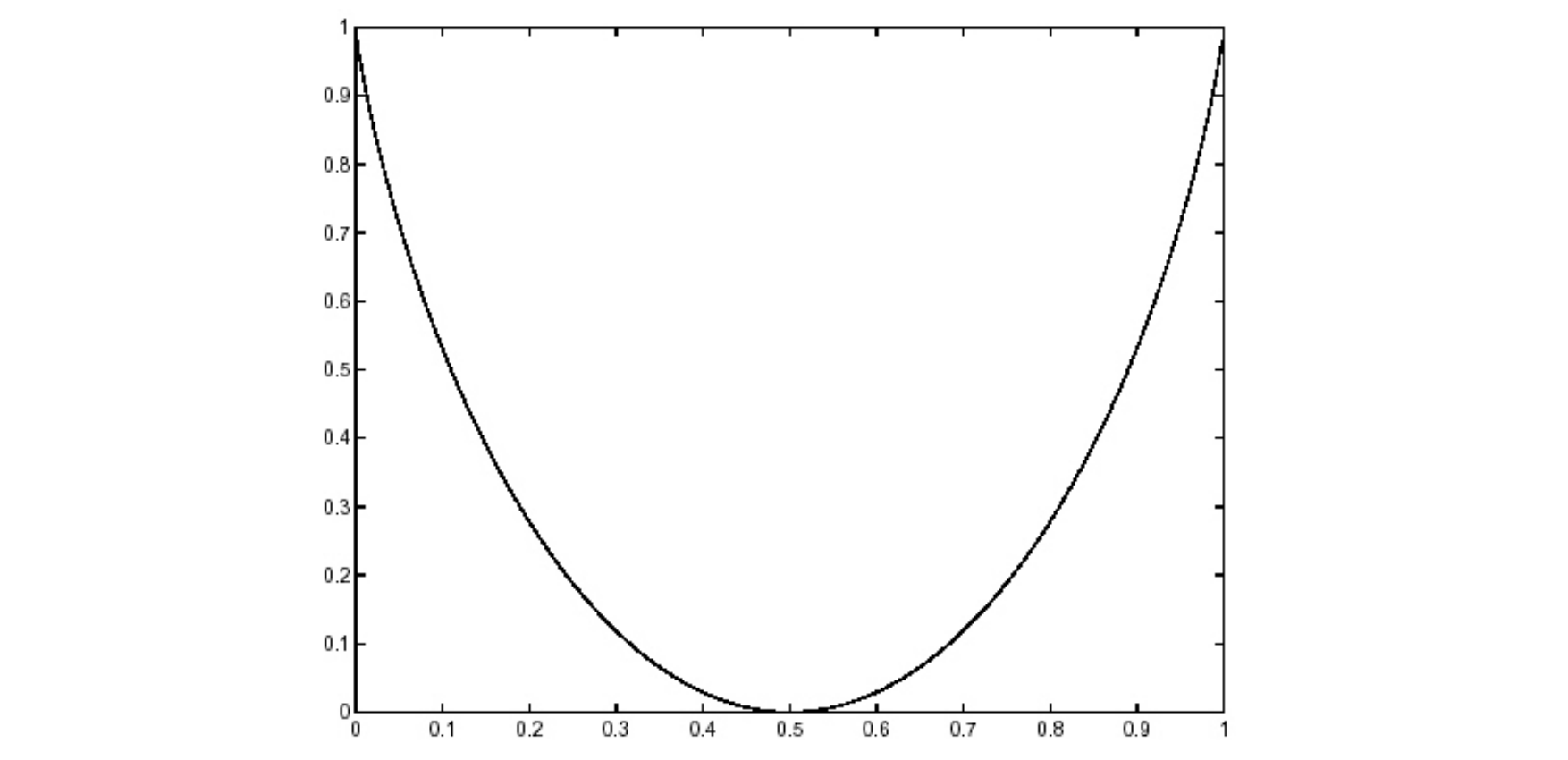
这个图显示如果错误率为 $0.5$,那么你没法得到任何信息。事实上用 $P(AB) = P(A)P(B)$ 检验,也可以发现输入端和输出端是独立的,确实相关程度为 $0$。
Noisy Channel Capacity Theorem
由于一个 channel 的 mutual information 除了取决于 channel 的 Transition Probabilities,还依赖于 source 的输出概率,所以我们在计算 capacity 的时候,一般取可能的最大值,即定义一个 noisy channel 的 capacity 为
$$
C = M_{max} W
$$
Noisy Channel Capacity Theorem,也称为 Shannon 第二定理(有噪信道编码定理),表述如下:
Theorem 4.(Noisy Channel Capacity) 如果一个输入的 information rate 为 $D$,channel capacity 为 $D$,如果 $D < C$ 那么存在一种编码方式来达到任意小的误码率。
感觉这个比较抽象,不知道抄对没有,讲义也没有给证明。据说证明只给出了存在性,没有构造。改天可以看一眼。