Revision | 信息科学中的物理学(上)热学(和一点统计力学)
Abstract. 一些热学和统计力学的复习资料,参考资料是程守洙, 江之永. 普通物理学(第七版)上册和若干课件。
学的一坨屎,这篇文章完全不能看。
基本概念
气体处于平衡态:在不受外界影响的条件下,无论初始状态如何,系统的宏观性质在充分长时间后不再发生变化的状态。可以细分为热学平衡、力学平衡、化学平衡。平衡是动态平衡,存在涨落。
需要注意稳定态和平衡态不同,比如一个高温热源和一个低温热源中间连一根管子,充分长时间之后温度分布不变,但这不是平衡态。
准静态过程 一个变化过程经过的一系列中间过程都无限接近于平衡态。
热力学第零定律 如果两个物体都和第三个物体处于平衡状态,则它们彼此处于平衡状态。
处于热平衡态的两个系统有一个属性数值相等,这个属性称为温度。热力学第零定律可以说是温度计的原理。
热量($Q$) 转移的热能。
热容 $C = \mathrm{d}Q / \mathrm{d}T$,单位质量的热容称为比热容。
状态参量 描述一个平衡态需要的一些参数,如 $p, V, T$。状态参量之间的函数关系称为物态方程。对于理想气体(实际上是压强趋于 $0$ 的极限),有
$$
pV = \frac mM RT
$$
分子的微观模型基于下面几条力学假设:
- 分子可以视为质点。
- 除了碰撞之外忽略分子相互作用。
- 接受经典力学规律,碰撞视为弹性碰撞。
- 一般忽略分子重力。
以及如下统计假设:
- 分子数密度 $n$ 分布均匀。
- 相同速率的分子中,沿各方向运动的概率相等。
统计假设 2 翻译成数学语言,可以写作如下两个公式:
$$
\begin{aligned}
&\overline{v_x} = \overline{v_y} = \overline{v_z} = 0 \\
&\overline{v_x^2} = \overline{v_y^2} = \overline{v_z^2} = \frac 13 \overline{v^2}
\end{aligned}
$$
理想气体压强 考虑一个长方体容器 $l_1 \times l_2 \times l_3$,其中有 $N$ 个质量为 $m_0$ 的同类分子,数密度为 $n$,推导压强公式。
Solution.
考虑 $l_2\times l_3$ 面,设有一个分子速度为 $\vec{v}_i$。其撞击该面,冲量为
$$
I_i = 2mv_{ix}
$$
碰撞时间间隔为 $\dfrac{2l_1}{v_{ix}}$。注意这里如果考虑其他分子的碰撞,根据动量守恒,会发生速度交换,因此“反弹”等价于“擦肩而过”。因此一定时间内的总冲量为
$$
F_i\Delta t = \frac{\Delta t v_{ix}}{2l_1}\times 2mv_{ix}
$$
故该面压强为
$$
p = \frac{1}{l_2l_3}\sum_{i=1}^N F_i = \frac{1}{l_1}\sum_{i=1}^n m_0v_{ix}^2 = nm_0\overline{v_x^2} = \frac 13nm_0\overline{v^2}
$$
最后一个等号用到了统计假设。
得到理想气体压强压强公式
$$
p = \frac 13 nm_0\overline{v^2}
$$
结合平均动能为
$$
\overline{\varepsilon_k} = \frac 12 m_0 \overline{v^2}
$$
可以改写为
$$
p = \frac 23n\overline{\varepsilon_k}
$$
考虑理想气体方程用数密度形式来写,有
$$
p = nkT = \frac 23n\overline{\varepsilon_k}
$$
即
$$
\overline{\varepsilon_k} = \frac 32 kT
$$
因此温度实际上表征分子热运动的平均动能。
方均根速率 定义(注意不是 $v$)
$$
v_{rms} = \sqrt{\overline{v^2}}
$$
则
$$
\overline{\varepsilon_k} = \frac 12 m_0\overline{v^2} = \frac 32 kT \Rightarrow v_{rms} = \sqrt{\frac{3kT}{m_0}} = \sqrt{\frac{3RT}{M}}
$$
能均分定理 在温度为 $T$ 的平衡态下,每个分子均有相等的平均动能,大小均为 $kT / 2$。
因此我们得到($i$ 为分子的自由度)
$$
\overline{\varepsilon} = \frac i2 kT
$$
实际上是把统计假设应用到转动和振动上面去。具体地,分子的平均总能量可以这样计算:
$$
\overline{\varepsilon} = \frac 12(t + r + 2s)kT
$$
这里 $t, r, s$ 分别指平动,转动,振动自由度,$2s$ 是因为平均振动动能等于平均弹性势能,此外按照理想气体的微观模型,没有其他的势能。
气体的内能定义为所有分子热运动动能和相互作用势能的总和,理想气体中只考虑平均动能。有
$$
E = \frac mM \frac i2 RT
$$
统计力学观点
速率分布律
速率位于 $v\sim v + \mathrm{d}v$ 范围内的概率记为 $f(v)\mathrm{d}v = \mathrm{d}N / N$。
麦克斯韦速率分布率
$$
f(v) = 4\pi \left(\frac{m_0}{2\pi kT}\right)^{\frac 32} \exp\left(-\frac{m_0v^2}{2kT}\right)v^2
$$
可以用来推导三个经典的统计量:
$$
\begin{aligned}
&\overline{v} = \int_0^\infty vf(v)\mathrm{d}v \\
&v_{rms} = \left(\int_0^\infty v^2f(v) \mathrm{d}v\right)^{\frac 12}
\end{aligned}
$$
以及最概然速率,这里需要求导求到极值点
$$
v_p = \sqrt{\frac{2kT}{m}}
$$
注意最概然速率对应的动能并非最概然动能。
验证.
设速率平方的分布律为 $f_2(\epsilon)$。那么
$$
f_2(\varepsilon)\mathrm{d}\varepsilon = \int_{\varepsilon}^{\varepsilon + \mathrm{d}\varepsilon} f(\sqrt{\varepsilon})\mathrm{d}\sqrt{\varepsilon}
$$
根据积分中值定理,这东西等于
$$
\begin{aligned}
&f(\sqrt{\varepsilon})\mathrm{d}\sqrt\varepsilon \\
=&f(v) = 2\pi \left(\frac{m_0}{2\pi kT}\right)^{\frac 32} \exp\left(-\frac{m_0\varepsilon}{2kT}\right)\varepsilon^{\frac 12}\mathrm{d}\varepsilon
\end{aligned}
$$
因此
$$
f_2(\varepsilon) = 2\pi \left(\frac{m_0}{2\pi kT}\right)^{\frac 32} \exp\left(-\frac{m_0\varepsilon}{2kT}\right)\varepsilon^{\frac 12}
$$
求导可以得到
$$
\varepsilon_p = \frac{kT}{m}
$$
并非直接平方的结果。
Maxwell-Boltzman 分布
以下是统计力学的唯一基本假设。
等概率原理 处于平衡态的孤立系统中,各个可能的微观态出现的概率相等。
这一节说老实话没怎么学懂。后面有很多非常难绷的近似。我们放一张图来说明
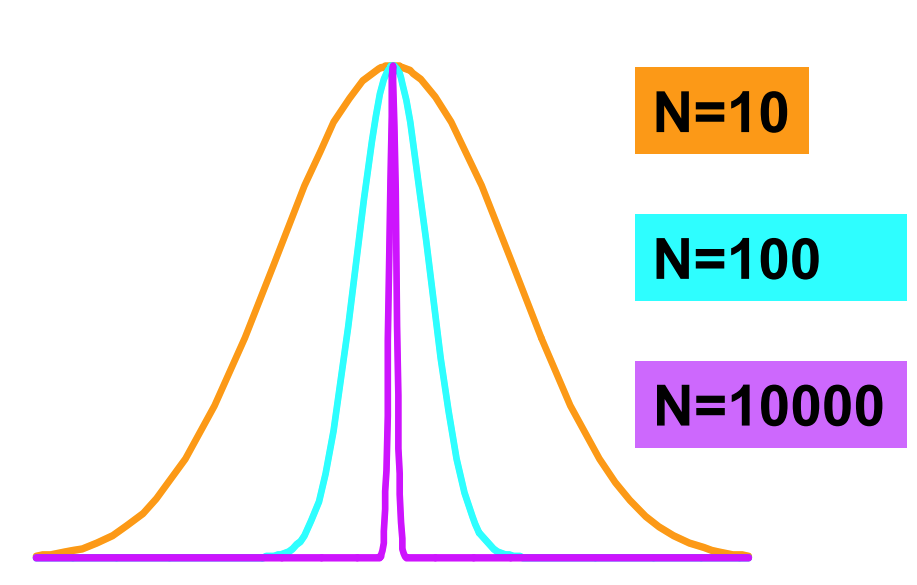
可以看到在粒子数目充分多的时候,我们可以用最概然分布来代表宏观状态,其他分布出现的概率可以忽略不记。
假设总粒子数为 $N$,系统总能量为 $E$,每个能级对应的能量为 $E_i$,粒子数为 $n_i$,我们推导最概然分布。
Derivation(Sketch).
根据基本假设可以总结出如下条件极值问题
$$
\mathrm{maximize~} W = \frac{N!}{\prod n_i!} \quad \mathrm{s.t.} \quad
\begin{cases}
\sum n_i = N \\
\sum E_i n_i = E
\end{cases}
$$
简便起见我们计算 $\ln W$,并使用斯特林近似。
$$
\begin{aligned}
\ln W &= \ln N! - \sum \ln n_i! \\
&= N\ln N - N - \sum(n_i\ln n_i - n_i) \\
&= N\ln N - \sum n_i\ln n_i
\end{aligned}
$$
引入拉格朗日乘子
$$
F = \ln W - \alpha (N - \sum n_i) - \beta(E - \sum E_in_i)
$$
得到极值条件 $\partial F / \partial n_i = 0$ 也就是 $-\ln n_i - \alpha - \beta E_i = 0$。
因此
$$
n_i = \exp(-\alpha - \beta E_i)
$$
于是概率分布为(有所约分)
$$
P(i) = \frac{n_i}{N} = \frac{\exp(-\beta E_i)}{\sum \exp(-\beta E_j)}
$$
然后 $\beta$ 的求解就非常难绷了,需要引入一些配分函数,然后主播不会了。总之可以得到 $\beta = 1 / kT$。
Maxwell-Boltzman 分布 平均粒子数按能量的分布满足
$$
\overline{n}_E = Ae^{-\frac{E}{kT}}
$$
注意这里能量等于动能加势能。且概率分布必须满足归一率,需要用 $\sum n_E / N = 1$ 凑出 $A$。
推导一定温度下,重力场中粒子的分布密度。
Solution.
等温条件下,近似认为粒子运动速率一定。因此能量只和高度有关。
因此
$$
n(z) = A \mathrm{e}^{-\frac{mgz}{kT}}
$$
用归一化求出常数 $A$ 即可。实际上这个 $A$ 就是零势能面上的分子数 $n_0$。如果已知这个量,这个公式还可以写成
$$
n(z) = n_0 \mathrm{e}^{-\frac{mgz}{kT}}
$$
结合 $p=nkT$ 可以得到气压分布
$$
p(z) = p_0\mathrm{e}^{-\frac{mgz}{kT}}
$$
可以用 MB 分布推导能均分定理,本质上是如果能量可以写成若干个平方项的和,每个平方项中,变量可以等概率地取任意值,那么每个平方项的能量都是 $\frac 12 kT$。
熵
Boltzman 关系
$$
S = k\ln W
$$
其中 $W$ 为微观状态数。
比如说在 $W = (N!) / (\prod n_i!)$ 有
$$
\begin{aligned}
S &= kN\ln N - k\sum n_i\ln n_i \\
&= -k/N\sum\frac{n_i}{N}\ln\left(\frac{n_i}{N}\right) \\
&= -k/N\sum P_i\ln P_i
\end{aligned}
$$
最大熵原理 系统的平衡态分布对应熵最大的分布。
可以用来推导温度的统计力学定义。
Derivation(Sketch).
假设第一个系统能量为 $E_1$,第二个系统能量为 $E_2$,熵分别为 $S_1, S_2$,有 $E = E_1 + E_2$(能量守恒)。
根据最大熵原理,两系统平衡时
$$
\frac{\mathrm{d}S}{\mathrm{d}E_1} = 0 \Rightarrow \frac{\mathrm{d}S_1}{\mathrm{d}E_1} = \frac{\mathrm{d}S_2}{\mathrm{d}E_2}
$$
可以定义平衡态下这个相等量为统计力学意义下的温度:
$$
T = \left(\frac{\mathrm{d}S}{\mathrm{d}E}\right)^{-1}
$$
取倒数是为了保持能量从高温传到低温的习惯。
$$
T = \left(\frac{\mathrm{d}S}{\mathrm{d}E}\right)^{-1}
$$
形象的理解就是,为了达到平衡,要熵最大。考虑 $S-E$ 图,一个斜率小,一个斜率大,那么能量从斜率小的转移到斜率大的可以使熵的和变大。
热力学观点
基本概念
改变内能的方式:传热(微观功)和做功(宏观功)。
考虑准静态过程:有
$$
\mathrm{d}A = pS\mathrm{d}l = p\mathrm{d}V
$$
因此做功就是 $p-V$ 图曲线下面积。
热力学定律
除热力学第零定律之外有如下几条:
热力学第一定律.
$$
\delta Q = \mathrm{d}E + \delta A
$$
这里的 $\delta Q$ 是因为 $Q$ 是一个状态函数,写成了全微分形式。
这指出第一类永动机(不吸热而能向外放热 / 做功的机器)不存在。
基于此定律可以推导四类准静态过程相关量。
等体过程 满足 $\mathrm{d}V = 0$。
方程为 $\frac pT = C$。
显然 $\delta A = 0, \delta Q = \mathrm{d}E$。
定体热容
$$
C_{V, m} = \frac{\delta Q}{\frac mM \cdot \mathrm{d}T} = \frac{\mathrm{d}\frac mM \frac i2 RT}{\frac mM \mathrm{d}T} = \color{blue} \frac{i}{2}R
$$
等压过程 满足 $\mathrm{d}p = 0$。
方程为 $\frac VT = C$。
显然 $\delta Q = \mathrm{d}E + p\mathrm{d}V$。
定压热容
$$
C_{p, m} = \frac{\delta Q}{\frac mM \cdot\mathrm{dT}} = \frac{\mathrm{d}E + p\mathrm{d}V}{\frac mM \cdot\mathrm{dT}} = \frac{\mathrm{d}\frac mM\frac i2 RT + \mathrm{d}\frac mM RT}{\frac mM \mathrm{d}T} = \color{blue}\frac{i + 2}{2}R
$$
定义比热容比 $\gamma = C_{p, m} / C_{V, m} = \frac{i + 2}i$。
等温过程 $\mathrm{d} T = 0$。
方程为 $pV = C$。
满足 $\mathrm{d}E = \frac i2 R\mathrm{d}T = 0$,也就是说吸收的热全部用于做功。
绝热过程 满足 $\delta Q = 0$。
方程并不显然,我们需要进行一些推导。
Derivation.
$$
\mathrm{d}E + \delta A = 0\Rightarrow \frac mM \frac i2 R\mathrm{d}T + p\mathrm{d}V = 0
$$
这里 $p, V$ 均为变量,我们有
$$
p\mathrm{d}V + V\mathrm{d}p = \mathrm{d}pV = \frac mM R\mathrm{d}T
$$
这里希望得到 $p-V$ 图上的方程,因此换掉 $\mathrm{d}T$。
$$
\frac i2 (p\mathrm{d}V + V\mathrm{d}T) + p\mathrm{d}V = 0 \Rightarrow \gamma \frac{\mathrm{d}V}{V} + \frac{\mathrm{d}p}{p} = 0
$$
两边积分之后取 $\exp$ 得到方程。
$$
pV^{\gamma} = C
$$
$p, V, T$ 知二推一,因此
$$
\begin{aligned}
&TV^{\gamma - 1} = C \\
&T^{-\gamma}p^{\gamma - 1} = C
\end{aligned}
$$
至于做功直接使劲积分即可,积出来形式比较好,是
$$
-\frac mM C_{V, m} (T_2 - T_1)
$$
考虑定义热机和冷机:将热能和功互相转化的机器。
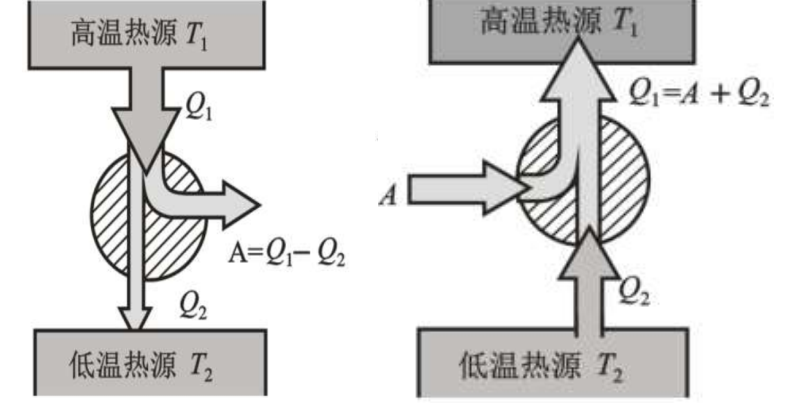
可以定义热机和冷机的效率:
$$
\begin{aligned}
\eta = \frac A{Q_1} = 1 - \frac {Q_2}{Q_1} \\
\omega = \frac{Q_2}{A} = \frac{Q_2}{Q_2 - Q_1}
\end{aligned}
$$
热力学第二定律 不存在单源热机(开尔文表述)和无功冷机(克劳修斯表述)。
单源热机和无功冷机可以双向规约,方案是显然的。
定义卡诺热机是由两个等温过程和两个绝热过程组成的循环过程。
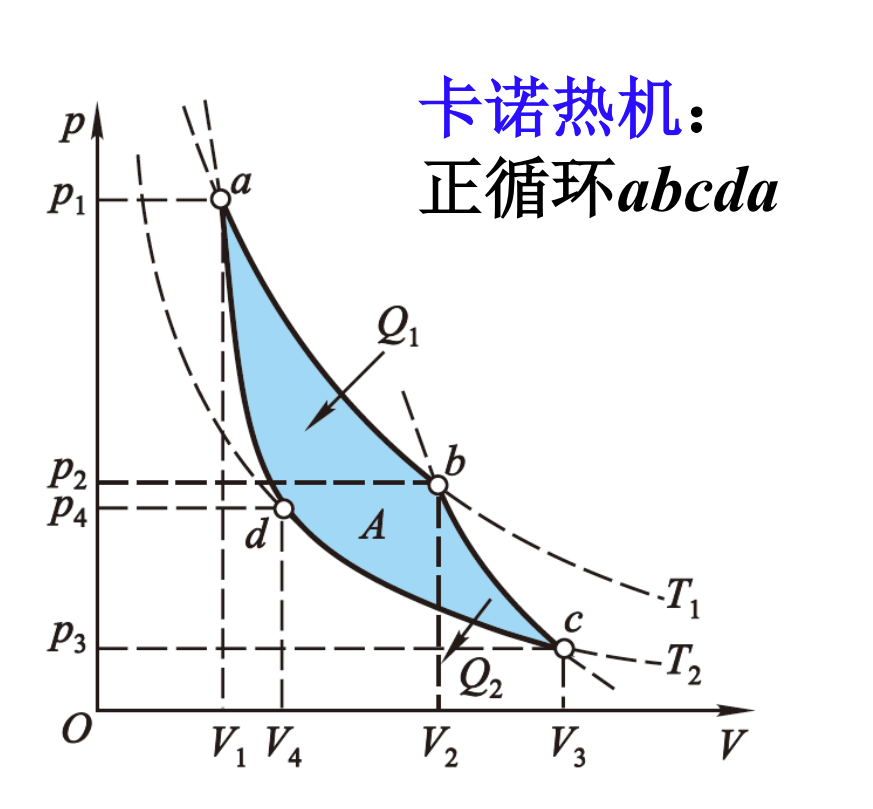
简单计算可以得到
$$
\eta = 1 - \frac{T_2}{T_1}
$$
在卡诺循环中,有($Q_2$ 是负的)
$$
\frac{Q_1 + Q_2}{Q_1} = \frac{T_1 - T_2}{T_2}
$$
可以得到
$$
\frac{Q_1}{T_1} + \frac{Q_2}{T_2} = 0
$$
对于其他可以画在 $p-V$ 图上的循环(称为可逆循环),可以将其拆分称若干个卡诺循环,得到
$$
\sum \frac{Q_i}{T_i} = 0
$$
定义克劳修斯熵:
$$
\mathrm{d}S = \frac{\delta Q}{T}
$$
将上面的式子写成积分形式,得到对于可逆过程:
$$
\oint \frac{\delta Q}{T} = 0
$$
热力学第二定律也可以写成克劳修斯不等式(对于任意循环):
$$
\oint \frac{\delta Q}{T}\leq 0
$$
计算一个可逆过程的熵变只需要用
$$
\int_1^2 \frac{\delta Q}{T}
$$
然后用上面四种常见热力学过程的性质换掉 $\delta Q$ 做积分即可。
需要注意的是对于一个不可逆过程你算不了 $\delta Q$ 之类的东西。但是熵是一个状态量,你只需要构造一个过程连接初末状态即可。
熵增加原理
$$
\mathrm{d}S \geq 0
$$
取等当且仅当过程可逆。这相当于给出了自发过程的方向和限度。
绷不住了不想看了。
背几个公式,然后看往年题。
其他东西
平均自由程
这里有一个非常抽象的近似:视为其他分子不动,一个分子以平均相对速率运动。假设分子数密度为 $n$。
碰撞截面大小:$\sigma = \pi d^2$
碰撞频率 $\overline{Z} = \pi d^2\overline{v}_r n$,这里的 $\overline{v}_r$ 是平均相对运动速率。
可以证明 $\overline{v}_r = \sqrt 2 \overline{v}$,怎么证的主播并不知道。所以 $\overline{Z} = \overline{Z} = \sqrt 2\pi d^2\overline{v} n$。
于是平均自由程为
$$
\overline{\lambda} = \frac{\overline{v}}{\overline{Z}} = \frac{1}{\sqrt 2\pi dn}
$$