Revision | 经济学原理
本文假设读者掌握 Lagrange Multiplyer、Karush-Kuhn-Tucker Condition 之类的分析手段。
经济学的思维方式
【FIXME】
微观经济学
偏好与选择
消费者对于可能做出的各种选项有自己的偏好。在具有现实意义的讨论范围内,不妨考虑选项构成一个基数不超过 $|\mathbb{R}|$ 集合 $\mathcal{X}$,偏好就是 $\mathcal{X}$ 上的一个二元关系 $\preceq$。对于一个理性的消费者,其偏好应当是 $\mathcal{X}$ 上的一个全序:
定义 2.1.1(理性的偏好). 称一个消费者在消费集 $\mathcal{X} \subseteq \mathbb{R}_{+}^L$ 上的偏好 $\preceq$ 是理性的,当且仅当:
- (完备性). $\forall x, y\in \mathcal{X}, x \preceq y \vee y\preceq x$。
- (自反性). $\forall x\in \mathcal{X}, x\preceq x$。
- (传递性). $\forall x, y, z, x\preceq y \wedge y \preceq z \rightarrow x \preceq z$。
理性的消费者如何在这个一般的全序集上的选择让人无从下手。一个便利的方法是将偏好可视化为效用,因为采用某些集合论手段可以证明
定理 2.1.1. 对于任意理性的偏好关系,存在一个效用函数 $u: \mathcal{X}\rightarrow \mathbb{R}$ 使得
$$
\forall x, y\in \mathcal{X}, \quad x\preceq y \leftrightarrow u(x) \preceq u(y)
$$
直觉上来说,效用就是对消费者的欲望的满足程度的量化。再对偏好附加诸如连续性之类的假设,可以推出 $u$ 要么是单调递增的(GOODS,多多益善),要么是单调递减的(BADS,少少益善)。那么,“先满足较迫切的需求”是人的天性使然,因此通常对效用函数附加假设:边际效用递减,即效用函数 $u$ 是连续的上凸函数。效用函数的梯度称为边际效用,记作 $MU = \nabla u$。
当然,获得效用可能需要付出成本。根据“物以稀为贵”的直觉,一般对成本函数附加假设:边际成本递增,即成本函数 $c$ 是下凸函数,记作 $MC = \nabla c$
经过以上工具准备,我们可以开始研究以下问题。
问题 2.1.1(无约束的最优资源配置). 考虑成本函数 $c$ 和效用函数 $u$。消费者的收益可用
$$
u(\boldsymbol{x}) - c(\boldsymbol{x})
$$
刻画。如何最大化此函数?
这是一个上凸函数,其最大值点的充分必要条件是
$$
\nabla (u(\boldsymbol{x}) - c(\boldsymbol{x})), \qquad \text{i.e. } MU(\boldsymbol{x}) = MC(\boldsymbol{x})
$$
这说明最优资源配置的基本原则是边际收入等于边际成本。
问题 2.1.2(有约束的资源分配问题). 现在考虑效用函数 $u$ 和资源约束 $g(\boldsymbol{x})\leq 0$。其中 $g(\boldsymbol{x})$ 形似某种成本,理应是一个下凸的函数。不妨考虑下面的特例:“多多益善”导致我们先验地知道了在 $g(\boldsymbol{x}) = 0$ 这条线(称为生产可行性边界)上做决策才能产生最优解。如何解优化问题
$$
\max u, \text{ s.t. } g = 0
$$
此时 Langrange multiplyers 的驻点条件给出此时必须有
$$
\nabla u = \lambda \nabla g
$$
即无差异曲线和生产可能性边界相切。
不妨考虑只有两种产品($L = 2$,两个产品分别为 $x, y$),此时我们有更直观的理解。此时,上述公式等价于
$$
\frac{\partial_x u}{\partial_y u} = \frac{\partial_x g}{\partial_y g}
$$
上述计算中,蕴含以下概念:
- 无差异曲线. 即效用函数的等高线。
- 边际替代率. 为了保持总效用不变,拿出一单位 $x$,你愿意换几单位 $y$。
$$
MRS = \frac{MU_x}{MU_y}
$$
几何上,根据隐函数存在性定理,$MRS$ 就是无差异曲线的斜率的相反数。 - 边际转化率. 为了保持在生产可行性边界上,增加一单位 $x$,需要付出多少单位 $y$,也就是 $x$ 的机会成本。
$$
MRT = \frac{P_x}{P_y}
$$
因为这件事类似于做等价交换,一单位 $x$ 能换多少 $y$,所以用 $P_x, P_y$ 来命名 $\partial_x c$ 和 $\partial_y c$。几何上,$MRT$ 就是生产可能性边界的斜率的相反数。
这就是说,两个产品、生产可行性边界上最优效用点的充分必要条件是边际替代率等于边际转化率。
交换、分工、货币
因为资源禀赋(初始资源分配)和偏好的不同,交换可以使得每个人的处境都得到改善。交换物之间的比例称为价格。在不借助于货币的直接交换情景之下,有 $N$ 个产品交换,就有 $N(N - 1) / 2$ 个交易比价。
设有两种商品,其总量分别为 $X, Y$。交易双方的初始分配分别为 $x, y$,交易双方的效用函数分别以 $u_1, u_2$ 刻画。如果 $\nabla u_1(x, y)$ 和 $\nabla u_2(X - x, Y - y)$ 不共线,则必存在 $\lambda, \mu$,将资源配置修改为 $(x, y) + \lambda \nabla u_1 + \mu \nabla u_2$ 使得双方效用都获得改进,称为帕累托改进。若不存在帕累托改进,则称为帕累托最优。很明显,帕累托改进不唯一。全体帕累托改进的目标点,称为交易合同线。至于双方谈判到交易合同线上的哪一个帕累托最优点,则要看双方水平。
Edgeworth Box 是两个产品的可视化交换过程的重要工具,其形如下图,不言而喻。
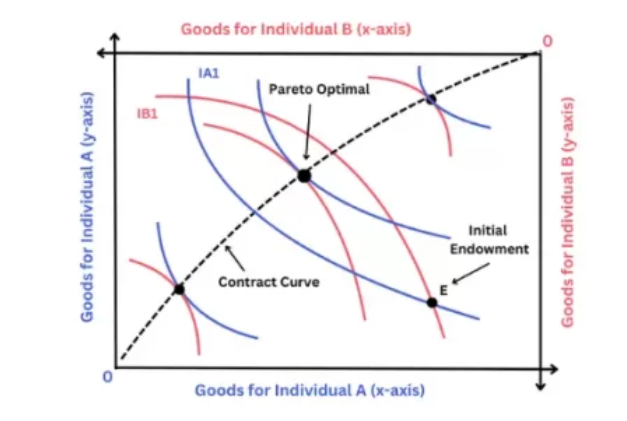
初始分配何以决定?除了资源禀赋之外,尤其是对于产品而言,分工和专业化更是重要的因素。鉴于各方对诸产品的生产能力不同,进行分工可以优化社会总产量。一方可能会因为以下两种优势之一而选择专业化于生产某一种产品:
- 绝对优势. 一个人在某种产品的生产上的绝对生产率(指仅专注于生产这一个商品的可能性边界)大于其他人;
- 相对优势. 一个人在所有产品的生产上的绝对生产率都不及其他人,但是生产某一产品的机会成本小于其他所有人。
问题 2.2.1(可贸易区间). 设 $A, B$ 两人生产 $X, Y$ 两种商品。其中 $A, B$ 生产 $X$ 的机会成本是 $OC_A(X)$ 和 $OC_B(X)$(个 $Y$ / 每单位 $X$),设 $A$ 在 $X$ 上有比较优势,双方可以发生交易的必要条件是相对价格 $\frac{P_X}{P_Y}$ 满足何种要求?
$A$ 有比较优势即 $OC_A(X) < OC_B(X)$。注意若价格 $\frac{P_X}{P_Y} \leq OC_A(X)$,则 $A$ 不如自己放弃 $Y$ 生产 $Y$ 而非找 $B$ 交换。类似地若 $\frac{P_X}{P_Y} \geq OC_B(X)$,$B$ 也不会愿意用手里的 $Y$ 去换 $A$ 的 $X$。综上所述,可贸易区间为
$$
(OC_A(X), OC_B(X))
$$
可以发现当有绝对优势的双方按照绝对优势完全专业化,将带来社会资源的偏序意义上的全面提升。若仅有相对优势,但是两商品的价格恰好又在可贸易区间之内,双方也能获得各自生产可行性边界外的资源分配。
在上方我们已经讨论过了直接交换。直接交易的一个困境是需求的巧合:交易双方之间的供需匹配比较困难(比如 $A$ 想用 $X$ 换 $B$ 的 $Y$,但是 $B$ 不一定想要 $Y$ 反而想要 $Z$ 之类)。因为此时交易的代价过高,所以大部分个体将选择自给自足而非进行交换,分工和专业化的优势无从发挥。
随着个体之间的联系变得更加紧密,充当一般等价物的货币应运而生。货币的出现,使得间接交换(交易双方至少有一方得到的东西并非为了直接使用,而是为了以后换取一些别的东西)成为可能。
消费者选择与需求曲线
在自给自足的自然经济下,生产和消费完全是一回事,生产计划完全取决于个人偏好和资源禀赋。在市场经济下,生产和消费分离,价格成为了生产选择和消费选择的协调机制。
给定收入和偏好,预算收入是消费者选择的唯一约束条件。价格是决定性因素。
单个商品的价格和购买量之间的关系,可以用需求表和需求曲线描述(前者是后者的离散版本)。需求曲线应当满足需求法则:需求量随着价格则下降而增加。
消费者剩余是指消费者宁愿付出而不愿意得不到此物的最大价格与消费者为此物实际上支付的价格之间的差异部分。若价格关于需求的函数是 $P(x)$,则购买量 $x$ 处的消费者剩余为
$$
CS = \int_0^x (P(t) - P(x))\mathrm{d}t
$$
我们现在来建立关于需求曲线、消费者剩余等概念的直觉。不妨设消费者认为该物品的效用是 $u(x)$,在这个语境下特别称为**支付意愿 $WTC$**(注意,支付意愿就是消费者眼中物品的效用,万不可将其理解为我愿意为 $x$ 个东西总共花多少钱)。那么在购买该物品时,消费者将会求解如下优化问题来决定购买多少该物品:
$$
\arg\max_x u(x) - px
$$
其解由方程 $P(x) = u’(x)$ 给出。换言之,需求曲线——定价为 $p$ 时的成交量就是上述函数的反函数。需求法则,即需求量随价格下降而增加,本质上无非是边际支付意愿(即边际效用)递减。而 $CS$ 确实就是 $u(x^*) - p(x^*)$,这由微积分基本定理立即得到。
显而易见,若改进技术导致价格减小,则消费者剩余将增加。
接下来我们考虑价格变动如何影响消费者选择。首先定义
定义 2.3.1(瓦尔拉斯需求). 表示给定收入水平和价格的条件下,最优效用对应的消费量。
$$
\boldsymbol{x}^*(\boldsymbol{p}, m) := \arg \max_{\boldsymbol{x}} u(\boldsymbol{x}) \text{ s.t. } \boldsymbol{p}\cdot \boldsymbol{x} = m
$$
定义 2.3.2(希克斯需求). 表示目标效用下,最小成本对应的消费量:
$$
\boldsymbol{h}(\boldsymbol{p}, u) := \arg \min_{\boldsymbol{x}} \boldsymbol{p}\cdot \boldsymbol{x} \text{ s.t. } u(\boldsymbol{x}) = u
$$
不妨假设 $u(x)$ 是严格凸、多多益善的,即上述两个优化都只有唯一解。则设 $u^*$ 为瓦尔拉斯需求对应的最优效用,有
$$
\boldsymbol{x}^*(\boldsymbol{p}, m^*) = \boldsymbol{h}(\boldsymbol{p}, u^*)
$$
否则你可以以小于 $m$ 的成本达到效用 $u^*$,此时多买一点任意物品使得效用变大,与 $u^*$ 最优矛盾。现在保持最优效用 $u^*$ 不变,$m^*$ 为该点处希克斯需求给出的最优解($\boldsymbol{x}\cdot \boldsymbol{p}$),在这个点处,同样的等式成立(式子中的变量只有 $p$,$u^*, m^*$ 都是恰到好处的定值)。此时对 $p_i$ 求偏导得到
$$
\frac{\partial x_j(\boldsymbol{p}, m^*)}{\partial p_i} + \frac{\partial x_j(\boldsymbol{p}, m^*)}{\partial m}x_i(\boldsymbol{p, m}) = \frac{\partial h_j(\boldsymbol{p}, u^*)}{\partial p_i} \label{slutsky}
$$
至此我们证明了
定理 2.3.1(斯勒茨基方程). 如下方程成立:
$$
\frac{\partial x_i}{\partial p_i} = \frac{\partial h_i(\boldsymbol{p}, u)}{\partial p_i} - x_i\frac{\partial x_i}{m}
$$
其中第一项成为替代效应,第二项成为收入效应。
以下是关于替代效应和收入效应的经济学直觉,以此导出替代-收入效应分解的离散版本。首先考虑消费者效用 $u(\boldsymbol{x})$,初始价格 $\boldsymbol{p}$ 下有最优消费组合 $\boldsymbol{x}^0$。现在将 $p_1$ 改为 $p_1’$,新最优组合为 $\boldsymbol{x^1}$。另外定义预算补偿线为价格变动之后使得效用水平不变的收入水平,即
$$
u(\boldsymbol{x}^c) = u(\boldsymbol{x}^0), \qquad \boldsymbol{p}’\cdot \boldsymbol{x}^c = m’
$$
则替代-收入效应分解无非是
$$
TE = x^1_1 - x^0_1 = (x^1_1 - x^c_1) + (x^c_1 - x^1_1) = SE + IE
$$
- 替代效应. 保持效用水平不变的情况下,价格变化引起的最优消费的变动。
- $SE > 0$ 总是成立。当价格下降时,消费者通常倾向于购买更多该商品。
- 收入效应. 保持新价格不变的情况下,由于实际购买力导致的消费变动。
- 若为正常品,$IE > 0$,总需求增加;
- 若为劣等品,$IE < 0$,但若 $|IE| < |SE|$,仍表现为需求增加;
- 若 $|IE| > |SE|$,则称为吉芬商品:需求量随价格上升而增加。
最后说一些有关指数。
定义 2.3.3(需求的价格弹性). 反应需求对价格变动的敏感程度,为需求变化的百分比除以价格变化的百分比,表现为如下的离散和连续形式
$$
E_d = \frac{\Delta Q / Q}{\Delta P / P} = \frac{Q’}{P’}\cdot \frac{P}{Q}
$$
这个数始终是负数。按照 $1$ 分界,绝对值大于 $1$ 的是有弹性的,小于 $1$ 的是缺乏弹性的。分界的依据是
$$
\frac{\mathrm{d}}{\mathrm{d}P} Q\cdot P = 0
$$
即,降价是否可以增收。直觉上,有
- 替代品越多,弹性越大;
- 耐久性越长,弹性越大;
- 必需品的弹性小,奢侈品的弹性大。
定义 2.3.4(需求的收入弹性). 反应需求对收入的敏感程度,为需求变化的百分比除以收入变化的百分比:
$$
E_y = \frac{\Delta Q / Q}{\Delta Y / Y} = \frac{Q’}{Y’} \cdot \frac{Y}{Q}
$$
这个值为正数,也可以按照 $1$ 分界,必需品的收入弹性小于 $1$,奢侈品的收入弹性大于 $1$,分界的依据是
$$
\frac{\mathrm{d}}{\mathrm{d}Y} \frac{PQ}{Y} = 0
$$
即增加收入,消费占比是否变化。
定义 2.3.5(真实生活费用指数、价格指数). 真实生活费用指数用于刻画不同价格下为了打到某个给定的效用水平需要的最低支出的比例:
$$
P(\boldsymbol{p}^1, \boldsymbol{p}^0, u^R) = \frac{e(\boldsymbol{p}^1, u^R)}{e(\boldsymbol{p}^0, u^R)}
$$
此处 $e(\boldsymbol{p}, u) = x(\boldsymbol{p}, u)\cdot \boldsymbol{p}$,$x$ 为瓦尔拉斯需求。
由于效用不易显示观测,一般采用以下两种价格指数:
- Laspeyres 价格指数. $LP = \frac{\boldsymbol{p^1\boldsymbol{x}^0}}{\boldsymbol{p}^0 \boldsymbol{x}^0}$;
- Passche 价格指数. $PP = \frac{\boldsymbol{p}^1 \boldsymbol{x}^1}{\boldsymbol{p}^0 \boldsymbol{x}^1}$。
发生涨价时:
- LP 分子 $\boldsymbol{p}^1\boldsymbol{x}^0 \geq e(\boldsymbol{p}^1, u^0)$,高估了真实生活费用的上升;
- PP 分母 $\boldsymbol{p}^0\boldsymbol{x}^1 \geq e(\boldsymbol{p}^0, u^1)$,低估了真实生活费用的上升。
生产和供给曲线
上一节讨论了消费者。其选择决定市场需求。本节来讨论生产者,其决定市场供给。
其中利润为销售收入减去生产成本,用以下式子刻画
$$
\pi(y) = yp - C(y)
$$
显然,价格一定时,利润最大化的条件为边际收益($MR$)等于边际成本($MC$),即 $MR(y) = p = MC(y)$。而产量 $y$ 和成本可以进一步做拆分:
- 生产函数. 给定原料 $\boldsymbol{x}$,产量 $y$ 关于 $\boldsymbol{x}$ 的函数为生产函数 $f(\boldsymbol{x})$。这个函数是上凸的,即边际产出递减。
- 固定成本和可变成本. 固定成本指和产量没有关系的成本(地租、工资、设备等);可变成本指来自产量和可变投入的成本(化肥、设备折旧等)。
根据投入同比例增加至 $\lambda$ 倍,产出是大于、小于、等于 $\lambda$ 倍分为规模报酬递增、递减、不变。对于常用的 Cobb-Douglas 生产函数
$$
f(z_1, z_2) = z_1^\alpha z_2^\beta
$$
规模报酬取决于 $\alpha + \beta$。
至此,可以研究以下问题:
问题 2.4.1(边际成本曲线和供给曲线). 供给曲线 $S(p)$ 是产量 $y$ 关于销售单价 $p$ 的函数。若生产者的目标是最大化利润,则供给曲线如何?
直接用微积分计算,可以知道供给曲线正是边际成本曲线 $MC$ 的反函数。
问题 2.4.2(最优要素投入组合). 现在产量 $y$ 取决于两种要素(如资本和劳动)的投入量,问生产出产量 $y_1$ 的最优要素投入组合如何?
将产量 $y$ 视为效用。则一个投入组合是最优的当且仅当此时的边际替代率(两要素的边际生产率之比)等于要素价格比。
当然,最后你也可以定义供给的价格弹性之类的东西,这里不再赘述。
供求与市场均衡
市场是指买卖双方进行经济交换的场所或机构,具有资源配置、价格发现、风险转移等作用。
在此类存在两方(这里是买卖双方),我们通常分析均衡:各方力量达到平衡状态,使得没有进一步的调整发生。
市场均衡 系指供给和需求之间的平衡状态,在某一价格水平下,所有的意愿需求都得到了满足,所有的意愿产出都找到了买主。此时的价格称为均衡价格,产量称为均衡产量。
短期均衡价格和均衡产量就是供给曲线和需求曲线的交点的横纵坐标。 在均衡价格下方,供小于求,在均衡价格的上方,供大于求,都没有达到平衡状态。
然而,现实中没有边际效用的量化,没有人知道供给曲线和需求曲线的交点究竟在何处,另一方面供给曲线和需求曲线也是时刻变动的。因此,市场总是处在非均衡的状态,但是通过竞价趋向均衡。简而言之供小于求时买者竞价会导致价格上调,供大于求时卖者要价会导致价格下调。有以下特殊的竞价方式值得注意:
- 拍卖. 买方竞价知道需求量等于供给量。用于供给量固定的产品。
- 集合竞价. 将所有申报的买入和卖出信息综合成供给和需求曲线,求其交点(成交价),所有能发生的交易都以成交价成交。多用于决定股票的开盘价。
- 连续竞价. 按照价格优先和时间有限的原则,对买卖申报逐笔连续撮合。多用于股票开盘后的竞价。
- 一口价. 卖方直接要价,take-or-leave-it。
而完全竞争下的长期均衡的条件又有不同。如果有企业营利,就会有新的竞争者加入;如果企业亏损,它就会退出市场。因此,长期均衡的条件是价格 = 边际成本 = 平均成本 = 收入之和。
竞争和垄断
首先考虑什么叫“竞争”。在传统经济学中,完全竞争是如下的理想模型:
- 行业没有明显的进入壁垒和退出壁垒;
- 大量小规模生产厂家;
- 所有厂家生产完全一样的标准化产品,质量和性能没有任何差别;
- 存在着完全的信息,没有不确定性;
- 生产者都是价格接受者,所有厂商按相同的价格出售产品。
那么,单个厂商的均衡都是在价格等于边际成本之处,整个市场的均衡在市场供给等于市场需求处。
可以用市场集中度来刻画垄断的程度。两个代表性的指数是:
- $n$-企业集中度. 市场份额前 $n$ 的企业占据的总市场份额。
- Herfindahl-Hirschman Index.
而如果形成了独家垄断,一个重大区别就是企业将获得完全的定价权。此时,垄断企业将求解如下的优化问题来决定定价:
$$
\max \Pi = yp(y) - C(y)
$$
其最优解位置在边际收益等于边际成本之处,有
$$
p(y) + y\frac{\mathrm{d}p}{\mathrm{d}y} = MC \label{optimal_price}
$$
定性地看这个函数,因为需求原则 $\mathrm{d}p / \mathrm{d}y < 0$,因此最优垄断价格大于边际成本,并且随边际成本上升而上升。此时,因为产量减少,导致生产者剩余和消费者剩余之和减少,减少的部分称为社会净损失($AEE^*$)。
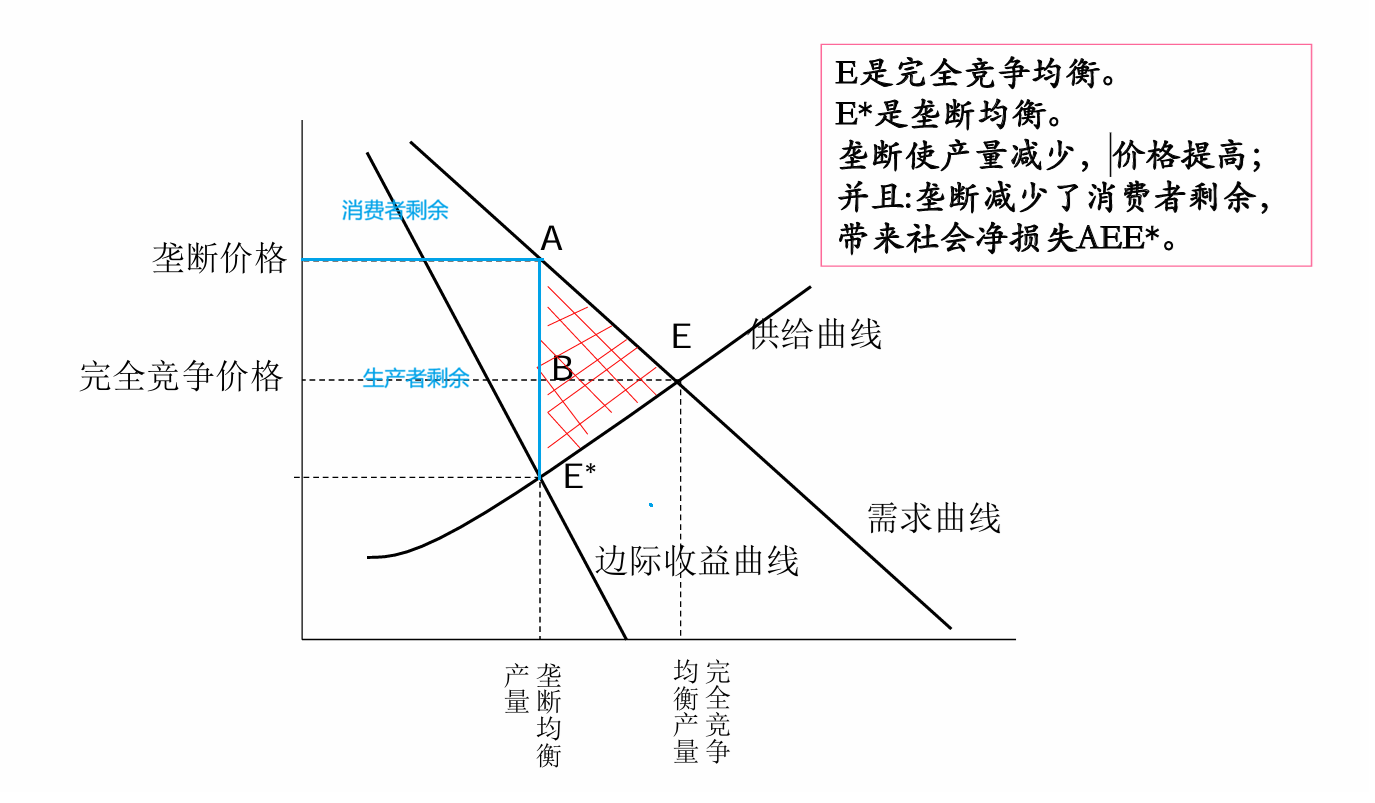
现在我们考虑垄断企业如何进行定价。最优的条件由 $(\ref{optimal_price})$ 给出,此时定义勒纳垄断势力指数
$$
L = \frac{p - MC}{p} = -\frac{\mathrm{d}p}{\mathrm{d}y}\frac{y}{p} = \frac{1}{\varepsilon}
$$
其中 $\varepsilon$ 为需求弹性的绝对值。此时可将价格定为 $p = \frac{MC}{1 - 1 / \varepsilon}$。
另一类定价方法是价格歧视,分为
- 一级价格歧视. 对不同消费者收取不同的价格,且都等于消费者的保留价格。此时,厂商可以获得全部的消费者剩余,但是产量是社会最优的。
- 二级价格歧视. 根据购买量不同收取不同的单位计费(电信业的分段计费);
- 三级价格歧视. 对不同需求曲线的市场收取不同的价格(如学生票)。
价格歧视的问题是没有充分的信息导致难以开展,另外消费者之间可能发生套利。搭售则是一种替代方案。即将不同产品捆绑做一个套餐销售,消费者对不同产品有不同的评价,但是都愿意购买这个套餐。
现在考虑垄断程度比较高但是不极端,即寡头竞争的情形。我们只讨论两个企业之间的短期竞争手段(价格、产量等)。对于中长期的产品选择、研究开发等手段,因为没法算,这里不讨论。
Cournot 模型(产量竞争). 各企业同时选择自己的产量,价格由市场供需关系决定。
此时,两个企业的利润函数为
$$
\Pi_i(q_1, q_2) = q_iP(q_1 + q_2) - C_i(q_i)
$$
这里就有一个由如下方程组给出的纳什均衡:
$$
\begin{cases}
\frac{\partial \Pi_1(q_1, q_2)}{q_1} = 0 \\
\frac{\partial \Pi_2(q_1, q_2)}{q_2} = 0
\end{cases}
$$
其中第一个方程给出 $q_1^*$ 和 $q_2$ 的关系 $q_1^* = R_1(q_2)$,第二个方程给出 $q_2^* = R_2(q_1)$,称为两个企业各自的反应函数。
一个特例是需求为线性函数,成本为相同的线性函数,则纳什均衡的结果就是两边生产相同数量的商品。
Bertrant 模型(价格竞争). 两个企业以同样的成本生产完全相同的产品,价格低的一方获得全部的市场份额,价格相同则评分市场。
此时的均衡价格就是边际成本。