Revision | 计算机组成与体系结构（上）

Posted on 2025-11-02 Edited on 2025-11-06 In Revision Notes

历史
计算机的基本结构
CISC 与 x86 指令系统
- x86 寄存器和访存模型
- x86 指令选讲
RISC 与代表指令系统
- MIPS
- RISC-V 和 ARM
运算器
- 基础
- 加法器
- 乘法器
- 除法器
单周期中央处理器
控制器

历史

世界上第一台通用电子计算机是 ENIAC（Electronic Numerical Integrator And Computer，电子数字积分器和计算机）。该计算机于 1946 年 2 月 14 日建成于美国宾夕法尼亚大学，主要设计者是 John Mauchly 和 John Presper Eckert Jr.，现存于美国硅谷计算机博物馆。其性能参数如下：

性能	电子管数	功率	占地面积	重量	成本
5000 次加法 / 秒	18000	150 千瓦	170 平方米	30 吨	40 万美元

事实上，被认为是世界上第一台电子计算机的是 ABC（Atanasoff-Berry Computer），该计算机设计于 1937 年，并在 1942 年成功测试。电子管、二进制、逻辑单元、存储器等技术均在该计算机中应用。但该计算机并不通用，不可编程，仅能用于求解线性方程组。

1945 年 6 月 30 日，“计算机之父”，美籍匈牙利数学家冯·诺伊曼向美国陆军机械部提出《关于 EDVAC 的报告草案》。该草案指出

ENIAC 的开关定位和转插线只不过代表着一些数字信息，完全可以像受程序管理的数据一样存放于主存储器中。

这便是“存储程序”，也即冯诺依曼结构之核心思想的渊源。该报告催生的计算机 EDVAC（Electronic Discrete Variable Automatic Computer，离散变量电子计算机）于 1949 年 8 月交付，但直至 1951 年才正式运行，并于 1962 年退役。其主要特点为

实现了存储程序概念，提升了任务效率；
使用二进制存储数据，简化了逻辑线路；
由五个基本部分构成：运算器、控制器、存储器、输入设备、输出设备。

由于 EDVAC 的延迟正式运行，世界上第一台冯诺伊曼结构的电子计算机之桂冠为英国剑桥大学数学实验室的莫里斯·威尔克斯主导设计的 EDSAC（Electronic Delay Storage Automatic Calculator，电子延迟存储自动计算器）所截胡。冯诺伊曼结构的五个基本成分，在 EDSAC 中的实现情况依次为：运算器、控制器（电子管），存储器（水银延迟线），输入设备（打孔纸带），输出设备（电传打印机）。

电子计算机的商用之帷幕，为由埃克特-莫克利（即 ENIAC 的设计者）计算机公司（EMCC）设计、雷明顿·兰德公司建造建造的 UNIVAC（Universal Automatic Computer）所拉开。该型计算机主要面向商业和行政管理类用户、强调快速数据传输和大量简单运算的能力、设计时即考虑量产的要求。最后，总计售出 46 套，并于 1952 年准确预报了美国总统选举结果，一夜成名。

此后的 1950 年代中，众多公司进入电子计算机领域。值得一提的是，IBM 公司于 1953 年成功转型，并在 1955 年占据了 70% 的市场份额。

计算机按照尺寸主要分为四类：超级计算机 / 巨型机、大型计算机 / 主机、小型计算机 / 中型机、微型计算机 / 微机。

大型计算机

使用所在时代的先进技术构成的一类高性能、大容量通用计算机。
强调告诉输入输出、海量存储空间和并行事务处理等方面的特性。
以面向大容量数据的事务处理为主，兼顾科学计算。

代表机器：

IBM S/360（1964）。其每秒可只需 34000 条指令。
IBM zEC12（当代）。6 核处理器，主频 5.5GHz，高速缓存 2MB L2 / 48MB L3 / 384MB L4，3040GB 内存。

超级计算机.

运算速度最快、性能最高、技术最复杂的一类计算机；
代表该时期处理能力（尤其是运算速度）巅峰；
解决科技领域中某些巨大的挑战性问题的关键工具。
适用于高度计算密集型的科学计算任务。

代表机器：

CDC600（西摩·克雷，1964）

计算机的基本结构

此处考虑冯·诺伊曼结构的计算机。在这种结构中，计算机应当由五大部分组成：运算器（CA）、控制器（CC）、存储器（M）、输入设备（I）、输出设备（O）。除开这个组成，该结构的要点是

数据和程序以二进制形式不加区别地存放在存储器中，位置由地址指定；
计算机工作时能够自动地从存储器中取出指令加以执行。

现实中的计算机将这些组成部分放置在主板上。早期的主板布局包含：

CPU
北桥芯片. 其中包含 PCIe 控制器、集成显卡、主存控制器。主存控制器连接主存；PCIe 控制器可连接 PCIe 显卡，进而连接显示器。
南桥芯片. 主管 I/O，连接硬盘、网络、音箱、键盘、USB 设备、PCI 卡等。

后来，主存控制器首先被集成到 CPU 中。接下来，北桥芯片消失，其中的 PCIe 控制器被集成到 CPU 中；集成显卡被分成图形模块和显示模块；前者被合并进 CPU后者被合并进原南桥（合并后称为 Platform Controller Hub）

将整个计算机集成为单一芯片的集成电路称为系统芯片（System-on-a-Chip，Soc），在智能手机和平板电脑上应用广泛。得益于技术进步，集成电路能够越做越小。关于这个现象，一个知名的表述是摩尔定律：价格不变时，集成电路上可容纳的晶体管数目倍增，性能随之倍增。

值得一提的是，随着计算机图形学的发展，一类专用于图形处理的芯片，GPU，应运而生。这类芯片几乎处处为高吞吐量而非低延迟服务以适应图形处理任务中大量的数学运算。其和 CPU 的对比由下表直观展示：

	CPU	GPU
ALU	少量，低延迟	大量，节能，高延迟，但高度流水线化
控制	复杂。含有分支预测、数据转发等	简单。无分支预测、数据转发
Cache	大	小

可见在 GPU 上必须仔细设计高度并行的算法，方可转代价为优势。

最后简述一下计算机上执行指令的过程。执行一条指令分为四个阶段：取指（F）、译码（D）、执行（E）、写回（W）。各阶段中计算机的行为如下：

取指. 控制器将指令地址送至存储器，存储器按照地址读取内容送回控制器。下面是详细的流程，注意 2，3，行本质上是一次访存操作的模板，此后不再赘述。
- PC 寄存器的值经内部总线发送至 CPU 中的 MAR 寄存器；
- MAR 寄存器中的值经地址总线发送至存储器中的 MAR 寄存器，同时控制电路通过控制总线发送 Read 信号至存储器的控制逻辑；
- 存储器的地址译码器读取 MAR，计算出对应位置存储的值，放在 MDR 处；
- 存储器的控制逻辑经控制总线发送信号 Ready 给 CPU，同时 MDR 通过数据总线发送至 CPU 的 MDR 寄存器；
- CPU 中的 MDR 寄存器的值经内部总线发送至 IR 寄存器，取指结束。
译码. IR 寄存器中的指令发送至 CPU 的指令译码器，然后控制电路发送相关信号。
执行. 控制器从寄存器或存储器中取出操作数（回忆取出操作数之后结果存在 MDR 中），将相应寄存器的值经内部总线发送至 ALU 的输入。
写回. 将 ALU 的输出经内部总线送至对应的寄存器（如果要写回内存，则送至 MDR）。

CISC 与 x86 指令系统

CISC（Complex Instruction Set Computer）乃是两大主流体系结构之一。而 x86 又是 CISC 中最有代表性的一种指令系统。每一款 x86 处理器都包含该系列早期处理器的全部指令、寄存器和操作方式（兼容性），仅进行已有指令的功能改进和新增新指令。x86 发展历程中的代表 CPU 及其参数如下表所示：

型号	位数	地址位数	年代	备注
Intel 8086	16	20	1978	物理地址采用段 + 偏移
Intel 8088	16	8	1981	8086 的简化版
Intel 80286	16	24	1982	以“实模式 / 保护模式”兼容 8086 的工作方式
Intel 80386	32	32	1985	增加“V8086”模式，可模拟多个 8086 处理器
AMD Opteron	64	64	2003

实模式. 80286 以上的处理器采用 8086 的工作模式，即为实模式。
保护模式. 80386 及以上处理器的主要工作模式，引入了：多任务、设置特权级、特权指令执行、访问权限检查、4GB 访存、虚拟存储器。

处理器通电 / 复位之后首先进入实模式，然后操作系统将运行在保护模式下。V8086 模式为保护模式下的一种特殊工作状态，与实模式类似，不同之处在于中断处理。

x86 寄存器和访存模型

这里以 8086 为例介绍 x86 结构的寄存器模型。其寄存器可以分类整理作

通用寄存器. 可以存储一切数据，但是各有特殊用途。进一步细分为：
- 数据寄存器. 每个都可以分为 *H 和 *L 两个 8 位寄存器使用。
  - AX （Accumulator）存放乘除的操作数；
  - BX （Base）存放存储单元的偏移地址；
  - CX （Count）存放计数值；
  - DX （Data）乘法运算产生的部分积和除法运算的部分被除数。
- 指针和变址寄存器. 均为 16 为，SP 和 BP 用于堆栈操作，DI 和 SI 用于串操作。
  - SP （Stack Pointer）堆栈指针寄存器；
  - BP （Base Pointer）堆栈基址寄存器；
  - SI （Source Index）源变址寄存器；
  - DI （Destination Index）目的变址寄存器。
指令指针寄存器. IP。
标志寄存器. FLAGS。其中包含若干标志位，可分为状态标志和控制标志。
- 状态标志. 反应 CPU 的工作状态。
  - CF （进位标志）第 0 位；
  - PF （奇偶标志）第 2 位；
  - AF （半进位标志）第 4 位；
  - ZF （零标志）第 6 位；
  - SF （符号标志）第 7 位
  - OF （溢出标志）第 11 位；
- 控制标志. 对 CPU 的运行起特定控制作用。
  - TF （跟踪标志）第 8 位；
  - IF （中断标志）第 9 位；
  - DF （方向标志）第 10 位。
段寄存器. CS，DS，ES，SS。这几个寄存器的用途在后面的访存模型中说明。

至于 32 位和 64 位，无非是将通用寄存器、指针和变址寄存器、标志寄存器拓宽（同时增加了一些标志），并增加一些段寄存器。IA32 增加了两个段寄存器 FS 和 GS。

x86 的访存采用经典的“段：偏移”方式。逻辑地址由两部分构成：[Base:Offset] 段基址、偏移量，经过地址加法器计算得到物理地址。

对于 8086，其段基址存在于段寄存器之中。各寄存器的含义为：CS（代码段寄存器），DS（数据段寄存器）、ES（附加段寄存器）、SS（堆栈段寄存器）。地址加法器通过段基址乘以 16 加偏移量来计算物理地址。

进入 IA32 的保护模式，寻址仍然采用段：偏移模式。然而需要察觉如下要素：

寻址允许段基址是任何 32 位整数；
段寄存器只有 16 位。
偏移量为 32 位；
段偏移不应当超过段长度，这里段长度也不是 $2^32$。

看似两两矛盾。解决方案是段基址不被存在段寄存器中，而是被存在存储器中。实践中，CPU 首先拿着全局描述符表寄存器 GDTR 找到全局描述符表 GDT 的起始地址，然后以段寄存器乘以 8 作为偏移（可以认为，GDT 是一个每项 64 位的数组），找到对应的表项，然后从表项中找到段基址和段界限（Segment Limit，即段长），再交给地址加法器得到物理地址。

GDT 表项的 8 个字节从低到高依次是：段界限（2 字节），基地址低位（3）字节，权限（1 字节），其他（1 字节），基地址高位（1）字节。

x86 指令选讲

众所周知，汇编语言乃是机器码的助记词写成的较低级编程语言。在讲解 x86 指令时，我们必不可能直接对着机器码说明，而是对着汇编语言说明。

x86 的汇编语言主流格式分为 Intel 格式和 AT&T 格式。前者为 Intel 所制定，主要应用在 MS-DOS 和 Windows 系统中；后者由 AT&T 制定，源自贝尔实验室研发的 UNIX，最初哟弄个在 PDP-11 / VAX 等机型，后来迁移到 x86，现在主要用在 UNIX / Linux 系统中。两者的主要区别罗列如下：

	Intel	AT&T
操作数前后缀	没有前缀，后缀（H / O）指示立即数进制	立即数前缀 `$`，寄存器前缀 `%`，`0x` 指示十六进制
操作数方向	先目的后源	先源后目的
内存偏移量	用 `[base + index * scale + disp]` 标识	用 `disp(base, index, scale)` 标识
操作码后缀	操作码无后缀，用内存单元操作数前缀指明操作数大小如 `mov eax, dword ptr [ebx]`	操作码后缀指明大小如 `movl (%ebx), %eax`

早期的汇编语言按分段结构进行组织。每段格式为

1
2
3

(NAME) SEGMENT 
        ...   ; 代码
(NAME) END

对应 x86-64 汇编中的

1 2	section .(name) ... ; 代码

本文汇编均用 Intel 格式。由于指令编码确实太阴间了，这里就不考虑了。

传送指令. MOV dst, src，将 src 中的数据传送到 dst 中。

注意传送方向有以下限制：

立即数不能作为 dst；
dst 和 src 不能同是存储单元；
立即数不能传到段寄存器；
CS 不能作为目的寄存器；
段寄存器之间不能相互传送。

交换指令. XCHG opr1, opr2，交换两个操作数。

不允许交换两个存储器；
不允许使用段寄存器。

加法指令. ADD dst, src / ADC dst, src / INC dst，表示加法 / 带进位加法（dst += src + cf） / 加 1。

仅有以下三种：

存储器 / 寄存器加给寄存器；
立即数加给存储器 / 寄存器；
立即数加给 ax。

注意这里看似第三类被第二类包含，实则不然。第三类的指令长度显著短，这是出于缩短平均程序长度之考虑。

关于逻辑运算、栈操作指令，我们在 ICS 中已经学过，这里不再谈论。

查表指令. XLAT。假设数据段存在一个每项一字节的表。本指令从 BX 中取得表起始地址，AX 中取得下标，查到结果后存入 AL。

加法十进制调整指令. DAA。将 AL 转成 BCD 码。

无条件转移. JMP LABEL。分为直接转移和间接转移。直接转移包括

短转移. JMP SHORT LABEL $\mathrm{IP}\leftarrow \mathrm{IP} + \text{Offset ($8$ bit)}$；
近转移. JMP NEAR PTR LABEL $\mathrm{IP}\leftarrow \mathrm{IP} + \text{Offset ($8$ bit)}$；
远转移. JMP FAR PTR LABEL 查询 Label 所在的段基址 CS 和偏移量 Offset，$\mathrm{IP}\leftarrow \mathrm{CS:Offset}$

可以想象，自上而下这几个指令的长度为 2 byte，3 byte，5 byte。

间接转移形如 JMP DWORD PTR opr。作用为寻址到 opr 指定的存储器单元所在的双字，将低位传送到 IP，将高位传送到 CS。

条件转移指令. JXX LABEL。诸条件跳转的含义和对应的判断条件在 ICS 里已经学过了。这里只需记住无符号数是 JA / JB，有符号数是 JL / JG。

循环控制指令. LOOPXX LABEL。令 CX 减 1 并改变条件码。当 XX 指出的条件成立时跳转到 LABEL。

处理器控制指令. 包括一系列改变条件码的指令，以及 HLT（暂停），WAIT（等待），ESC（交权），指令前缀 LOCK（封锁总线），NOP（空操作）等。

串操作指令 是一类复杂的 x86 指令。总体上，包含以下的指令：

串操作指令. 助记词后面加 B / W，表示串元素是字节还是字。
- MOVS 串传送；
- CMPS 串比较；
- SCAS 串扫描；
- LODS 取串；
- STOS 存串；
重复前缀.
- REP 无条件重复；
- REPE / REPZ 相等 / 为零时重复；
- REPNE / REPNZ 不相等 / 不为零时重复。

串操作指令隐含了源的地址为 DS:SI，目的地址为 ES:DI，串长存在 CX 中。运行一次串操作指令，处理器除了会完成字面上的操作之外，还会更新 SI 和 DI 并将 CX 减 1。此处，SI 和 DI 更新的方向（加或是减）由方向标志 DF 指定。若 DF 为 0，其将增加；若 DS 为 1，其将减少。回忆 DF 可以用处理器控制指令设置，具体地，STD 置 DF 为 1，CLD 置 DF 为 0。

此处之所以指定方向，是为了处理源串和目的串地址交叠的情况。

RISC 与代表指令系统

RISC 与 CISC 之争是体系结构领域老生常谈的问题。CISC 的兼容性和设计思路决定了其复杂程度必然高，RISC 则反其道而行之。本节将简述三类 RISC 指令系统。

MIPS

无流水线互锁微处理器（Microprocessor without Interlocked Pipe Stages）是 RISC 已经不再流行的开创性工作。历史上，两个 32 位的版本，MIPS I 和 MIPS II 分别于 1985 年被应用于 R2000 CPU、于 1990 年被应用于 R3000 CPU。1992 年的 R4000 上的 MIPS III、1994 年 R8000 上的 MIPS IV 和 1996 年的 MIPS V 为拓展至 64 位的版本。1999 年的、分别以 MIPS II 和 MIPS V 为基础，融合诸版本特性的 MIPS32 和 MIPS64 是最后的现代化版本。此后，MIPS 逐渐推出历史舞台。

MIPS 主要关注减少指令类型和降低指令复杂度。其主要特点为：

指令等长。 这将简化取指。
只要 Load 和 Store 能访存。
寻址模式简单。 仅支持 ($r) 和 d($r)。
指令数量少，功能简单。 这将简化指令的执行过程。

由此可见，本指令系统对应的 CPU 设计简单且快速，但是编程复杂、程序更长且需要优秀的编译器。

MIPS 的寄存器模型为 32 个 32 位宽的通用寄存器（此表和网络上的某个版本不一致，我们仅能以课程为准）：

编号	名称	用途
0	`$zero`	常量 $0$
1	`$at`	（Assembler Temporary）汇编暂存，保留给汇编器使用
2-3	`$v0`，`$v1`	存储子程序返回值
4-7	`$a0` - `$a3`	调用函数的前 4 个参数
8-15	`$t0` - `$t7`	临时变量
16-23$^*$	`$s0` - `s7`	临时变量
24-25	`$t8` - `$t9`	临时变量
26-27	`$k0` - `$k1`	为内核预留
28$^*$	`$gp`	全局指针
29$^*$	`$sp`	栈指针
30$^*$	`$fp`	帧指针
31$^*$	`$ra`	返回地址

其中标注 $^*$ 的表示调用者保存寄存器。对应的指令非常简单，完整的手册仅一页纸：

指令的分类、作用在表中一目了然，这里不再重复。

RISC-V 和 ARM

摆了。

运算器

基础

现代集成电路通常使用 MOS（金属-氧化物-半导体）晶体管。MOS 管共有两种，分别为 NMOS 和 PMOS。这个原件有三个针脚，称为门极（Gate），源极（Source）和漏极（Drain）。NMOS 在 Gate 为高电位时，Source 和 Drain 导通；PMOS 在 Gate 为低电位时，Source 和 Drain 导通。由 NMOS 和 PMOS 构成的集成电路称为互补 MOS（CMOS）集成电路。两种晶体管的符号想必大家非常熟悉，PMOS 比 NMOS 多了一个圈，这里不写。

众所周知 $\{\mathrm{NOT}, \mathrm{NAND}, \mathrm{NOR}\}$ 是一个完备的门集合。这几个门可以直接用 CMOS 实现：

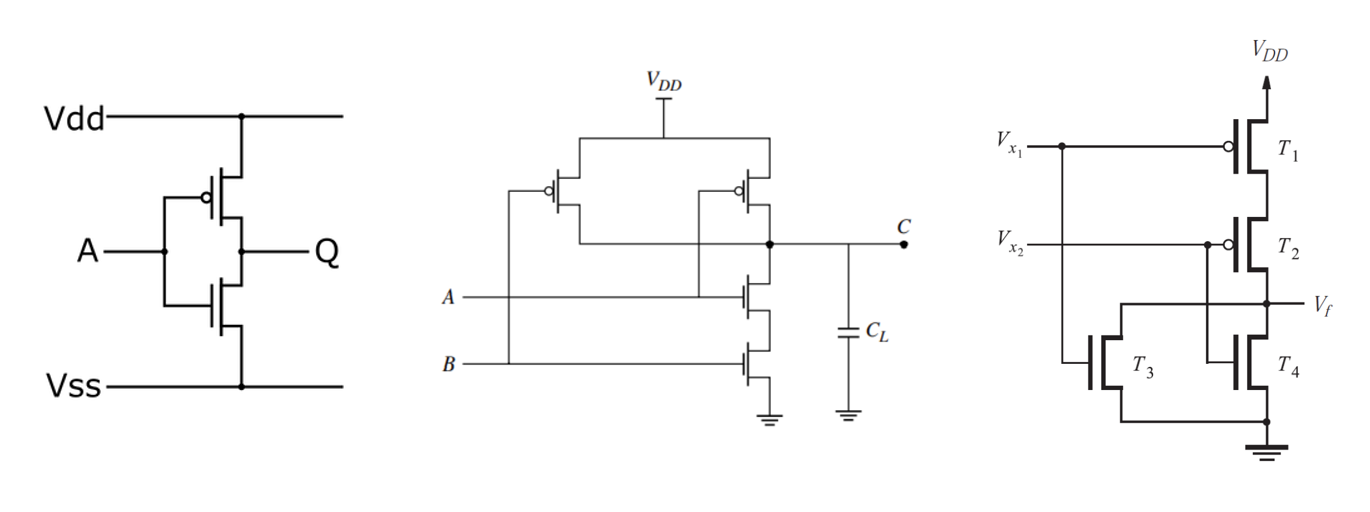
可以发现，如果将 $\mathrm{NAND}$ 的 PMOS 和 NMOS 互换，则可以得到 $\mathrm{AND}$。然而之所以不这么做，是因为 NMOS 不能接电源、PMOS 不能接地，否则会发生电压衰减。至此，逻辑运算可以通过并联位数多个逻辑门来实现。ALU 乃是一个多功能的元件，其内部包含多种并联的运算和一个多路复用器：首先计算所有种运算的结果，然后用多路复用器选出特定运算的结果。

为了实现寄存器等工具，需要使用 RS Latch 构造 D Latch，进而构造 D flip-flop。D flip-flop 这个元件的功能是在始终上升沿将输入传播到输出并锁存。关于其构造，我们在 ICS 课程中已经见过，因此这里不写。

可以想象，并联 D flip-flop 将得到通用寄存器；串联 D flip-flop 将得到移位寄存器：在始终上升沿寄存器内存储的数据右移一位。想要实现任意多位的移位寄存器，可以考虑两条朴素的路线：

等待 $x$ 周期，将输出 a >> x；
做 $32$ 个移位寄存器来移动 $0, 1, …, 31$ 位，用多路复用器选择结果。注意多路复用器可能很慢。

一个平衡周期数和延迟的方法是使用 $\log n$ 层二路复用器网络。第 $i$ 层决定要不要右移 $2^{i - 1}$ 位。这样一来，你确实可以用低延迟 $1$ 周期完成任意的移位。

加法器

实现加法器从半加器开始。半加器这个元素在输入 $A, B$ 上计算 $(A\oplus B, A\wedge B)$。容易发现，前后两分量分别是加法的本位结果和进位。为了构造完整的加法器，需要把进位也考虑在内。一个全加器 $\mathscr{A}(A, B, C_{in})$ 将计算

$$
(S, C_{out}) = (A\oplus B \oplus C, (A \wedge B) \vee ((A\oplus B)\wedge C))
$$

那么容易想到下面的这些 $n$ 位全加器构造：

行波进位加法器 首先考虑有 $n$ 个 1 位全加器 $\mathscr{A}^1, …, \mathscr{A}^n$。直接将 $C_{out}^i$ 和 $C_{in}^{i + 1}$ 连接，便得到一个 $n$ 位全加器。这个构造称为行波进位加法器（RCA）。

RCA 的缺陷在于其关键路径（延迟最长，i.e 经过门数量最多的路径）为

$$
A^1\rightarrow C_{out}^1\rightarrow C_{in}^2 \rightarrow C_{out}^2 \rightarrow \cdots \rightarrow C_{out}^n
$$

这条路径的长度为 $3 + 2(n - 1) = (2n + 1)$。我们说 RCA 的总延迟为 $(2n + 1)T$，其中 $T$ 为门延迟。在 28mn 制程下，这个值是 0.02ns。众所周知 CPU 的主频取决于各阶段的延迟之最大值，为了设计高频率的 CPU，务必要优化这个延迟。

一个直接的想法就是优化进位的计算。注意进位

$$
C_i = (A_i \wedge B_i) \vee ((A_i \oplus B_i) \wedge C_{i - 1})
$$

定义生成信号 $G_i = A_i \wedge B_i$，传播信号 $P_i = A_i \oplus B_i$，有（这里简明起见，把 $\vee$ 写作 $+$，把 $\wedge$ 写作 $\cdot$）

$$
C_i = G_i + P_i \cdot C_i
$$

将 $C_i$ 的逻辑表达式暴力算出后，可以展开成关于 $G_i, P_i$ 的析取范式。注意 $n$-bit $\mathrm{AND}$ 和 $n$-bit $\mathrm{OR}$ 都被视为 $1T$ 的门，因此只需要 $3T$ 便可计算 $C_i$。

超前进位加法器. 首先利用上述办法算出 $C_i$，然后用全加器算出 $C$。这种加法器称作 CLA。

注意到无论 $n$ 几何，超前进位加法器的延迟都是 $4T$。然而，进位计算器的宽度是指数爆炸的，且 $n$-bit 逻辑门很难做。因此实践中的折衷办法是串联几个 CLA，称作 $k$ 级 CLA。容易算出 $k$ 级 CLA 的延迟为 $2(k + 1)T$。因此，如果用 4 级 CLA 实现 32 位加法器，则延迟为 $10T$，而如果单纯用 RCA，延迟为 $65T$，提升显著。

乘法器

乘法的计算无非是列竖式。因此容易想到这种最简单的乘法器构造：

$N$ 位乘法器. 考虑两个移位寄存器，称作乘数寄存器和被乘数寄存器，和一个普通寄存器，称为乘积寄存器，位数依次为 $N, 2N, 2N$。给定一个 $N$ 位的加法器。可通过这样一个控制逻辑来计算乘法：

If 乘数寄存器最低位为 $1$：
$\qquad$ 令乘积寄存器变为乘数寄存器加被乘数寄存器；
令乘数寄存器右移一位；
令被乘数寄存器左移一位。
If 已经是第 $n$ 轮循环：结束。否则继续循环。

其中 If 判断无非是一些组合逻辑，但是加法、左移、右移都需要一个周期。因此我们得到了一个 $3N$ 周期的 $N$ 位乘法器。最直接的优化便是将加法和移位并行，若乘数寄存器最低位是 $0$，令乘积寄存器锁存，周期结束时令乘数寄存器和被乘数寄存器移位。新的乘法器为 $N$ 周期。

更给力的优化是考虑计算资源。注意到被乘数寄存器（$M$）和乘积寄存器（$A$）的有效位数互补，且加法总是只需要 $n$ 位加法（低位不影响），可以将 $Q\Vert A$ 拼在一起放在一个 $2N$ 位寄存器中，控制逻辑变成：

将乘积寄存器初始化为乘数；
If 乘积寄存器最低位为 $1$；
$\qquad$ 令乘积寄存器的高 $N$ 位加上乘数寄存器；
令乘积寄存器右移一位。

现在只需要一个 $2N$ 位的移位寄存器、一个 $N$ 位的普通寄存器和一个 $N$ 位加法器，并且仍然可以用此前的手法并行化加法和位移，总周期数为 $N$，但是硬件资源显著减少。

最后，如果你能看被乘数的后两位，就可以想到这样的一个构造：若最后两位是 $10$，让乘积寄存器减去乘数寄存器；若最后两位是 $01$，让乘积寄存器加上乘数寄存器。本质上这就是 $1^n = 10^n - 1$。这样的构造称为 Booth 乘法器，可以减少加法次数。

除法器

除法器所作工作是模拟所谓的“厂除法”。假设你有一个 $2N$ 位的除数寄存器，一个 $2N$ 位的余数寄存器，一个 $N$ 位的商和一个 $2N$ 位的加减法 ALU。容易写出如下的控制逻辑：

令余数 $\leftarrow$ 余数 $-$ 除数；
If 余数 $ \geq 0$：
$\qquad$ 商左移一位或上 $1$；
Else：
$\qquad$ 回滚操作；
$\qquad$ 商左移一位；
除数右移一位。
If 已是第 $33$ 轮：退出；否则继续循环。

观察到余数寄存器有效位数和商的有效位数互补，且仅需要对余数有效位数最高的 $N$ 位做加减。此时惯用的手法是将其拼接，然后除数寄存器便无需 $64$ 位，并且无需支持移位；ALU 只需要 32 位。

回忆乘法中也有一个拼接的寄存器。实践中，这两个拼接寄存器是同一个位置。因此，这个寄存器需要同时支持左右移动。

注意，这里你必须要先知道余数 $-$ 除数的结果，才能知道要不要回滚操作。因此，无法像乘法一样并行。

单周期中央处理器

现在，想要设计一个完整的单周期处理器。应当遵从的步骤为：

分析指令系统，得出对数据通路的需求；
为数据通路选择合适的组件；
连接组件建立数据通路；
分析每条指令的实现，以确定控制信号；
集成控制信号，形成完整的控制逻辑。

为了搭建一个示例的 CPU，我们仅考虑 MIPS 指令集的下面几个指令：

无符号数加减. addu，subu；
立即数逻辑或. ori；
访存指令. lw，sw；
条件分支. beq。

那么，显然除了 32 位的存储器和 IR 之外，还可以根据指令的操作内容梳理出以下这些需求：

指令	操作	需求
`addu / subu rd, rs, rt`	`R[rd] <- R[rs] + R[rt], PC <- PC + 4`	32 位可修改、同时访问两个位置的寄存器；ALU
`ori rd, rs, imm16`	`R[rd] <- R[rs] \| zeroExt(imm16), PC <- PC + 4`	零扩展器，ALU，运算操作数可以是扩展后的立即数
`lw / sw rt, imm16(rs)`	`R[rt] <- MEM[R[rs] + signExt(imm16)]; PC <- PC + 4`	符号扩展器
`beq rs, rt, imm16(rs)`	`PC <- PC + (rs == rt)? signExt(imm16)\|00 : 4`	比较两个数，两种修改 PC 的模式

总的来说，我们将需要这些组件：

ALU. 支持加减或；
立即数扩展组件. 支持零扩展和符号扩展；
PC 寄存器. 支持两种加法，加 $0$ 或者加立即数；
寄存器堆. 支持读 rs 和 rt，写 rs 或 rt。因此，需要两个读口一个写口（寄存器编号），一个写使能信号，一个数据接口 busW，两个出口 busA，busB。
存储器. 一个只读指令存储器，一个可读写数据存储器，均为 $32$ 位；因此，需要地址接口，一个写使能信号，一个数据接口 DataIn 和一个输出 DataOut。

根据指令，可以知道我们所需要的连线无非是这样：

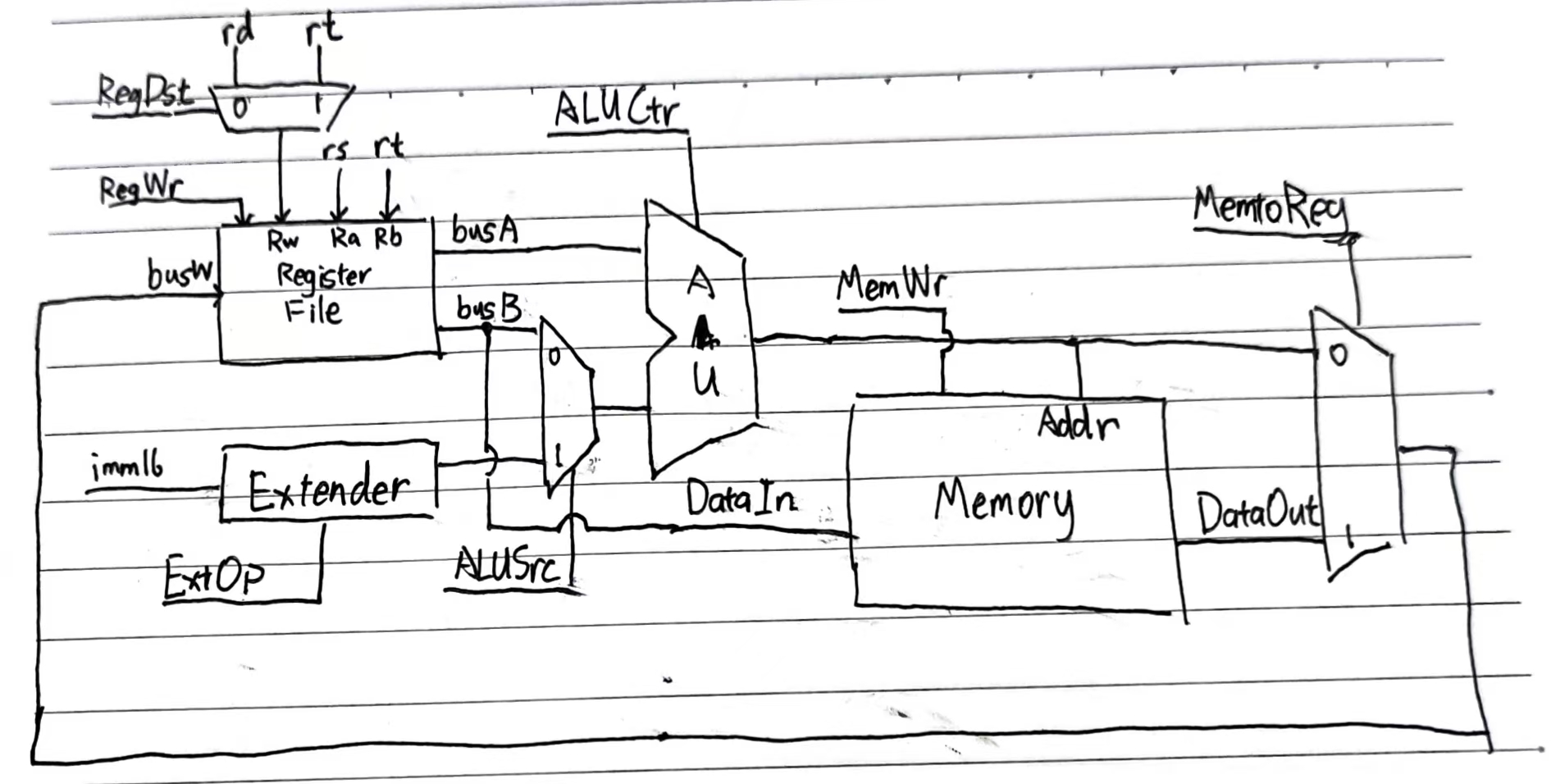
当然，你还需要一个称为 IFU（Instruction Fetch Unit）的东西来根据指令的 opcode 生成图中的这些信号。这个就是一些组合逻辑，这里不谈。

控制器

在上一节中，可以看到控制器和 ALU 非常耦合。我们现在让控制器更加独立一点，我们期望获得一个结构，能够根据指令顺次发送一系列命令。命令的执行交由下层硬件（包括总线）完成。

现在想象指令 LOAD R1, M1 被从存储空间中取出并执行的过程。它可以被拆解成：

控制器发指令 $\mathrm{PC}_{out}$ 和 $\mathrm{MAR}_{in}$ 信号。 内部总线将 PC 传送到 MAR；
控制器发指令 $\mathrm{M}_{read}$ 信号。 数据总线将 $M[MAR]$ 传送到 MDR；
控制器发指令 $\mathrm{PC}_{add}$ 信号。 某个运算单元使 $PC \leftarrow PC + n$，其中 $n$ 为指令长度；
控制器发指令 $\mathrm{MDR}_{out}$ 和 $\mathrm{IR}_{in}$ 信号。 内部总线将 MDR 送到 IR；

至此取指完成。然后控制器发现指令是这条 LOAD R1, M1，于是：

控制器发指令 $\mathrm{IR}_{out}$ 和 $\mathrm{MAR}_{in}$。 内部总线将要读的地址送到 MAR；
控制器发指令 $\mathrm{M}_{read}$ 信号。 数据总线将 $M[MAR]$ 传送到 $MDR$；
控制器发指令 $\mathrm{MDR}_{out}$ 和 $\mathrm{R1}_{in}$。 内部总线将 MDR 传到 R1。

这些指令，又称为微命令。顾名思义，即比指令还要小的机器层面的原子操作。

指令执行完成。其余指令的执行，大同小异，这里不再赘述。

注意到，为了实现这样的一个结构，有两种显然的选择：

把控制器的写死在电路板上。这种控制器称作硬布线控制器；
在一个叫做 MicroROM 的结构上存储控制器的软件代码，然后控制器相当于一个小 CPU 来执行这些代码。这种控制器称为微程序控制器。

硬布线控制器. 主要包含以下结构：

环形脉冲发生器. 循环地产生信号 $T1, T2, T3, …$，接收到 End 信号就复位。
指令译码器. 确定 IR 里面是哪条指令；
微命令编码器. 一个组合逻辑，根据环形脉冲发生器生成的脉冲信号和指令译码器的结果同步产生相应的控制信号。

之所以容易这样做，是因为你注意到比如 Load 指令执行过程中要顺次发出 $8$ 组信号（上面 $7$ 条加一个 End），则

$$
\mathrm{MAR}_{in} = (\mathrm{Load} \wedge (T1 \vee T5)) \bigwedge \text{Similar DNF from another instruction}
$$

控制信号可以方便地写成逻辑表达式，从而写成电路。

此类控制器的优缺点相当明显：

优点. 指令执行速度快；
缺点. 电路复杂，设计和验证难度大，难以扩充和修改。

微程序控制器. 主要包含以下组件：

控制存储器（CM）. 一个 ROM，里面存放微程序。其中每个条目为以下格式：（微操作控制字段：顺序控制字段）。前者将给出对应需要发送的信号（既可以直接存，也可以编码之后存），后者包含微地址给定部分和顺序控制方式指出下一条指令应如何找到；
微地址形成电路. 根据顺序控制字段给出的微地址给定部分、顺序控制方式，以及 机器指令代码、机器运行状态 形成下一条指令的微地址；
微地址寄存器. 保存微指令对应的微地址，指向对应的 CM。

本质上这就是你把状态机的内容写在了 ROM 里，然后做了一个模拟状态机的程序。

这种控制器执行机器指令时，会：

从存储控制器中读取“取机器指令用的微指令”，然后执行该微程序；
根据 IR 中的 opcode，经微地址形成电路，找到该指令对应的微程序入口，执行完该程序；
回到“取机器指令用的微指令”，重复。

为什么顺序控制字段包含一个控制方式和一个给定部分？这是因为如此一来我们可以完成这种操作：

若顺序控制方式为 $0$，直接转移到微地址给定部分。
若顺序控制方式为 $1$，转移到 xx:微地址给定部分的后几位，其中 xx 藏在操作码中。
…

这样可以优化 ROM 的大小。这种控制器的优缺点如下：

缺点. 慢；
优点. 线路规整，灵活（方便增加指令）。