Revision | 密码学基础(上)
Introduction
Classic Cryptography
历史。考了就吃。
Perfectly Secret Cryptography
现代密码学对加密方案(Encryption Scheme)作如下形式化定义:
定义 1.2.1(Encryption Scheme). 一个 encryption scheme $\Pi$ 包含以下资料:
- 集合 $\mathscr{K}$,称为密钥空间;
- 集合 $\mathscr{M}$,称为消息空间;
- 集合 $\mathcal{C}$,称为密文空间;
- 算法 $\mathsf{Enc}: \mathscr{K}\times \mathscr{M}\rightarrow \mathscr{C}$,称为加密函数;
- 算法 $\mathsf{Dec}: \mathscr{K}\times \mathscr{C}\rightarrow \mathscr{M}$,称为解密函数;
- 算法 $\mathsf{Gen} : \mathscr{K}$,称为密钥生成函数。记随机变量 $K\sim\mathsf{Gen}$,表示密钥。
此处 $\mathsf{Enc}, \mathsf{Dec}, \mathsf{Gen}$ 都可以是随机算法。
我们期待一个加密方案是正确且安全的。正确性之形式化是自然的。
定义 1.2.2(Perfect Correctness). 称一个 encryption scheme $\Pi = (\mathscr{K}, \mathscr{M}, \mathscr{C}, \mathsf{Enc}, \mathsf{Dec}, \mathsf{Gen})$ 具有 perfect correctness 性质,当且仅当:
$$
\forall k\in \mathscr{K}, m\in \mathscr{M}, \quad \Pr[\mathsf{Dec}_k(\mathsf{Enc}_k(m)) = m] = 1
$$
而安全性自然是希望密码能够抵御各种攻击,如:
- Key Recovery Attack. 从 $c$ 中猜出 $k$;
- Message Recovery Attack. 从 $c$ 中猜出 $m$;
- ……
最理想的情况下,我们期待一个攻击者 Eve 从 $m$ 中无法得出任何信息。此处有三种殊途同归的形式化方法,其直觉分别为:
- 攻击者即使看见了密文,对“关于消息 $m$ 的信息 $f$”之了解程度也不多于瞎猜;
- 消息和密文独立;
- 攻击者无法区分密文是由哪条消息加密而来。
形式化定义如下
定义 1.2.3$^1$(Perfect Semantic Secrecy). 称 $\Pi$ 具有 Perfect Semantic Secrecy 性质,若对于任意 $\mathscr{M}$ 上的概率分布 $\mathrm{P}$ 任意的集合 $\Omega$、任意的攻击者 $\mathsf{Eve}: \mathscr{C}\rightarrow \Omega$ 和谓词 $f : \mathscr{M}\rightarrow \Omega$,都存在一个看不到密文的攻击者 $\mathsf{Eve}^D : \Omega$ 满足
$$
\Pr_{m\sim \mathrm{P}}[\mathsf{Eve}(\mathsf{Enc}_k(m)) = f(m)] = \Pr_{m\sim \mathrm{P}}[\mathsf{Eve}^D = f(m)]
$$
定义 1.2.3$^2$(Perfect Secrecy). 称 $\Pi$ 具有 Perfect Secrecy 性质,若对于任意 $\mathscr{M}$ 上的概率分布 $\mathrm{P}$,都有
$$
\forall \alpha\in \mathscr{M}, \beta\in \mathscr{C}, \quad \Pr_{m\sim \mathrm{P}}[m = \alpha] = \Pr_{m\sim \mathrm{P}, c = \mathsf{Enc}_K(m)}[m = \alpha | c = \beta]
$$
定义 1.2.3$^3$(Perfect Adversarial Indistinguishability). 定义 Distinguishability Game 为如下的交互过程:其中 adversary 持有一个算法 $\mathcal{A}: \mathscr{M}\times \mathscr{M}\times \mathscr{C}\rightarrow \{0, 1\}$,challenger 持有加密方案 $\Pi$:
| Round | Adversary | Challenger |
|---|---|---|
| 1 | 选定 $m_0, m_1\in \mathscr{M}$,发送给 Dealer | |
| 2 | 采样 $k\sim \mathsf{Gen}, b\sim \mathrm{Bern}(1/2)$ 发送 $c = \mathsf{Enc}_k(m_b)$ 给 adversary |
|
| 3 | 猜测 $\hat{b} = \mathcal{A}(m_0, m_1, c)$ |
称 adversary 赢了这个游戏,若 $\hat{b} = b$,记作事件 $\mathsf{PrivK}_{\mathcal{A}, \Pi}$。
称 $\Pi$ 具有 Perfect Adversarial Indistinguishability 性质,若对于任意的算法 $\mathcal{A}$,都有
$$
\Pr[\mathsf{PrivK}_{\mathcal{A}, \Pi}] \leq \frac 12
$$
定理 1.2.1. 定义 1.2.3$^{1}$,1.2.3$^2$,1.2.3$^3$ 等价。
证明.
Perfect Secrecy $\Rightarrow$ Perfect Semantic Secrecy. 注意到
$$
\Pr[C = c | M = m] = \frac{\Pr[M = m | C = c]\Pr[C = c]}{\Pr[M = m]} = \Pr[C = c]
$$
即 $m$ 和 $\mathsf{Enc}_k(m)$ 独立。因此 $\mathsf{Eve}^D$ 只需要自己 sample $C$,即可获得与 $\mathsf{Eve}$ 同分布的输出。
Perfect Semantic Secrecy $\Rightarrow$ Perfect Adversarial Indistinguishability. 取 $\mathrm{P}$ 为 $m_0, m_1$ 上的均匀分布,$f$ 为 $m_b \mapsto b$ 易见。
Perfect Adversarial Indistinguishability $\Rightarrow$ Perfect Secrecy. 注意 indistinguishability 蕴含
$$
\forall m_0, m_1\in \mathscr{M}, c\in \mathscr{C}, \quad \Pr[C = c | M = m_0] = \Pr[C = c | M = m_1]
$$
将 $m_1$ 在 $\mathrm{P}$ 上累加后使用 Bayes 公式立即得证。
定理 1.2.2. 存在具有 perfect correctness 和 perfect secrecy 性质的 encryption scheme。
证明(One-time Pad). 令 $\mathscr{K} = \mathscr{C} = \mathscr{M}$ 为某一阿贝尔群。三个算法:
- $\mathsf{Gen}$ 为 $\mathscr{K}$ 上的均匀分布;
- $\mathsf{Enc}_k(m) = m + k$;
- $\mathsf{Dec}_k(m) = m - k$。
容易证明无论 $M$ 是什么,$C$ 都是均匀分布。
Private Key Cryptography
实践中,我们希望短密钥能够加密长消息。直观的想法是,放宽正确性和安全性的概率限制。对于 $\varepsilon \in (0, 1)$,我们可以得到
定义 2.0.1($\varepsilon$-Statistical Correctness). 称 $\Pi$ 是 $\varepsilon$-statistical correct 的,若
$$
\Pr[\textsf{Dec}_k(\textsf{Enc}_k(m)) = m] \geq 1 - \varepsilon
$$
定义 2.0.2($\varepsilon$-Statistical Semantic Secrecy). 称 $\Pi$ 是 $\varepsilon$-statistical semantic secret 的,若对于任意 $\mathscr{M}$ 上的概率分布 $\mathrm{P}$ 任意的集合 $\Omega$、任意的攻击者 $\mathsf{Eve}: \mathscr{C}\rightarrow \Omega$ 和谓词 $f : \mathscr{M}\rightarrow \Omega$,都存在一个看不到密文的攻击者 $\mathsf{Eve}^D : \Omega$ 满足
$$
|\Pr_{m\sim \mathrm{P}}[\mathsf{Eve}(\mathsf{Enc}_k(m)) = f(m)] - \Pr_{m\sim \mathrm{P}}[\mathsf{Eve}^D = f(m)]| < \varepsilon
$$
定义 2.0.3($\varepsilon$-Statistical Secrecy). 称 $\Pi$ 是 $\varepsilon$-statistical secret 的,若对于任意的 $m_0, m_1$,都有
$$
\Delta_{TV}(\textsf{Enc}_K(m_0), \textsf{Enc}_K(m_1)) \leq \varepsilon
$$
定义 2.0.4($\varepsilon$-Statistical Indistinguishability)。 称 $\Pi$ 是 $\varepsilon$-statistical indistinguishable 的,若对于任意的 $\mathcal{A}$,都有
$$
\Pr[\textsf{PrivK}_{\mathcal{A}, \Pi}] \leq \frac 12(1 + \varepsilon)
$$
Remark. 以上尝试均只是杯水车薪。可以证明:
- Statistical semantic secrecy,statistical secrecy,statistical indistinguishability 相互等价;
- 满足 statistical secrecy 和 perfect correctness 的 encryption scheme 中 $|\mathscr{K}| / |\mathscr{M}|$ 之下界为 $1 - \varepsilon$;
- 满足 statistical correctness 和 perfect secrecy,且 $\mathsf{Enc}$ 和 $\mathsf{Dec}$ 均为确定性算法的 encryption scheme 中 $|\mathscr{K}| / |\mathscr{M}|$ 之下界为 $1 - \varepsilon$。
而且这些界都是紧的,即确实存在相应的 encryption scheme。
因此,必须对安全性的定义再做进一步的让步。接下来我们将会发现,限制前文所述所有算法的计算能力(攻击者必须是高效的算法),即可让缩短密钥长度称为可能。
Computational Security
此后我们以「p.p.t」代指多项式时间随机(算法),即 probabilistic polynomial time。本节如果没有特别说明,所谓“算法”都是 non-uniform 的(i.e. 电路族 / 带多项式长度建议的算法),毕竟现实中攻击某个密码可以对于每个长度逐个击破。
我们接下来将会从两个方面放松安全性条件:
- 要求所有算法都是高效的(i.e. p.p.t);
- 容许攻击以可忽略的概率成功。
首先规定何种概率是“可忽略的”。
定义 2.1.1(Negligible Function). 函数 $\mathrm{negl}(n)$ 被称为可忽略的,若对于任意的 $k$,都有
$$
\mathrm{negl}(n) = o(n^{-k})
$$
这是一个介于多项式级别递减和指数级递减之间的一种递减速度。接下来加密方案的定义将被修正为
定义 2.1.2(Private-Key Encryption Scheme). 一个 private-key encryption scheme $\Pi$ 包含以下资料:
- p.p.t 算法 $\textsf{Gen}$。该算法输入 $1^\lambda$ 之后输出一个密钥 $k$,其中 $|k|\geq \lambda$。
- p.p.t 算法 $\textsf{Enc}$。该算法输入 $k, m$ 之后输出密文 $c$。
- p.p.t 算法 $\textsf{Dec}$。该算法输入 $k, c$ 之后输出原文 $m$。
$\Pi$ 必须是正确的。即对于任意的 $k \leftarrow \mathsf{Gen}(1^\lambda)$ 和 $m$,必须有 $\textsf{Dec}_k(\textsf{Enc}_k(m)) = m$。
通常情况下,我们考虑的加密方案都满足这些附加条件:
- $\textsf{Gen}(1^\lambda)$ 的输出服从 ${0, 1}^n$ 上的均匀分布。
- $\textsf{Enc}_k(m)$ 只加密 $|m| = \ell(|k|)$ 的消息。此处 $\ell$ 是一个多项式时间可计算的函数。
以后,这样的加密方案称为 $\ell$-private-key encryption scheme
现在定义计算安全性。Perfect Secrecy 似乎比较没救,这里都不采用。
定义 2.1.3$^1$(Computational Indistinguishability). 考虑如下参数化的 Indistinguishability Game($\textsf{PrivK}_{\mathcal{A}, \Pi}(\lambda)$):
| Round | Adversary | Challenger |
|---|---|---|
| 1 | 用多项式时间,在 $1^\lambda$ 上计算 $m_0, m_1$(满足 $|m_0| = |m_1| = \ell(\lambda)$),发送给 Dealer | |
| 2 | 采样 $k\sim \mathsf{Gen}(1^\lambda), b\sim \mathrm{Bern}(1/2)$ 发送 $c = \mathsf{Enc}_k(m_b)$ 给 Challenger |
|
| 3 | 猜测 $\hat{b} = \mathcal{D}(c, 1^\lambda)$ |
称加密方案 $\Pi$ 满足 Computational Indistinguishability,若对于任意的 p.p.t distinguisher $\mathcal{D}$,都存在一个 negligible function $\mathrm{negl}(n)$ 使得对于任意的 $\lambda$,
$$
\Pr\left[\textsf{PrivK}_{\mathcal{A}, \Pi}(\lambda)\right] \leq \frac 12 + \mathrm{negl}(\lambda)
$$
以及相应的 Semantic Secrecy:
定义 2.1.3$^2$(Computational Semantic Security). 若对于任意 $\lambda$,$\{0, 1\}^{\ell(\lambda)}$ 上的概率分布 $\mathrm{P}$,可用多项式时间算法刻画的谓词 $f : \{0, 1\}^{\ell(\lambda)}\rightarrow \Omega$,p.p.t adversary $\mathcal{A}$,都存在一个 negligible function $\mathrm{negl}(n)$ 和 p.p.t 算法 $\mathcal{A}’$ 使得
$$
\left|\Pr[\mathcal{A}(1^\lambda, c) = f(m)] - \Pr[\mathcal{A}’(1^\lambda) = f(m)]\right| \leq \mathrm{negl}(\lambda)
$$
定理 2.1.1. 定义 2.1.3$^1$ 等价于定义 2.1.3$^2$。
证明(Sketch).
Computational indistinguishability 蕴含 computational semantic security 显然的。这里重点证明反方向结论。
施反证法。假设不存在 p.p.t distinguisher,但是存在谓词 $f$,分布 $\mathrm{P}$ 和 p.p.t 算法 $\mathcal{A}$,使得对于任意的 $\mathcal{A}’$ 都有
$$
|\Pr[\mathcal{A}(1^\lambda, c) = f(m)] - \Pr[\mathcal{A}’(1^\lambda) = f(m)]| > \frac{1}{\lambda^k}
$$
对于无穷多个 $\lambda$ 成立。任选 $m_0$,取 $\mathcal{A}’$ 为如下算法:
- 在输入 $1^\lambda$ 上:
- 采样 $k\leftarrow \textsf{Gen}(1^\lambda)$;
- 输出 $\mathcal{A}(1^\lambda, \textsf{Enc}(k, m_0))$。
根据 probabilistic method 经典结论,必存在一系列 $m_1$ 使得
$$
|\Pr[\mathcal{A}(1^\lambda, \mathsf{Enc}_k(m_1)) = f(m_1)] - \Pr[\mathcal{A}’(1^\lambda) = f(m_1)]| > \frac{1}{\lambda^k}
$$
对无穷多个 $\lambda$ 成立。考虑如下的算法 $\mathcal{D}^1$:
- 在输入 $c, 1^\lambda$ 上:
- 计算 $y \leftarrow \mathcal{A}(, 1^\lambda)$;
- 若 $y = f(m_1)$,输出 $1$;否则输出 $0$。
若 $b = 1$,算法输出 $1$ 的概率为 $\Pr[\mathcal{A}(1^\lambda, c) = f(m_1)]$;若 $b = 0$,算法输出 $1$ 的概率为 $\Pr[\mathcal{A}(1^\lambda) = f(m_1)]$。这两个概率之间存在 $1 / \lambda^k$ 的 separation,因此通过重复多项式次 $\mathcal{D}$ 采样估计概率,判断和重复运行 $\mathcal{A}’$ 得到 $f(m_1)$ 的概率是否相近,从而做出一个 distinguisher。
Remark. 实际上这里有一个要点是高效找到 $m_1$。我们的做法是直接随机,看起来多项式次随机总能打中一个概率 separation 大的?
本节末尾,我们展示密钥长度远小于消息长度的安全的加密方案之存在性依赖于 $\mathbf{P} \ne \mathbf{NP}$。
定理 2.1.2. 若 $\mathbf{P} = \mathbf{NP}$,则不存在 computational indistinguishable 的 encryption scheme,其 $\mathsf{Enc}$ 和 $\mathsf{Dec}$ 都是确定性算法,且 $\ell(\lambda) > 2\lambda$。
证明.
关于 $\ell$ 的限制相当于 $|\mathscr{K}|^2 < |\mathscr{M}|$。
任取一条消息 $m_0$。它用 $|\mathscr{K}|$ 个密钥加密得到 $|\mathscr{K}|$ 个密文,这 $|\mathscr{K}|$ 个密文解码之后共计可能有 $|\mathscr{K}|^2$ 种消息。然而 $|\mathscr{K}|^2 < |\mathscr{M}|$,因此存在一个 $m_1$,使得
$$
\{\textsf{Enc}_k(m_0) : k\in \mathscr{K}\} \cap \{\textsf{Enc}_k(m_1) : k \in \mathscr{K}\} = \varnothing
$$
那么 distinguisher 无非是要判定这样一个问题:
$$
\exists k, \textsf{Enc}_k(m_1) = c
$$
这是一个 $\mathbf{NP}$ 问题,根据假设也是一个 $\mathbf{P}$ 问题,因此 distinguisher 存在。
欲构造 computational indistinguishable 的 encryption scheme,一个直接的想法是推广 one-time pad。此时亟需用少量随机种子生成长随机串,因此我们定义 PseudoRandom Generator:
定义 2.1.4(Pseudorandom Generator). 令 $\ell(n)$ 是一个多项式。确定性多项式大小电路族 $\mathcal{G}(n)$ 被称为 $\ell(n)$-PRG,若对于任意 p.p.t distinguisher $\mathcal{D}$(也是多项式大小电路族 / 带多项式建议的算法),都存在一个 negligible function $\mathrm{negl}(n)$ 使得
$$
\left\lvert\Pr_{s\sim \mathrm{Uniform}(2^n)}[\mathcal{D}(\mathcal{G}(s))] - \Pr_{r\sim \mathrm{Uniform}(2^{\ell(n)})}\left[\mathcal{D}(r) = 1\right]\right\rvert \leq \mathrm{negl}(n)
$$
Remark. 该定义比计算理论中的 PRG 定义弱。计算理论中仅要求 PRG 是 $\mathbf{P}/\mathrm{poly}$ 的算法,我们这里要求它是 $\mathbf{P}$ 的。
一旦存在 PRG,便可构造 computational indistinguishable 的 encryption scheme:
定理 2.1.3. 若存在 $\ell$-PRG $\mathcal{G}$,则存在 computational indistinguishable 的 $\ell$-private-key encryption scheme。
证明(One-Time Pad). $\textsf{Enc}_k(m) = m \oplus \mathcal{G}(k)$,$\textsf{Dec}_k(c) = c \oplus \mathcal{G}(k)$。
如能 distinguish 这个 encryption scheme,必能 distinguish 该 PRG,矛盾。
Extend to Multi-message
然而,One-Time Pad,顾名思义,仅能进行一轮通信。不妨将 indistinguishability 之定义拓展至多消息:
定义 2.2.1(Multi-message Indistinguishability) $\textsf{PrivK}_{\mathcal{A}, \Pi}^{\text{multi-msg}}(\lambda)$ 流程如下,Adversary 是一个具有如下模板的多项式电路族,其胜利当且仅当猜对 $b$:
| Round | Adversary | Challenger |
|---|---|---|
| 1 | 用多项式时间,在 $1^\lambda$ 上计算两列 $m_0^i, m_1^i$ ($i = 1, 2, …, t$),发送给 Dealer | |
| 2 | 采样 $k\sim \mathsf{Gen}(1^\lambda), b\sim \mathrm{Bern}(1/2)$ 发送 $c = \mathsf{Enc}_k(m_b)$ 给 Adversary |
|
| 3 | 猜测 $\hat{b} = \mathcal{A}(c, 1^\lambda)$ |
称加密方案 $\Pi$ 满足 multi-message security,若存在 negligble funcion $\mathrm{negl}(n)$ 使得
$$
\Pr\left[\textsf{PrivK}_{\mathcal{A}, \Pi}^{\text{multi-msg}}(\lambda)\right] \leq \frac 12 + \mathrm{negl}(\lambda)
$$
我们可以将多消息加密方案分为两类:
- 状态有关. 加密、解密算法内置一个状态机,每加密一条消息,做相应转移;
- 状态无关. 加密、解密算法对任何时间的输入都一视同仁。
下方罗列的几个构造,均有各自的问题:
尝试 2.2.1(状态无关确定性加解密算法). 任意的状态无关的加密方案,其中 $\mathsf{Enc}$ 和 $\mathsf{Dec}$ 都是确定性算法。
攻击. 考虑取 $m_0^1 = m_0^2 = \$, m_1^1 = \$, m_2^1 = \$$。其中 $\$$ 指独立随机采样(今后也将使用此记号)。如果 $c^1 = c^2$,猜 $b = 0$;否则猜 $b = 1$。
对于尝试 2.2.1 中所给的算法,我们可以将其抽象成如下的伪随机排列(PseudoRandom Permutation)。
定义 2.2.2(Pseudorandom Permutation). 函数 $\mathcal{F}: \{0, 1\}^\lambda\times \{0, 1\}^{\ell(\lambda)}\rightarrow \{0, 1\}^{\ell(\lambda)}$ 是 PRP 当且仅当:
- $\mathcal{F}_k$ 和 $\mathcal{F}_k^{-1}$ 都是多项式时间可计算的。
- 对于任意的 p.p.t oracle distinguisher $\mathcal{D}^{\mathcal{O}}$,都有
$$
\left|\Pr_{k}\left[\mathcal{D}^{\mathcal{F}(k, \cdot)}(1^\lambda) = 1\right] - \Pr_f\left[\mathcal{D}^{f(\cdot)}(1^\lambda) = 1\right]\right| < \mathrm{negl}(\lambda)
$$
其中 $f$ 从全体 $\{0, 1\}^{\ell(\lambda)}\rightarrow \{0, 1\}^{\ell(\lambda)}$ 的排列中均匀随机抽取。特别地,若允许 $\mathcal{D}$ 调用逆函数,即
$$
\left|\Pr_{k}\left[\mathcal{D}^{\mathcal{F}(k, \cdot), \mathcal{F}^{-1}(k, \cdot)}(1^\lambda) = 1\right] - \Pr_f\left[\mathcal{D}^{f(\cdot), f^{-1}(\cdot)}(1^\lambda) = 1\right]\right| < \mathrm{negl}(\lambda)
$$
则 $\mathcal{F}$ 称为强 PRP。
尝试 2.2.2(Stream Cipher). 这是一种状态有关的加密方案。基于一个 $\ell(n)T$-PRG $\mathcal{G}$,记
$$
\mathcal{G}(s) = r_1 \Vert r_2 \Vert \cdots \Vert r_T
$$
其中,$|r_i| = \ell(n)$,我们可以令:
$$
\mathsf{Enc}(m^i) = m^i \oplus \mathcal{G}(k)_i
$$
该加密方案确实是 multi-message indistinguishable 的,可惜实践中我们希望加密方案是状态无关的。
尝试 2.2.3(一个状态无关的尝试). 基于一个 $\ell(n)T$-PRG $\mathcal{G}$,同样将其输出记作上方的 slice 形式。考虑 $\mathsf{Enc}$ 为如下算法,对应的 $\mathsf{Dec}$ 是容易写出的:
- 采样 $r \sim \mathrm{Uniform}([T])$;
- 输出 $(r, \mathcal{G}(k)_r)$。
攻击. 这里 $T$ 必须是多项式大小的,否则算不动。若 $T$ 是多项式大小的,则可以进行生日悖论攻击:令 $m_0^1, …, m_0^{\sqrt T} = \$, m_1^i = \$$。若发现返回的密文不是两两不同的,猜 $b = 0$;否则猜 $b = 1$。
如果能将尝试 2.2.3 中的 $T$ 拓展至指数级,那么生日悖论攻击将不再成立。此时,我们需要一个结构是 PseudoRandom Function:
定义 2.2.3(Pseudorandom Function). 满足如下条件的确定性多项式大小电路族 $\mathcal{F}: \{0, 1\}^\lambda \rightarrow \{0, 1\}^{\ell_1(\lambda)}\rightarrow \{0, 1\}^{\ell_2(\lambda)}$ 被称为一个 $(\ell_1, \ell_2)$-PRF 当且仅当对于带 oracle 访问的 p.p.t 算法 $\mathcal{D}^{\mathcal{O}}$(上指标表示该算法对 oracle $\mathcal{O}$ 有访问权限),都存在 negligible function $\mathrm{negl}(n)$ 使得
$$
\left|\Pr_{k}\left[\mathcal{D}^{\mathcal{F}(k, \cdot)}(1^\lambda) = 1\right] - \Pr_f\left[\mathcal{D}^{f(\cdot)}(1^\lambda) = 1\right]\right| < \mathrm{negl}(\lambda)
$$
其中 $f$ 从全体 $\{0, 1\}^{\ell_1(\lambda)}\rightarrow \{0, 1\}^{\ell_2(\lambda)}$ 的函数中均匀随机抽取(下文中方便起见,称为纯随机函数)。
定理 2.2.1. 存在 $(\lambda, \ell(\lambda))$-PRF,便存在状态无关的 multi-message indistinguishable 加密方案。
证明. $\Pi$ 的 $\mathsf{Enc}$ 为如下算法,对应的 $\mathsf{Dec}$ 是容易写出的:
- 采样 $r \sim \mathrm{Uniform}(2^\lambda)$;
- 输出 $(r, \mathcal{F}(k, r))$。
下证其安全性。考虑另一个加密方案 $\Pi’$,和 $\Pi$ 的唯一区别是将 PRF 换成纯随机函数。那么,任意的 adversary $\mathcal{A}$ 都只是收到一堆独立随机的数,$\Pr[\mathsf{PrivK}_{\Pi’, \mathcal{A}}^{\text{multi-msg}}] \leq \frac 12$。由于 $\mathcal{F}$ 是个 PRF,必有 $\Pr[\mathsf{PrivK}_{\Pi, \mathcal{A}}^{\text{multi-msg}}] \leq \frac 12 + \mathrm{negl}(\lambda)$,否则 indistinguishability game 的流程稍加改造便可作为 $\mathcal{F}$ 的 distinguisher。
最后,常见的通信场景是使用某确定长度的加密方案(比如 AES-128)加密任意长度的消息,且有多次发送。此时,除了使用 Stream Cipher,有以下几种状态无关的基于给定的 PRF / encryption scheme 的做法,统称为 Block Cipher 的几种加密模式(Mode of Operations):
Electronic Code Book (ECB). 设 $\mathsf{Enc}$ 是 multi-message indistinguishable 的加密函数。
- 在输入 $m^1, …, m^t$ 上:
- 输出 $\mathsf{Enc}_k(m^1), …, \mathsf{Enc}_k(m^t)$。
Cipher Book Chaining (CBC). 给定一个安全的 $\mathsf{Enc}$,本模式的 $\mathsf{Enc}$ 如下,相应 $\mathsf{Dec}$ 的编写是容易的。
- 在输入 $m^1, …, m^t$ 上:
- 随机采样 $\mathrm{IV}\sim \mathrm{Uniform}(2^{\ell(\lambda)})$,置 $c_0 = \mathrm{IV}$;
- For $i = 1, 2, …, t$:
- $\qquad$ $c_i \leftarrow \mathsf{Enc}_k(c_{i - 1}\oplus m^i)$;
- 输出 $c_0, …, c_t$。
Remark. 这个模式其实没那么安全。很明显他防不住 CPA(定义见下一节),所以我不知道怎么讲。
Output Feedback (OFB). 给定 PRF $\mathcal{F}$。$\mathsf{Enc}$ 如下,相应的 $\mathsf{Dec}$ 的编写是容易的。
- 在输入 $m^1, …, m^t$ 上:
- 随机采样 $\mathrm{IV}\sim \mathrm{Uniform}(2^{\ell(\lambda)})$,置 $y_0 = c_0 = \mathrm{IV}$;
- For $i = 1, 2, …, t$:
- $\qquad$ $y_i \leftarrow \mathcal{F}_k(y_{i - 1})$;
- $\qquad$ $c_i \leftarrow y_i \oplus m_i$;
- 输出 $c_0, …, c_t$。
Counter(CTR). 给定 PRF $\mathcal{F}$。$\mathsf{Enc}$ 如下,相应的 $\mathsf{Dec}$ 的编写是容易的。
- 在输入 $m^1, …, m^t$ 上:
- 随机采样 $\mathrm{IV}\sim \mathrm{Uniform}(2^{\ell(\lambda)})$,置 $c_0 = \mathrm{IV}$;
- For $i = 1, 2, …, t$:
- $\qquad$ $c_i = m_i\oplus \mathcal{F}_k(\mathrm{IV} + i - 1)$。
- 输出 $c_0, …, c_t$。
CPA-Security
如果泄露了 $\mathsf{Enc}$ 的接口,密码是否仍然安全?在此情况下,攻击者可以对密码实施选择明文攻击(Chosen Plaintext Attack),为此定义相应的安全性:
定义 2.3.1(CPA-Security). 考虑如下的安全性游戏 $\mathsf{PrivK}_{\Pi, \mathcal{A}}^{\mathrm{CPA}}$:
| Stage | Adversary | Challenger |
|---|---|---|
| 1 | 多项式轮,询问 $\hat{m}_i$ 的密文 | 回答 $\hat{m}_i$ 的密文 |
| 2 | 发送 $m_0, m_1$ 给 Challenger | |
| 3 | 采样 $k\sim \mathsf{Gen}(1^\lambda), b\sim \mathrm{Bern}(1/2)$ 发送 $c = \mathsf{Enc}_k(m_b)$ 给 Adversary |
|
| 4 | 多项式轮,询问 $\hat{m}_i$ 的密文 | 回答 $\hat{m}_i$ 的密文 |
| 5 | 猜测 $\hat{b} = \mathcal{A}(c, 1^\lambda)$ |
称 $\Pi$ 是 CPA-Secure 的,当且仅当对于任意的 p.p.t adversary $\mathcal{A}$,都存在 negligble function $\mathrm{negl}$ 使得
$$
\Pr\left[\textsf{PrivK}_{\mathcal{A}, \Pi}^{\mathrm{CPA}}(\lambda)\right] \leq \frac 12 + \mathrm{negl}(\lambda)
$$
当然,你在提出 $m_0, m_1$ 的时候,是禁止提出已经问过或将要询问的东西的,不然就没有意义了。
定理 2.3.1. 存在 indistinguishable,但是没有 CPA 安全性的密码。
证明(Backdoor Attack). 假设存在 indistinguishable encryption scheme $\Pi = (\mathsf{Enc}, \mathsf{Dec})$。构造如下加密方案 $\Pi’ = (\mathsf{Enc}’, \mathsf{Dec}’)$:
- 将密钥 $k$ 视作 $k’\Vert r’$,分割线位于正中央。
- 令 $\mathsf{Enc}’$ 为
$$
\mathsf{Enc}’_k(x\Vert t) = \begin{cases}
\mathsf{Enc}_{k’}(x) \Vert r’ & t \ne r’ \\
k & t = r’
\end{cases}
$$
$\Pi’$ 显然是 indistinguishable 的,因为只有一轮交互 w.h.p 猜不到 $r’$。但是若可以进行 CPA,就可以通过预先询问套出密钥 $k$。
之所以在 CPA 定义中仅仅发送 $m_0, m_1$ 而不是两列明文,是因为直觉上既然能事先事后多次询问,那么区分两个明文和两列明文的难度应当完全一致。形式化地,
定理 2.3.2. 将上述 CPA Game 的 stage 2 修改作
Adversary:发送两列 $m_0^i, m_1^i$ 给 Challenger
得到另一种 CPA Game $\mathsf{PrivK}_{\mathcal{A}, \Pi}^{\mathrm{LR-CPA}}$ 和相应的安全性(暂时称为 CPA$^{\dagger}$ Secure)。则有 CPA Secure 等价于 CPA$^{\dagger}$ Secure。
这里的安全性游戏本质上是 $\mathcal{A}$ 可以访问一个 oracle $\mathrm{LR}_b(m_0, m_1)$,challenger 会将 $\mathsf{Enc}_k(m_b)$ 答复给 $\mathcal{A}$,最后 $\mathcal{A}$ 猜测 $b$。以后我们将分析这个等价的游戏。
证明(Hybrid Argument).
CPA$^\dagger$ Secure 蕴含 CPA Secure 是显然的。此处着重证明反向的结论。考虑任意一个 CPA$^\dagger$ Game 的 Adversary $\mathcal{A}’$。在其基础上构造 $\mathcal{A}$:
- 模拟 $\mathcal{A}’$ 的同时:
- 随机采样 $i\sim \mathrm{Uniform}([T])$,其中 $T$ 为 $\mathcal{A}$ 的询问次数上界;
- 对于 $\mathcal{A}’$ 的第 $j$ 次对 $\mathrm{LR}_b$ 的访问:
- $\qquad$ 若 $j < i$,查询 $\mathsf{Enc}_k(m_0^j)$ 并发送给 $\mathcal{A}’$;
- $\qquad$ 若 $j = i$,给 challenger 发送 $(m_0^i, m_1^i)$,将 challenger 的回复转发给 $\mathcal{A}’$;
- $\qquad$ 若 $j > i$,查询 $\mathsf{Enc}_k(m_0^j)$ 并发送给 $\mathcal{A}’$。
- 猜测结果 $b$ 为 $\mathcal{A}’$ 的最终输出。
由于对于任意的固定的 $i$,$\mathcal{A}$ 都是一个 CPA Game 的 Adversary,由于 $\Pi$ 是 CPA Secure 的,我们有
$$
\forall \hat{i},\quad \left|\Pr[\mathcal{A} \rightarrow 0 | i = \hat{i}, b = 0] - \Pr[\mathcal{A} \rightarrow 0 | i = \hat{i}, b = 0]\right| \leq \mathrm{negl}(\lambda)
$$
现在考虑一系列虚拟的安全性游戏:$\mathrm{Hybrid}^0_{\mathcal{A}’, \Pi}, …, \mathrm{Hybrid}^{T - 1}_{\mathcal{A}’, \Pi}$。其中在游戏 $\mathrm{Hybrid}^i_{\mathcal{A}’, \Pi}$ 中,$\mathcal{A}’$ 将会有机会访问 oracle $\mathrm{LR}_b^i(m_0, m_1)$:该 oracle 将会在前 $i - 1$ 次询问时回答 $\mathsf{Enc}_k(m_0)$,第 $i$ 次回答 $\mathsf{Enc}_k(m_b)$,以后回答 $\mathsf{Enc}_k(m_1)$。注意,$\mathrm{LR}_1^i = \mathrm{LR}_0^{i + 1}$,因此有:
$$
\begin{align}
\Pr[\mathsf{PrivK}_{\mathcal{A’}, \Pi}^{\text{LR-CPA}}] &= \frac 12 + \left|\Pr\left[\mathcal{A}’^{\mathrm{LR}_b}\rightarrow 0 | b = 0\right] - \Pr\left[\mathcal{A}’^{\mathrm{LR}_b}\rightarrow 0 | b = 1\right]\right| \\
&= \frac 12 + \left|\Pr\left[\mathcal{A}’^{\mathrm{LR}_b^0}\rightarrow 0 | b = 0\right] - \Pr\left[\mathcal{A}’^{\mathrm{LR}_b^{T - 1}}\rightarrow 0 | b = 1\right]\right| \\
&= \frac 12 + \left|\sum_{i=0}^{T - 1}\Pr\left[\mathcal{A}’^{\mathrm{LR}_b^i}\rightarrow 0 | b = 0\right] - \Pr\left[\mathcal{A}’^{\mathrm{LR}_b^i}\rightarrow 0 | b = 1\right]\right| \\
&\leq \frac 12 + \mathrm{negl}(\lambda)
\end{align}
$$
定理 2.2.1. 中构造证明就是 CPA 安全的。
CCA-Security,Message Authentication Code
如果你甚至泄露了 $\mathsf{Dec}$ 的接口,则攻击者可以进行 CCA 攻击。
定义 2.4.1(CCA-Security). 在 $\mathsf{PrivK}^{\mathcal{A, \Pi}^{\mathrm{CCA}}}$ 中,一个对 $\mathsf{Enc}$,$\mathsf{Dec}$ 有 oracle 访问权限的 adversary 需要在进行多项式次询问(Stage 1)之后提出 $m_0, m_1$(和此前询问均不相同,Stage 2),然后收到来自 challenger 的 $c_b$。之后,adversary 还可以进行若干询问(Stage 3),最后猜测 $b$。
如果 Stage 3 中只能访问 $\mathsf{Enc}$,所得安全性称为 CCA$^1$ Secure;若还能访问 $\mathsf{Dec}$,所得安全性称为 CCA$^2$ Secure。
我们之前的一切构造都不是 CCA Secure 的。要防御 CCA,一个直接的想法是让所有的 $\mathsf{Dec}$ 查询都失效。这样一来,原来是 CPA 安全的 encryption scheme 即变为 CCA 安全的。为此,考虑设计一个机制,使得 $\mathsf{Enc}$ 产生的消息能通过校验,但是 adversary 伪造的消息不能通过校验。形式化地,定义 Message Authentication Code:
定义 2.4.2(MAC). 一个 MAC scheme $\Pi$ 包含以下资料:
- $\mathsf{Gen}$:生成密钥;
- p.p.t 电路族 $\mathsf{MAC}(k, m)$:根据密钥 $t$ 和消息 $m$,输出一个标签 $t$;
- p.p.t 电路族 $\mathsf{Verify}(k, m, t)$:判断标签 $t$ 是否是由 $m$ 产生的合法标签。
一个 $\mathsf{MAC}$ 须满足:
- 正确性. 对于任意的 $k, m$ 有
$$
\Pr[\mathsf{Verify}(k, m, \mathsf{MAC}(k, m)) = 1] = 1
$$ - (强)不可伪造性. 对于任意的 p.p.t adversary $\mathcal{A}^{\textsf{Dec}_k}(1^{\lambda})$,存在 negligible function $\mathrm{negl}$,使得在 $\mathcal{A}$ 成功伪造一个新的$^1$ $(m, t)$,使得 $\mathsf{Verify}(k, m, t) = 1$ 的概率不超过 $\mathrm{negl}(\lambda)$。
$^1$:这里的“新的”有两种释义。假设你询问了一列 $(m_i, t_i)$。若要求 $m \ne m_i$,则称为不可伪造性。若仅要求 $(m, t)\ne (m_i, t_i)$,则称为强不可伪造性。
容易发现,如果 $\mathsf{MAC}$ 是确定性算法,则显然存在一种校验方法,称为标准校验(canonical $\mathsf{Verify}$ algorithm):直接判断是否有 $t = \mathsf{MAC}(k, m)$。对于这种确定性的 $\mathsf{MAC}$,不可伪造性即是强不可伪造性。
定理 2.4.1. 若存在 PRF,则存在 MAC。
证明. 假设存在 PRF $\mathcal{F}$,则明显 $\mathcal{F}$ 本身加上标准校验就是 MAC。
定理 2.4.2. 若存在 CPA 安全的 $\Pi_1$ 和 MAC $\Pi_2$,则存在 CCA$^1$ 安全的 $\Pi’$;进一步,若 $\Pi_2$ 是强 MAC,则 $\Pi’$ 是 CCA$^2$ 安全的。
证明. $\Pi’$ 的构造如下:
- $\mathsf{Gen}(1^k)$:独立地生成 $k_{\text{CPA}}$ 和 $k_{\text{MAC}}$;
- $\mathsf{Enc}((k_1, k_2), m)$:输出 $\mathsf{Enc}_{\mathrm{CPA}}(k_1, m), \mathsf{MAC}(\mathsf{Enc}_{\mathrm{CPA}}(k_1, m))$;
- $\mathsf{Dec}(k, (c, t))$:若 $\mathsf{Verify}(k, c, t) = 0$,输出 $\bot$,否则正常解密 $c$。
若 $\mathsf{MAC}$ 是安全的,一切 $\mathsf{Dec}$ 调用高概率收到 $\bot$,便无用。
Remark. 为了加深理解,这里展示两种错误的构造:
- 输出 $\mathsf{Enc}(k_1, m\Vert \mathsf{MAC}(k, m))$。注意这个 $\mathsf{MAC}$ 屁用没有。
- 输出 $\mathsf{MAC}(k_2, m)\Vert \mathsf{Enc}(k_1, m)$。注意没有任何限制规定 $\mathsf{MAC}$ 不能泄露消息。
事实上,我们构造的这个 $\Pi’$,不但是 CCA 安全的,而且是不可伪造的。即你不可能经过多项式次询问之后伪造一条使得 $\mathsf{Dec}$ 不输出 $\bot$ 和已经问过的 $m$ 的密文。满足这种条件的 encryption scheme 称作 Authenticated Encryption,属最理想的安全性。
最后,既然我们有多消息的 Block Cipher,也就需要多消息的 MAC。参考 Block Cipher 的 mode of operations,可以提出若干方案。这里我们首先展示三种正确的方法:
双密钥 CMC-MAC 设 $\mathcal{F}$ 是一个 PRF。
- 随机密钥 $k_1, k_2$;令 $v \leftarrow 0$;
- For $i = 1, 2, …, n - 1$:
- $\quad$ $v\leftarrow \mathcal{F}(k_1, m_i \oplus v)$;
- 输出 $t = \mathcal{F}(k_2, m_n\oplus v)$
NMAC. 设 $\mathcal{F}$ 是一个 PRF。
- 随机密钥 $k, k’$;
- For $i = 1, 2, …, n$:
- $\quad$ $k \leftarrow \mathcal{F}(k, m_i)$;
- 输出 $t = \mathcal{F}(k’, k)$。
PMAC. 设 $\mathcal{F}$ 是一个 PRF。
- 随机密钥 $k, k’, k’’$;
- 令
$$
s \leftarrow \bigoplus_{i=1}^m \mathcal{F}(k’, m + ik)
$$ - 输出 $t = \mathcal{F}(k’’, s)$。
这些构造的中心思想大同小异,都是首先用一个结构做出不碰撞的输出,然后过一个 PRF。证明安全性只需要着眼于“没有碰撞”,和 Ruby-Lackoff 定理(参见定理 3.2.5)中没有碰撞的证明大同小异。一切归结为找到一个抗碰撞哈希函数(Collision Resistant Hash Function)$\mathcal{H}$。那么,$\mathcal{F}\circ\mathcal{H}$ 就是一个安全的 MAC。
提到抗碰撞哈希函数,又不得不提一个经典的构造:Merkle-Damgard 变换。它将一个 $2n\mapsto n$ 的 CRHF 变成 $*\mapsto n$ 的 CRHF。形式化地,有
定理 2.4.3. 若存在 $2n \mapsto n$ 的 CRHF,则存在 $*\mapsto n$ 的 CRHF。
证明(Merkle-Damgard). 若存在 CRHF,则显然存在输出不包含 $0$ 的 CRHF $h$。则考虑哈希函数 $H$,定义为:
- 令 $v \leftarrow \mathrm{IV} = 0$;
- For $i = 1, 2, …, n$:
- $\qquad$ $v\leftarrow h(v\Vert m_i)$;
- 输出 $h(v, n)$。
容易证明这个确实是 CRHF。
Remark. IV 和 n 的加入分别防止了取前缀和取后缀的攻击,缺一不可。
为了加强理解,最后给出几个不安全的多消息 MAC 并给出攻击方法。
Unsafe Example 2.4.1(ECB Mode). 直接对每条消息分别作用 MAC。注意这样一来,询问 $t\leftarrow \mathsf{MAC}(m)$ 之后可以伪造 $(m\Vert m, t\Vert t)$。
将其改进为首先随机采样 $r$,然后把每条消息变成 $m_1 \Vert r\Vert n \Vert i$ 后对其作 ECB,就是安全的。
Unsafe Example 2.4.2(CBC Mode). 将双密钥 CBC 修改为只是用同一个密钥。
令 $\mathsf{MAC}(m_1m_2m_3) = t$,则注意到 $\mathsf{MAC}(m_1, m_2, m_3, m_4) = \mathsf{m_4\oplus t}$。询问一者,伪造另一者。
当然,你可以证明如果询问必须是前缀无关的,那么双密钥 CBC 就确实是安全的。这种 MAC 称为 Prefix-Free MAC。
Theoretical Constructions
针对前文使用的 PRG、PRF、PRP 等工具,我们将给出一系列构造。
One-Way Function
密码学中所用工具,归根结底具有一种“可以高效加密、难以高效解密”的性质。将具备此类性质的函数称为“单向函数(One-Way Function)”,形式化地定义如下:
定义 3.1.1(One-Way Function). 函数 $f : \{0, 1\}^*\rightarrow \{0, 1\}^*$ 是单向函数,当且仅当
- $f$ 可以给 $\mathbf{P} / \mathrm{poly}$ 的算法计算。
- 对于任意的 p.p.t adversary $\mathcal{A}$,有
$$
\Pr_{x\sim \mathrm{Uniform}(2^n)}\left[\mathcal{A}(1^n, f(x)) \in f^{-1}(f(x))\right] \leq \mathrm{negl}(n)
$$
上式中的 $\mathrm{negl}$ 被换成 $1 / \mathrm{poly}(n)$ 得到的函数称为 Weak OWF。
此类函数,还可进一步配备以下几个性质:
- 保长度(length-preserving). 即 $|f(x)| = |x|$ 总是成立;
- 双射. 如果 $f(x)$ 是保长度的双射,而且是 OWF,则 $f(x)$ 也称为 One-Way Permutation。
离散对数问题就是一个 OWP 的候选,质因数分解问题是 Weak OWF 的候选。事实上:
定理 3.1.1. 若存在 Weak OWF,则存在 OWF。
证明(Yao).
【FIXME】
函数的单向性意味着它能藏住关于输入的信息。为了此后的应用,我们想要找到它具体能藏住什么样的信息,因此定义
定义 3.1.2(Hardcore Predicate). 函数 $\mathsf{hc}: \{0, 1\}^*$ 被称为 $f$ 的一个 hardcore-predicate,当且仅当
- 它可以被一族多项式大小电路计算;
- 对于任意的 p.p.t adversary $\mathcal{A}$,$\mathcal{A}$ 对 $\mathsf{hc}$ 所知甚少:
$$
\Pr_{x\leftarrow \mathrm{Uniform}(2^n)}[\mathcal{A}(1^n, f(x)) = \mathsf{hc}(x)] \leq \frac 12 + \mathrm{negl}(n)
$$
可以证明,Hardcore Predicate 是存在的。
定理 3.1.2(Goldreich-Levin Theorem). 若存在 OWF(OWP),则存在能藏住 hardcore predicate $\mathsf{hc}$ 的 OWF(OWP)$g$。
我们首先给出 $g$ 和 $\mathsf{hc}$ 的构造。假设存在 OWF $f(x)$。令
$$
g(x\Vert r) = f(x)\Vert r, \quad \textsf{hc}(x\Vert r) = \langle x, r\rangle = \bigoplus_{i=1}^n x_ir_i \quad \text{where $|x| = |r| = n$}
$$
这显然是一个 OWF。接下来我们逐步发掘 G-L 定理的真相。先证明一个弱一点的结论:
引理 3.1.4. 不存在 p.p.t adversary $\mathcal{A}$ 使得
$$
\Pr_{x, y\sim \mathrm{Uniform}(2^n)}[\mathcal{A}(1^{2n}, x, f(y)) = \langle x, y\rangle] > \frac 34 + \frac{1}{p(n)}
$$
对无穷多个 $n$ 成立。其中 $p(n)$ 为任意多项式。
证明.
施反证法,我们将证明上述 $\mathcal{A}$ 存在蕴含 $f$ 不是 OWF。核心想法是如果你能算 $\langle x, y\rangle$ 和 $\langle x\oplus e_i, y\rangle$,你就能算出 $y$ 的第 $i$ 位。朝此目标前进,我们将证明
- 对于很大一部分 $y$,随机 $x$,猜对 $\langle x, y\rangle$ 的概率很大。
- 对于很大一部分 $y$,随机 $x$,同时猜对 $\langle x, y\rangle$ 和 $\langle x\oplus e_i, y\rangle$ 的概率很大。
形式化地:
断言 1. 定义
$$
S_n = \left\{y : \Pr_{x\sim\mathrm{Uniform}(2^n)}\left[\mathcal{A}(1^{2n}, x, f(y)) = \langle x, y\rangle\right] \geq \frac 34 + \frac{1}{2p(n)}\right\}
$$
则 $|S_n| \geq 2^n / 2p(n)$。
断言 1 的证明. 这无非是个 Markov 不等式。
断言 2. 定义
$$
S’_n = \left\{y : \forall i, \Pr_{x\sim \mathrm{Uniform}(2^n)}\left[\mathcal{A}(1^{2n}, x, f(y)) = \langle x, y\rangle \wedge \mathcal{A}(1^{2n}, x \oplus e_i, f(y)) = \langle x \oplus e_i, y\rangle\right] \geq \frac 12 + \frac{1}{p(n)}\right\}
$$
则 $|S’_n|\geq 2^n / 2p(n)$。
断言 2 的证明. 只需证明 $S_n \subseteq S’_n$。这无非是个 union bound(两边错的概率都不超过 $1/4 - \frac{1}{2p(n)}$)。
有了断言 2,我们可以构造 $f$ 的 adversary $\mathcal{A}$ 如下:
- 在输入 $f(y)$ 上:
- **For $i = 1, 2, …, n$**:
- $\qquad$ For $j = 1, 2, …, n p^2(n)$:
- $\qquad \qquad$ 随机 $x\sim \mathrm{Uniform}(2^n)$;
- $\qquad \qquad$ 令 $\hat{y}_{i,j} = \mathcal{A}(1^{2n}, x, f(y)) \oplus \mathcal{A}(1^{2n}, x\oplus e_i, f(y))$;
- $\qquad$ 取 $y_i\leftarrow \mathrm{Majority}(\hat{y}_i)$。
Chernoff Bound 告诉我们 $\hat{y}_{i, j}$ 里高概率有一半以上都是对的,union bound 告诉我们 $y_i$ 高概率全是对的。
上面的证明弱就弱在断言 2 的 union bound。回到原定理,我们用一种聪明的办法来 amplify 成功概率:
定理 3.1.2 的最终证明. 施反证法,假设存在 p.p.t adversary $\mathcal{A}$ 使得
$$
\Pr_{x, y\sim \mathrm{Uniform}(2^n)}[\mathcal{A}(1^{2n}, x, f(y)) = \langle x, y\rangle] > \frac 12 + \frac{1}{p(n)}
$$
由 Markov Bound 可知,定义集合
$$
S_n = \left\{y : \Pr_{x\sim\mathrm{Uniform}(2^n)}\left[\mathcal{A}(1^{2n}, x, f(y)) = \langle x, y\rangle\right] \geq \frac 12 + \frac{1}{2p(n)}\right\}
$$
有 $|S_n| > 2^n / 2p(n)$。
Remark 3.1.1. 如果在此照搬断言 2 的 union bound,你会得到 $\Pr[…] \geq 1/p(n)$,没什么作用。这里的主要矛盾是 $x$ 和 $x\oplus e_i$ 不独立导致难以分析。而解决的办法,是利用 $\langle\cdot, \cdot\rangle$ 的线性性直接随机去猜 $\langle x, y\rangle$,调用 $\mathcal{A}$ 去算 $\langle x\oplus e_i, y\rangle$。
算法. 在输入 $f(y)$ 上:
- 令 $\ell = \lceil\log(2np^2(n) + 1)\rceil$,均匀随机采样 $s_1, …, s_\ell \leftarrow \mathrm{Uniform}(2^n)$。
- 随机猜 $t_i \leftarrow \{0, 1\}$;
- For $i = 1, 2, …, n$:
- $\qquad$For $\varnothing \subsetneq T \subseteq \{1, 2, …, \ell\}$:
- $\qquad\qquad$ $x_T \leftarrow \oplus_{j\in T} s_j$;
- $\qquad\qquad$ $\varphi_T \leftarrow \oplus_{j\in T} t_j$;
- $\qquad\qquad$ $\hat{y}_{i, T}\leftarrow \varphi_T \oplus \mathcal{A}(x_T\oplus e_i, f(y))$;
- $\qquad$ 猜 $y_i = \mathrm{Majority}(\hat{y}_i)$。
分析. $t_i$ 有 $1 / \mathrm{poly}(n)$ 的概率全猜对。若 $t_i$ 全猜对,只要 $\mathcal{A}(x_T\oplus e_i, f(y))$ 的中位数对,答案就对。而显然 $x_T$ 两两独立,由 Chebyshev Bound 可知 $\mathcal{A}(x_T\oplus e_i, f(y))$ 的中位数高概率对。
因此,我们得到了求 $f$ 的逆的、成功概率为 $\frac{1}{\mathrm{poly}(n)}$ 的算法,与 $f$ 是 OWF 矛盾。
Pseudorandomness
上一节已经证明了存在 OWF(OWP)便存在 OWF(OWP) w/ hardcore predicate。而这将直接导向 PRG:
定理 3.2.1. 若存在 OWP w/ hardcore predicate,则存在 $(n + 1)$-PRG。
证明. 设 $f$ 是一个带有 hardcore predicate $\mathsf{hc}$ 的 OWP。则
$$
\mathcal{G}(s) = f(s)\Vert \mathsf{hc}(s)
$$
是 PRG。注意因为 $f$ 是排列,有对于任意的 $\mathcal{D}$,
$$
\Pr_{r\leftarrow \mathrm{Uniform}(2^{n + 1})}[\mathcal{D}(r) = 1] = \Pr_{s\leftarrow \mathrm{Uniform}(2^n), b\leftarrow \mathrm{Uniform}(2)}[\mathcal{D}(f(s)\Vert b) = 1]
$$
后者和
$$
\Pr_{s\leftarrow \mathrm{Uniform}(2^n)}[\mathcal{D}(f(s)\Vert \mathsf{hc}(s))]
$$
必然差不多,不然能以不可忽略的概率优势猜对 $\mathsf{hc}$。
但凡能将随机种子拉长 1 位,便能拉长任意多项式位。这也是符合直觉的。
定理 3.2.2. 存在 $(n + 1)$-PRG 等价于存在 $\ell(n)$-PRG。
证明(Hybrid Argument). 存在 $\ell(n)$-PRG 蕴含存在 $(n + 1)$-PRG 显然——只需要截前 $n + 1$ 位即可。重点证明反向结论。
假设存在 $(n + 1)$-PRG $\mathcal{G}$,记 $\mathcal{G}(s) = \mathcal{G}_1(s)\Vert \mathcal{G}_2(s)$,其中 $|\mathcal{G}_1(s)| = 1$。构造 $\mathcal{G}’$ 为在输入 $s$ 上:
- $y_0 \leftarrow s$
- For $i = 1, 2, …, \ell(n) - n$:
- $\qquad$ $x_i \Vert y_i \leftarrow \mathcal{G}_1(y_{i - 1})\Vert \mathcal{G}_2(y_{i - 1})$;
- 输出 $x_1, …, x_{\ell(n) - n}, y_{\ell(n) - n}$。
假设存在 $\mathcal{G}’$ 的 p.p.t distinguisher $\mathcal{A}’$,构造如下的 $\mathcal{G}$ 的 p.p.t distinguisher $\mathcal{A}$:在输入 $t$ 上
- 随机 $i \leftarrow \mathrm{Uniform}(1, 2, …, \ell(n) - n + 1)$。
- 令 $y_0$ 为均匀随机数。
- For $j = 1, 2, …, \ell(n) - n$:
- $\qquad$ 若 $j < i$,令 $x_j\Vert y_j \leftarrow \$$;
- $\qquad$ 若 $j = i$,令 $x_j\Vert y_j \leftarrow t$;
- $\qquad$ 若 $j > i$,令 $x_j\Vert y_j \leftarrow \mathcal{G}_1(y_{j - 1})\Vert \mathcal{G}_2(y_{j - 1})$;
- 输出 $\mathcal{A}’(x_1, …, x_{\ell(n) - n}, y_{\ell(n) - n})$。
注意 $\Pr[\mathcal{A}(r) = 1 | i = \hat{i}] = \Pr[\mathcal{A}(\mathcal{G}(s)) = 1 | i = \hat{i} + 1]$,$i = \ell(n) - n + 1$ 将生成纯随机串,$i = 1$ 将模拟 $\mathcal{G}’$。因此
$$
\begin{aligned}
&\left|\Pr[\mathcal{A}(r) = 1] - \Pr[\mathcal{A}(\mathcal{G}(s)) = 1]\Pr\right| \\
&= \frac{1}{\ell(n) - n + 1}\left|\sum_{t = 1}^{\ell(n) - n + 1}\Pr[\mathcal{A}(r) = 1 | i = t] - \Pr[\mathcal{A}(\mathcal{G}(s)) = 1 | i = t]\right| \\
&= \frac{1}{\ell(n) - n + 1}\left|\Pr[\mathcal{A}(r) = 1 | i = 1] - \Pr[\mathcal{A}(\mathcal{G}(s)) | i = \ell(n) - n + 1]\right| \\
&= \frac{1}{\ell(n) - n + 1}\left|\Pr[\mathcal{A}’(r) = 1] - \Pr[\mathcal{A}’(\mathcal{G}’(s)) = 1]\right|
\end{aligned}
$$
不是不可忽略的。
有了 PRG,就可以构造 PRF。回忆在尝试 2.2.3,我们有一个串行地构造 PRF 的方法。该算法的问题是太慢,解决的办法是像线段树一样算函数值。
定理 3.2.3. 若存在 $2n$-PRG,则存在 $(n, n)$-PRF。
证明(Goldreich-Goldwasser-Micali Tree). 假设存在 $2n$-PRG $\mathcal{G}$,记 $\mathcal{G}(s) = \mathcal{G}_0(s)\Vert \mathcal{G}_1(s)$,其中 $\mathcal{G}_0(s) = \mathcal{G}_1(s) = n$。构造 $\mathcal{F}$:在密钥 $k$ 和输入 $x$ 下:
- 令 $u\leftarrow k$;
- For $i = 1, 2, …, n$:
- $\qquad$ $u\leftarrow \mathcal{G}_{x_i}(u)$;
- 输出 $u$。
证明是在查询走过的路上用 Hybrid Argument,这里省略。
定理 3.2.4. 若存在 $(2/3n, 2/3n)$-PRF,则存在 $n$-PRP。若存在 $(2n, 2n)$-PRF,则存在 $n$-强 PRP。
这个构造是所谓的 Feistel Network。
定义 3.2.2(Feistel Network). 设 $\mathcal{F}$ 是 PRF。如下的结构称作 $n$-Feistel Network($\Psi^n(\mathcal{F}_{k_1}, \mathcal{F}_{k_2}, …, \mathcal{F}_{k_n})$):设 $k = k_1\Vert k_2\Vert \cdots \Vert k_n$,在输入 $x = L_0 \Vert R_0$ 上:
- For $i = 1, 2, …, n$:
- $\qquad$ $L_i \leftarrow R_{i - 1}$;
- $\qquad$ $R_i \leftarrow L_{i - 1}\oplus \mathcal{F}(k_i, R_{i - 1})$;
- 输出 $L_n\Vert R_n$。
一个 Feistel Network 的输入记作 $[L, R]$,输出记作 $[S, T]$
下图来自 Introduction to Modern Cryptography。
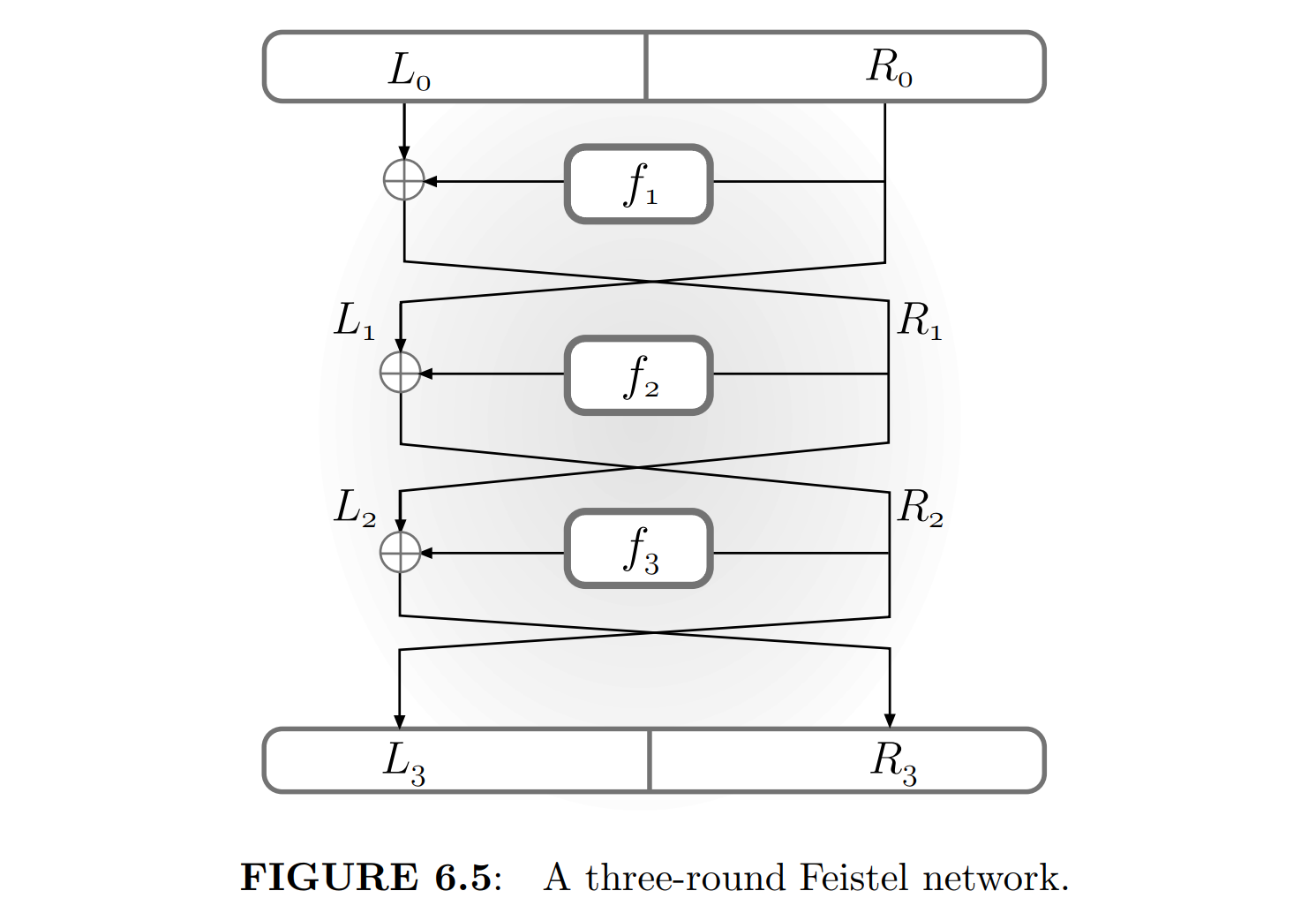
首先讨论一下怎么 Hack Feistel Network。这个套路是所谓的“字节反转攻击”,给输入异或上某个东西,然后观察输出的变化。
- $\Psi$ 不是 PRG. 注意总有 $S = R$;
- $\Psi^2$ 不是 PRP. 注意
$$
\Psi^2([L, R]) = [L \oplus f_1(R), R \oplus f_2(L \oplus f_1(R))]
$$
因此 $\Psi^2([L, R]) \oplus \Psi^2([L’, R]) = [L\oplus L’, …]$,可被区分。 - $\Psi^3$ 不是强 PRP. 注意
$$
\begin{aligned}
\Psi^3([L, R]) &= [R\oplus f_2(L\oplus f_1(R)), L \oplus f_1(R) \oplus f_3(R\oplus f_2(L\oplus f_1(R)))] \\
(\Psi^3)^{-1}([S, T]) &= [T \oplus f_3(S)\oplus f_1(S \oplus f_2(T \oplus f_3(S))), S \oplus f_2(T \oplus f_3(S))]
\end{aligned}
$$
那么考虑做两个正向询问 $[L, R]$ 和 $[L \oplus b, R]$ 得到 $[S, T]$ 和 $[S’, T’]$,你会发现有
$$
(\Phi^3)^{-1}(S, T’\oplus b) = […, R \oplus S \oplus S’]
$$
而正常排列高概率没有这种性质,因此 $\Psi^3$ 不是强 PRF。
然后来证明 Feistel Network 的安全性。
定理 3.2.5(Ruby-Lackoff). 若 $\mathcal{F}$ 是 PRF,则 $\Psi^3(\mathcal{F}_{k_1}, \mathcal{F}_{k_2}, \mathcal{F}_{k_3})$ 是 PRP。
证明(Sketch). 首先因为 $\mathcal{F}$ 是 PRF,可以用 Hybrid Argument 证明不可区分 $\Psi^3(\mathcal{F}_{k_1}, \mathcal{F}_{k_2}, \mathcal{F}_{k_3})$ 和 $\Psi^3(f_1, f_2, f_3)$(此处 $f_1, f_2, f_3$ 是三个真随机函数)。对于后者,高概率有 $R_1$ 两两不同,因此 $L_3 = R_2$ 和独立随机不可区分(自然也是两两不同),$R_3$ 和独立随机不可区分。这个证明是可以形式化的,具体参见附录。
定理 3.2.6(Ruby-Lackoff). 若 $\mathcal{F}$ 是 PRF,则 $\Psi^4(\mathcal{F}_{k_1}, \mathcal{F}_{k_2}, \mathcal{F}_{k_3}, \mathcal{F}_{k_4})$ 是强 PRP。
连 Sketch 都不想写了。
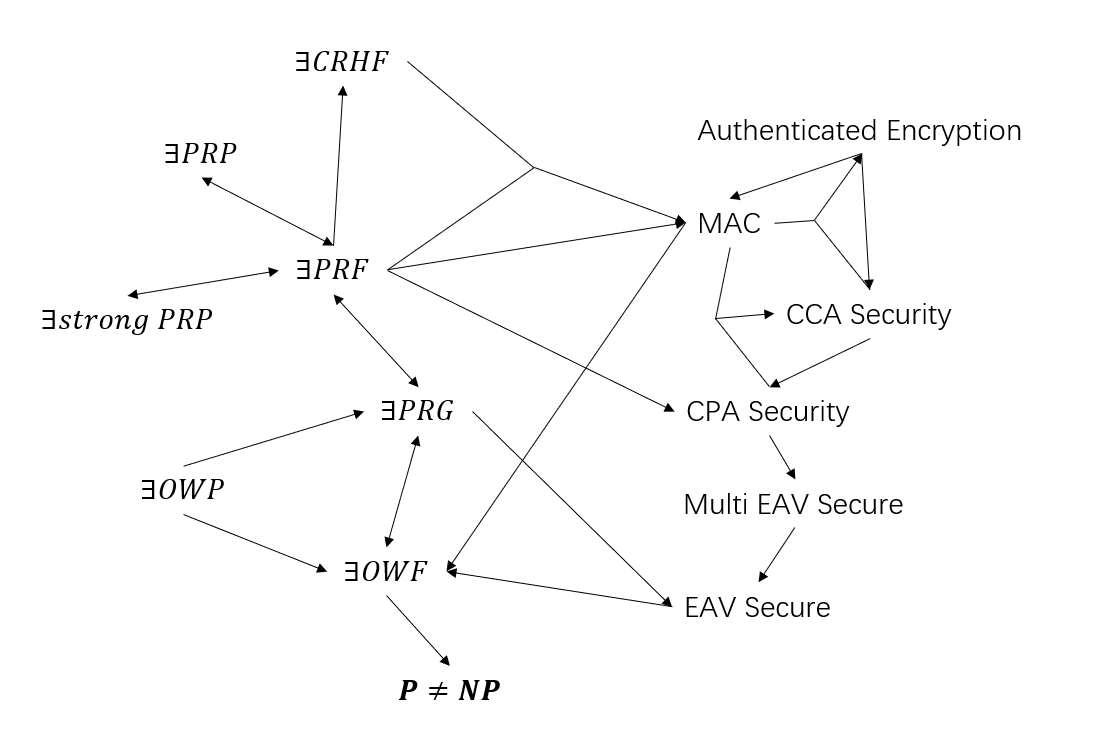
Appendix
Map of Reductions
H-Coefficient Technique
本节严格化 Ruby Lackoff 定理的证明,使用的技巧叫做 H-Coefficient 技巧。首先是一些记号。
- 记全体 $2^N\rightarrow 2^N$ 的函数为 $\mathscr{F}_N$;
- $G: K\rightarrow \mathscr{F}_N$ 称为函数构造子。其中 $K$ 是密钥集合。这里 $K$ 可以是:
- $(2^N)^k$:$k$ 个狭义上的密钥;
- $(\mathscr{F}_N)^k$:$f$ 个真随机函数,用于证明时将 PRF 替换为纯随机函数。
定义 4.2.1. 设 $q$ 是一个整数(i.e. 询问次数),$G$ 是一个函数构造子,$\{a_i\}_{1\leq i\leq q}$ 是 $\{0, 1\}^N$ 中一列互不相同的数,$\{b_i\}$ 是 $\{0, 1\}^N$ 中一列数。定义 $H(\boldsymbol{a}, \boldsymbol{b})$,或简明地记作 $H$,为使得 $G$ 把 $\boldsymbol{a}$ 映到 $\boldsymbol{b}$ 的密钥集合大小,即
$$
H(\boldsymbol{a}, \boldsymbol{b}) = |\{(f_1, …, f_r) : \forall 1\leq i\leq q, G(f_1, …, f_r)(a_i) = b_i\}|
$$
这个量刻画了排列的随即程度。直觉上,纯随机函数的 $H$ 都是一样大的($|\mathscr{F}_N| / 2^{Nq}$)。如果你有一个 $H$ 差的特别多(不可忽略概率),那么直接问对应的 $\boldsymbol{a}$,就可以产生不可忽略的 advantage。
定理 4.2.1(H-Coefficient Technique for CPA). 设 $\alpha, \beta$ 为两个正实数。$E$ 是 $\{0, 1\}^{Nq}$ 的一个子集,满足 $|E| > (1-\beta)\cdot 2^{Nq}$。
若:对于任意长度为 $q$ 的序列 $a_i$(两两不同),和长度为 $q$ 的序列 $b_i$($b_i\in E$),都有
$$
H(\boldsymbol{a}, \boldsymbol{b})\geq \frac{|K|}{2^{Nq}}(1 - \alpha)
$$
则:对于任意进行 $q$ 次询问的 p.p.t adversary $\mathcal{A}$,都有
$$
\left|\Pr_{f_1, …, f_r\sim \mathscr{F}_N} \left[\mathcal{A}^{G(f_1, …, f_r)}(1^N) = 1\right] - \Pr_{f\sim \mathscr{F}_N}\left[\mathcal{A}^f(1^N) = 1\right]\right| \leq \alpha + \beta
$$
证明. 注意,因为我们讨论的攻击都是 $\mathbf{P}/\mathrm{poly}$ 的,所以完全没有必要采用 p.p.t 的电路族,而是可以把最好的随机种子焊在电路里。对于一个确定性的 distinguisher $\mathcal{D}$,定义
$$
P^* = \frac{|f \in \mathscr{F}_N : \mathcal{D}^f(1^N) = 1|}{|\mathscr{F}_N|}, P = \frac{|\{(f_1, …, f_r)\in K : \mathcal{D}^{G(f_1, …, f_r)} = 1\}|}{|K|}
$$
欲证结论无非是 $|P^* - P|\leq \alpha + \beta$。这样一来,$P^*$ 的计算无需多言:$\mathcal{D}$ 既然是一个 oracle machine,那么抛开 oracle 访问就完全是一个正常的函数,假设其 oracle 纸带上的输入为 $\sigma_1, …, \sigma_q$,对应 $\mathcal{D}$ 对 $C_1, …, C_n$ 做了 oracle 访问(因为 $\mathcal{D}$ 是确定性算法,这两个序列是一一对应的)。设
$$
\mathscr{N} = |\{(\sigma_1, …, \sigma_q) \in \{0, 1\}^{Nq} : \mathcal{D}(\sigma_1, …, \sigma_q) = 1\}|
$$
则 $P^* = \frac{\mathcal{N}}{2^{Nq}}$。$P$ 的下界也是好算的。我们仅计算 $\in E$ 的 $(\sigma_1, …, \sigma_q)$,有
$$
\begin{aligned}
P&= \frac{1}{|\mathscr{K}|}\sum_{(\sigma_1, …, \sigma_n)\in \{0, 1\}^{Nq}} \mathbf{1}[\mathcal{D}(\sigma_1, …, \sigma_q) = 1 {\color{red}\wedge (\sigma_1, …, \sigma_q)\in E}]\cdot H(\boldsymbol{C}, \boldsymbol{\sigma}) \\
&\geq \frac{(\mathscr{N} - \beta \cdot 2^{Nq})\cdot \frac{|K|}{2^{Nq}}(1 - \alpha)}{|K|} \\
&\geq (P^* - \beta)(1 - \alpha) \geq P^* - \alpha - \beta
\end{aligned}
$$
注意这个算法跟 $\mathscr{N}$ 是什么完全没有关系。因此如果我定义
$$
\mathscr{N} = |\{(\sigma_1, …, \sigma_q) \in \{0, 1\}^{Nq} : \mathcal{D}(\sigma_1, …, \sigma_q) = 0\}|
$$
便对称地得到 $P \leq P^* + \alpha + \beta$。
现在,我们算 $\Psi^3$ 的 H-Coefficient。设算法问了 $q$ 次 $(L_0^i, R_0^i)$,得到结果为 $(L_3^i, R_3^i)$。我们来逐条翻译 Proof Scketch:
$R_1$ 高概率两两不同. 只需要计算使得存在 $i\ne j, R_1^i = R_1^j$ 的 $f_1$ 数量。注意 $R_1 = L_0 \oplus f(R_0)$。因此固定 $i, j$,分类讨论:
- 若 $R_0^i = R_0^j$,因为你必须问不同的位置,所以必须有 $L_0^i\ne L_0^j$,进而有 $R_1^i\ne R_1^j$;
- 否则,有 $f_1(R_0^i) \oplus f_1(R_0^j) = L_0^i \oplus L_0^j$。这样的 $f_1$ 的个数仅有 $\frac{|\mathscr{F}_N|}{2^N}$。
因此,至少有这么多的 $f_1$ 使得 $R_0$ 两两不同。
$$
|\mathscr{F}_n|\left(1 - \frac{q(q - 1)}{2^{N + 1}}\right)
$$
$R_2$ 近乎完全随机. 对于任意的输入,只要 $R_1$ 均两两不同,使得输出为 $R_2^1, …, R_2^q$ 为某个特定序列的 $f_2$ 数量就是 $\frac{|\mathscr{F}_n|}{2^{Nq}}$。
$R_3$ 近乎完全随机. 对于任意的输入,只要 $R_2$ 均两两不同,使得输出为 $R_3^1, …, R_3^q$ 为某个特定序列的 $f_3$ 数量同上。
然而,这里 $R_2$ 均两两不同就很难讨论了。不过我们特别引入了一个参数 $\beta$。于是可以取 $E$ 集合为 $L_3^i \ne L_3^j$ 的集合,这个集合的大小满足
$$
|E| \geq 2^{Nq}\cdot \left(1 - \frac{q(q - 1)}{2^{N + 1}}\right) \quad \Rightarrow \quad \beta = \frac{q(q - 1)}{2^{N + 1}} \
$$
上面的推导表明对于任意的 $(\boldsymbol{L}_i, \boldsymbol{R}_0)$ 和 $(\boldsymbol{L}_3, \boldsymbol{R}_3)\in E$ 都有
$$
H \geq \frac{|\mathscr{F}^N|^3}{2^{2Nq}}\left(1 - \frac{q(q - 1)}{2^{N + 1}}\right) \quad \Rightarrow \quad \alpha = \frac{q(q - 1)}{2^{N + 1}}
$$
结合定理 4.2.1,$\Psi^3$ 确实是 PRP。
注意这个 $H$ 还是一个非常对称的东西。因此定理 4.2.1 的证明几乎可以直接拓展到 CCA 上面,得到
定理 4.2.2. 设 $\alpha$ 是正实数。若
$$
H(\boldsymbol{a}, \boldsymbol{b})\geq \frac{|K|}{2^{Nq}}(1 - \alpha)
$$
则:对于任意进行 $q$ 次询问的 p.p.t adversary $\mathcal{A}$,都有
$$
\left|\Pr_{f_1, …, f_r\sim \mathscr{F}_N} \left[\mathcal{A}^{G(f_1, …, f_r), G^{-1}(f_1, …, f_r)}(1^N) = 1\right] - \Pr_{p\sim \mathscr{P}_N}\left[\mathcal{A}^{p, p^{-1}}(1^N) = 1\right]\right| \leq \alpha + \frac{q(q - 1)}{2^{N + 1}}
$$
补充的那一项是随机函数和随机排列的差异。