Revision | 计算理论导论
Abstract. 主干参考教学课件,预计将覆盖 Michael Sipser Book 的重要内容,以及 Arora Book 第一部分前八个章节的内容。
最后一节 交互式证明 写的非常糟糕。
形式语言和自动机
所谓语言者,无非是合法字符串的集合。或形式化地,一个字符集 $\Sigma$ 上的语言 $L$ 即是全体该字符集上正整数长度的字符串的一个子集,即 $L \subseteq \Sigma^*$。欲进行计算,换言之想要机械地识别一个语言 $L$,即需设计一个“机器” $M$,以一个字符串 $s$ 为输入,输出 accept 或者 reject,表示 $s\in L$ 或者 $s\notin L$。
自动机乃是一类最为简单的“机器”。作为对计算理论的初探,我们探究此类机器的能力边界所在。
有限状态自动机和正则语言
本节中,我们假设读者对自动机的工作方式有基本的直觉,且经受过一定的训练以能够设计简单的自动机。下文中的形式定义仅为完整性起见给出。
定义 1.1.1(确定性有限状态自动机 / DFA). 一个确定性有限状态自动机包含如下资料 $M = (Q, \Sigma, \delta, q_0, F)$,其中
- $Q$ 表示状态集合。
- $\Sigma$ 表示输入字符集合。
- $\delta: Q\times \Sigma\rightarrow Q$ 表示转移函数。
- $q_0$ 表示起始状态。
- $F\subseteq Q$ 表示接受状态集。
称确定性有限状态自动机 $M$ 接受(长度为 $n$ 的)字符串 $s$ 当且仅当存在一列状态 $r_0, r_1, …, r_n$ 满足 $r_0 = q_0$,$\forall i = 0, 1, …, n - 1$ 都有 $\delta(r_i, s_{i + 1}) = r_{i + 1}$ 且 $r_n \in F$。
称如下集合为 $M$ 识别的语言:$L(M) := \{w \in \Sigma^* : \text{$M$ accepts $w$}\}$。
定义中使用的字眼“确定性”,即是在描述此类自动机具有的特性:处于某状态时读入一个新字符,只能转移到某一个固定的状态。因此,最直接的对此类自动机性能拓展的尝试就是引入“非确定性”。
定义 1.1.2(非确定性有限状态自动机 / NFA). 一个非确定性有限状态自动机包含如下资料 $M = (Q, \Sigma, \delta, Q_0, F)$,其中
- $Q$ 表示状态集合。
- $\Sigma$ 表示输入字符集合。
- $\delta: Q\times (\Sigma \cup \{\varepsilon\}) \rightarrow \mathcal{P}(Q)$ 表示转移函数。这里 $\mathcal{P}(\cdot)$ 表示幂集,$\varepsilon$ 表示“空字符”,在判断两字符串是否相等时我们将忽略其中所有空字符。
- $Q_0$ 表示起始状态的集合。
- $F\subseteq Q$ 表示接受状态集。
称非确定性有限状态自动机 $M$ 接受(长度为 $n$ 的)字符串 $s$ 当且仅当存在字符串 $w := w_1w_2…w_m$,其中 $w_i\in \Sigma\cup\{\varepsilon\}$ 且 $w = s$,以及状态序列 $r_0, r_1, …, r_m$ 满足 $r_0\in Q_0$,对于任意的 $i = 0, 1, …, m - 1$ 都有 $r_{i + 1}\in \delta(r_i, w_{i + 1})$,且 $r_m\in F$。
然而可以发现这样的尝试是徒劳的。
定理 1.1.1. 对于一个语言 $A\in \Sigma^*$,存在一个 DFA $M$ 使得 $L(M) = A$ 当且仅当存在一个 NFA $M’$ 使得 $L(M’) = A$。
证明. 必要性显然,因为 DFA 可以自然地嵌入 NFA 中。为证明充分性,只需在 NFA $M’$ 的基础上构造一个状态集为 $\mathcal{P}(Q)$ 的 DFA(直觉上理解做当前能走到的全体状态)即可。$\blacksquare$
由是,DFA 和 NFA 具有相同的计算能力边界,因此将其统称做有限状态自动机。能被有限状态自动机识别的语言,称为正则语言,以 $\mathbf{REG}$ 指代全体正则语言构成的集合。可以发现,正则语言在某些操作下具有封闭性:
定理 1.1.2. 若 $A, B$ 是正则语言(分别被 NFA $M_1, M_2$ 识别),则以下语言都是正则语言:
- $A\cup B$、$A\cap B$ 和 $A^c$;
- $AB := \{ab : a\in A, b\in B\}$;
- $A^* := \cup_{n=1}^\infty A^n$。
证明. 利用 $M_1, M_2$ 构造对应的自动机即可。无非是一些构造两自动机的“乘积”、“串联”,或者从接收状态向起始状态连 $\varepsilon$ 边之类。$\blacksquare$
可凭这些操作构建计算机从业者熟知的“正则表达式”。
定义 1.1.3(正则表达式). 正则表达式 $\mathcal{R}$ 系指最小的满足如下条件的集合:
- 对于任意的 $a\in \Sigma$,$a\in \mathcal{R}$;$\varnothing \in \mathcal{R}$;$\varepsilon \in \mathcal{R}$。
- 若 $R_1, R_2\in \mathcal{R}$,则 $R_1\cup R_2, R_1\cap R_2, R_1^c, R_1R_2, R_1^*\in \mathcal{R}$。
可以结合以上论述,望文生义地定义何为“一个正则表达式描述的语言”,节约篇幅此处不写。
直觉上便有
定理 1.1.3. 一个语言是正则语言当且仅当存在一个正则表达式描述之。
证明. 必要性. 显然,因为正则表达式中的基本元素(1)都是正则语言,且正则语言对于(2) 中的操作都封闭。
充分性. 现有正则语言 $L$,其能被一个 NFA $M$ 识别。不失一般性可设 $M$ 的起始节点和接受节点唯一,且没有 $\varepsilon$ 边(读者自行思考如何改造其余形式的 NFA)。
方便起见,我们另外定义一种非确定性有限状态自动机。其每条转移边上都是一个正则表达式,能够从此转移当且仅当字符串的一个前缀能够匹配上此正则表达式。容易证明,这种自动机的能力和 NFA 相同。可交替进行如下两种操作,将 $M$ 逐步改造做一个只有起始节点和接受节点的、只有一条连接它们的边的自动机:
去重边. 若存在两个状态 $u, v$,从 $u$ 到 $v$ 有 $k > 1$ 条转移边,边上的正则表达式依次是 $r_1, …, r_k$。则将其一并删去,并加一条标注 $r_1 \cup \cdots \cup r_k$ 的转移边,得到的自动机识别的语言不变。
删点. 选择一个非起始非中止节点 $p$。删去它和与之相关的所有边,然后连接
$$
\{(u, v, r_1r_2) : \text{transition $(u, p, r_1)$ and $(p, v, r_2)$ exists}\}
$$
最后得到的自动机唯一的转移边上缩写之正则表达式即为描述该 NFA 识别的语言的正则表达式。$\blacksquare$
然而很遗憾,正则语言不是全部的语言。即 $\mathbf{REG} \subsetneq \mathcal{P}(\Sigma^*)$。比如考虑语言 $\{0^n1^n : n\in \mathcal{N}\}$,任何尝试以正则表达式或自动机识别之的尝试都是徒劳无功的。这是因为直觉上,输入一个长度大于有限状态自动机状态数的字符串,必然会走出一个环,而重复走这个环,不会对接受 / 拒绝的决策造成任何影响。此直觉表明正则语言一定具有某种特殊的结构。形式化地,有
定理 1.1.4(泵引理). 对于任意的 $L\in \mathbf{REG}$,都存在一个常数 $p$ 使得:对于任意的 $s\in L, |s| \geq p$,都可将 $s$ 划分做三段(即 $s = xyz$)使得
- $|y| > 0, |xy| < p$;
- 对于任意的 $i\in \mathbb{N}$,都有 $xy^iz\in L$。
证明. 设 $L$ 被一个 DFA $M$ 识别,其状态集为 $Q$。这里 $p$ 无非是 $|Q| + 1$。则根据鸽巢原理 $s$ 在 $M$ 上行走的一个路径必然形如一个“$\rho$”加上一段后续的过程。将 $x$ 取作“$\rho$”上进入环时读入的字符串,$y$ 取作环上的字符串,$z$ 取作后续字符串,这就是一个满足条件的切片。$\blacksquare$
另外一条刻画正则语言的结构的定理如下,该定理对于自动机的最小化也有一些帮助:
定理 1.1.5(Myhill–Nerode). 对于语言 $L$,定义等价关系
$$
\sim_L := \{(x, y) \in \Sigma^*\times \Sigma^* : \forall w\in \Sigma^*, \text{$M$ accepts $xw$ iff $M$ accepts $yw$}\}
$$
则 $L$ 是正则语言当且仅当 $|\Sigma^* / \sim_L| < \omega$($\omega$ 是 $\mathbb{N}$ 的基数)。
证明. 若在一个 DFA 上,两个字符串输入后转移到了同一个节点,那么他们等价。因此对于正则语言 $L$ 必有 $|\Sigma^* / \sim_L| \leq |Q|$。同样,可尝试构造一个 $Q = \Sigma^* / \sim_L$ 的 DFA。因为若 $x\sim_L y$ 则对于任意的 $c\in \Sigma$ 都有 $xc\sim_L yc$,所以它必是良定义的。$\blacksquare$
(非确定性)下推自动机和上下文无关语言
一个增强自动机能力的尝试是给它增加“内存”。比如有限状态自动机在识别上方的 $01$ 语言时遇到的困难,只要有一个栈便可迎刃而解。
本节探究这种附带一个栈的自动机的计算能力。
定义 1(非确定性下推自动机 / NPDA). 一个非确定性下推自动机包含一下资料:$(Q, \Sigma, \Gamma, \delta, q_0, F)$,其中
- $Q$ 是状态集;
- $\Sigma$ 是输入字符集;
- $\Gamma$ 是栈字符集;
- $\delta : Q\times (\Sigma \cup \{\varepsilon\})\times (\Gamma \cup \varepsilon) \rightarrow \mathcal{P}(Q\times \Gamma_{varepsilon})$ 为转移函数;
- $q_0\in Q$ 为起始状态;
- $F\subseteq Q$ 为接受状态集合。
一个 NPDA $M$ 接受一个字符串 $s$ 若存在字符串 $w = w_1w_2…w_m$、一列字符串 $t_0, t_1, …, t_m$、一列状态 $r_0, r_1, …, r_m$,满足:
- $w = s$,$r_0 = \varepsilon$,$r_0 = q_0$;
- 对于任意的 $i = 0, 1, …, m - 1$ 都有存在 $a, b\in \Gamma$ 和 $s\in \Gamma^*$,满足 $t_i = sa, t_{i + 1} = sb$,且 $(q_{i + 1}, b)\in \delta(q_i, w_{i + 1}, a)$。
方便起见,以后若 $(v, b)\in \delta(u, c, a)$,我们将称存在转移边 $(u\xrightarrow{c, a, b} v)$。
因为此类自动机带上了一个副作用(栈),所以不好直接使用上一节中的手法来探究 NPDA 识别的语言的边界(甚至不能知道定理 1.1.2 中的结论是否成立)。我们需要转换视角。
此处引入了栈,所以这种自动机将能够做括号匹配一类的工作。这让我们联想到用递归的语法规则定义的语言——上下文无关语言。这个上下文无关语言就是软件科学和编译原理中常见的那个上下文无关语言,因此我们仍然假设读者有相关直觉,以下形式定义仅是为完整性起见给出。
定义 1.2.2(上下文无关文法 / CFG). 一个上下文无关文法 $G$ 包含以下资料:$(V, v_0, \Sigma, R)$ 其中
- $V$ 为变量集。
- $v_0\in V$ 为起始变量。
- $\Sigma$ 为终止符集。一般认为 $V\cap \Sigma = \varnothing$。
- $R\in \mathcal{P}(V\times (V\cup \Sigma)^*)$ 是替换规则(有限集)。这个看起来很抽象的类型表示 $R$ 中的元素形如 $s \rightarrow t$,其中 $s\in V, t\in (V\cup \Sigma)^*$。
对于 $s, t\in (V\cup \Sigma)^*$,称 $s\Rightarrow t$ 当且仅当可以用 $R$ 中的替换规则 $a\rightarrow$,将 $s$ 中的一个变量 $a$ 替换为 $b$ 得到 $t$。若 $s$ 能够经有限次替换得到 $t$,记 $s\Rightarrow^* t$。$G$ 生成的语言定义做 $L(G) := \{t : v_0\Rightarrow^* t\}$。
生成一个字符串的过程可以用一棵树刻画,这棵树称作语法树。
能被某个上下文无关文法生成的语言称为上下文无关语言,其全体构成集合 $\mathbf{CFL}$。
定理 1.2.1. 对于语言 $L$,$L\in \mathbf{CFL}$ 当且仅当存在 NPDA $M$ 使得 $L(M) = L$。
证明. 必要性. 对着替换规则写一个 NPDA 即可。显然,栈中存当前可能替换出已经读入部分的字符串的中间结果即可(每次识别栈顶连续若干个元素是否是某个替换规则的产物,若是将其全部弹出并压入该替换规则的变量)。
充分性. 不失一般性可设该 NPDA $M$ 只有一个接受节点 $f$,转移时要么压栈、要么弹栈,接受任意一个字符串时栈都可以是空的(改造方式留予读者)。则可以用如下的上下文无关文法刻画 NPDA 识别一个字符串过程中的行走路径及栈的运动:
- 变量集为 $Q\times Q$,每个元素 $(u, v)$ 表示存在一条路径从 $u$ 走到 $v$,且保持行走过程中栈不低于初始未知,结束时栈恰为原来的栈。
- 起始变量为 $(q_0, f, \varepsilon)$。
- 终止符集为 $\Sigma$。
- 若存在转移边 $u\xrightarrow{c_1, \varepsilon, b} p_1$ 和转移边 $p_2\xrightarrow{c_2, a, \varepsilon} v$,则添加替换规则 $(u, v) \rightarrow c_1(p_1, p_2)c_2$;对于任意三个状态 $q_1, q_2, q_3\in Q$,添加替换规则 $(q_1, q_3)\rightarrow (q_1, q_2)(q_2, q_3)$。
于是便得到了一个生成 $M$ 所识别语言的 CFG,因此 $L(M)\in \mathbf{CFL}$。$\blacksquare$
推论 1.2.2. $\mathbf{REG}\subsetneq \mathbf{CFL}$。
至此,我们完全将非确定性下推自动机和上下文无关语言联系起来。然后便能探究其能力边界。
定理 1.2.3(泵引理). 对于任意的 $A\in \mathbf{CFL}$,都存在常数 $p$ 使得对于任意的 $s\in \Sigma^*$,若 $|s| > p$,则 $s$ 可被切成五段 $s = uvxyz$,满足:
- $|vy| > 0$;
- $|vxy| < p$;
- 对于任意的 $i\in \mathbb{N}$,都有 $uv^ixy^iz\in A$。
证明. 设 $A = L(G)$,其中 $G$ 是一个上下文无关文法。取 $p = (|V| + 1)^{r_m + 1}$,其中 $r_m = \max\{|v| : (u\rightarrow v) \in R\}|$。这个 $p$ 使得生成长度大于 $p$ 的语法树深度必超过 $|V|$,进而生成过程中存在一个变量在一条竖直的链上出现了两次。下图道尽一切:
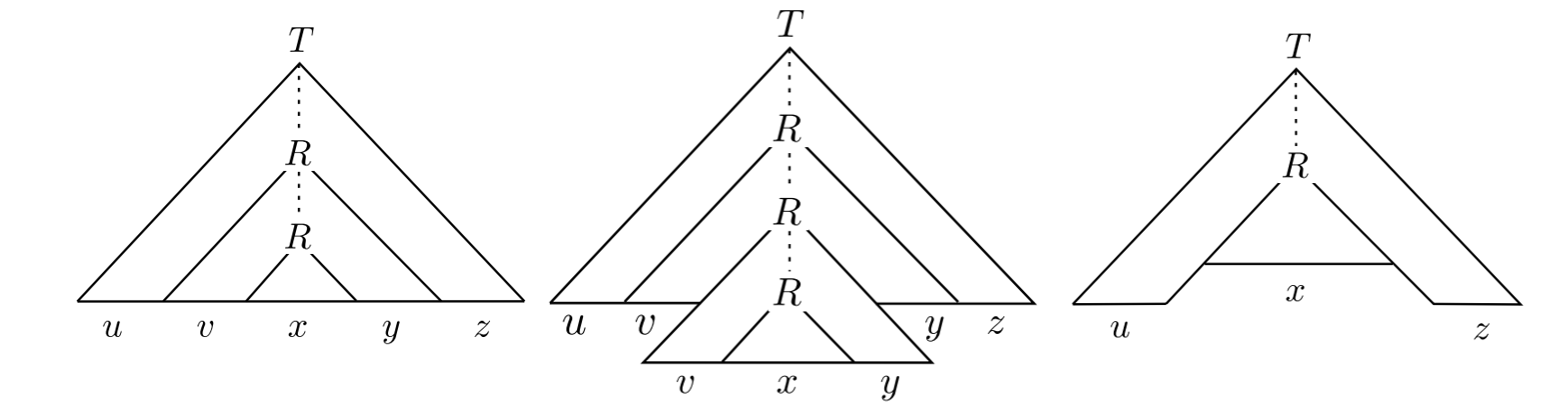
得证。$\blacksquare$
因此,我们可以说明 $L_1 = \{0^n1^n0^n : n\in \mathbb{N}\}$ 这类语言是上下文无关语言。因此 $\mathbf{CFL}\subsetneq \mathcal{P}(\Sigma^*)$。
观察到令 $L_2 = \{0^n1^n1^m : n, m\in \mathbb{N}\}, L_3 = \{0^n1^m0^m : n, m\in \mathbb{N}\}$,有 $L_1 = L_2 \cap L_3$。因此 $\mathbf{CFL}$ 对交不封闭。但是可以证明 $\mathbf{CFL}$ 对上下文无关语言和正则语言的交封闭(只需要改造自动机部分,和存储无关)、对并封闭。进而,通过证明 $\overline{L_1}\in \mathbf{CFL}$,可以证明 $\mathbf{CFL}$ 对补不封闭。
可计算性理论
再尝试拓展自动机的计算能力边界。我们将赋予其完全的访存能力,得到图灵机。这将是(就目前已知)物理上能够实现的最强的计算模型。但是很遗憾,图灵机能够“识别”的语言仍只是全部语言的真子集。
图灵机的基本定义
定义 2.1.1(确定性图灵机 / DTM). 一个 $k$ 带图灵机包含如下资料:七元组 $(Q, \Sigma, \Gamma, \delta, q_0, q_{acc}, q_{rej})$,其中
- $Q$ 为状态集,$q_0\in Q$ 为起始状态,$q_{acc}, q_{rej}\in Q$ 分别为(停机并)接收状态和拒绝状态。
- $\Sigma$ 为输入字符集,$\Gamma$ 为纸带字符集。
- $\delta: Q\times \Gamma^k\rightarrow Q\times \Gamma^k\times \{L, S, R\}^k$ 为转移函数,描述在某状态下每个纸带的读写头读入到某些字符将转移到何状态、写何字符、向何处移动读写头。
你可以将其想象成一个配备了 $k$ 条无限长的纸带的抽象的机器。
通常 $\Gamma$ 中有两个特殊字符:$\triangleright$ 和 $\text{_}$,表示纸带开头和空格。
定义 2.1.2(格局). 图灵机的一个格局描述了某一时刻图灵机和纸带的情况,它是一个包含如下资料的元组 $(q, t_1, …, t_k, h_1, …, h_k):
- $q$ 表示当前状态;
- $t_1, …, t_k$ 表示当前纸带内容(仅包含最后一个非 $\text{_}$ 前的内容);
- $h_1, …, h_k$ 表示当前读写头位置。
图灵机的计算过程,在此我们不进行琐碎的形式定义。只明确以下几点:
- 图灵机的面临的初始情况由初始格局 $C_0$描述。此时图灵机处于状态 $q_0$,$k$ 条纸带内容为
$$
\begin{aligned}
\text{tape $1$}\quad & \boxed{\triangleright \texttt{ s } \text{_ _ _} \cdots} \\
\text{tape $2$}\quad & \boxed{\triangleright \text{_ _ _} \cdots} \\
\vdots\quad & \\
\text{tape $k$}\quad & \boxed{\triangleright \text{_ _ _} \cdots} \\
\end{aligned}
$$
其中 $\texttt{s}$ 为输入。 - 图灵机从 $k$ 条纸带读入字符,执行 $\delta$ 要求的转移。
- 如果运行到 $q_{acc}$(或者 $q_{rej}$),停机并接受(或者拒绝)。
由此,一个图灵机 $M$ 识别(recognize)的语言为 $L(M) := \{s : \text{$M$ halts and accepts $s$}\}$。注意,图灵机可能有环,因此在某些输入上可能不停机,此类语言即使能被图灵机识别,可能也没有现实意义,因此你不知一个有环的图灵机在某输入上将何时停机,任何截断其运行的操作都将是武断的。可以被图灵机识别的语言称为图灵可识别的,或者在递归论的术语下称作递归可枚举的,其全体构成集合 $\textbf{RE}$。
自然,容易想到图灵机识别语言的另一种模式,即其在所有不属于该语言的输入上停机并拒绝。我不知道这类语言的中文名,但是其全体构成集合 $\mathbf{coRE}$。
如果一个图灵机 $M$ 在一切输入上都停机,那么它被称为一个判定机(decider),且称 $M$ 判定(decides) $L(M)$。若一个语言能被一个判定机判定,则称其为图灵可判定的,或者在递归论的术语下称作递归的,其全体构成集合 $\mathbf{R}$。
补充一些关于图灵机的信息:
- 函数计算. 不只是简单接受和拒绝(只是计算函数 $f : \{0, 1\}^* \rightarrow \{0, 1\}$)。称 $M$ 计算 $f : \{0, 1\}^* \rightarrow \{0, 1\}^*$,若其在任意输入 $x$ 上都停机并在某一条输出纸带上写 $f(x)$。
- 运行时间. 称一个图灵机的运行时间为 $T(n)$,若它在任意输入 $x$ 上都将在 $T(|x|)$ 步内停机。称 $T$ 是 time-constructable 的,若存在一个图灵机在 $T(n)$ 时间内计算 $x\mapsto \lfloor T(|x|)\rfloor$。
图灵机可以有一些变种。比如图灵机可以有更多的纸带和更大的字符集,但是在识别语言的意义下,这些变种都和朴素的图灵机等同。因为
定理 2.1.1. 对于任意计算 $f : \{0, 1\}^* \rightarrow \{0, 1\}$ 的图灵机 $M$,其纸带字符集为 $\Gamma$,运行时间为 $T(n)$,则存在另一个图灵机 $M’$ 也计算 $f$,但其纸带字符集仅为 $\{0, 1, \triangleright, \text{_}\}$,时间为 $O(T(n)\log |\Gamma|)$。
证明. 编码字符集即可。$\blacksquare$
定理 2.1.2. 对于任意计算 $f : \{0, 1\}^* \rightarrow \{0, 1\}$ 的图灵机 $M$,其使用 $k$ 条纸带,运行时间为 $T(n)$,则存在另一个图灵机 $M’$ 也计算 $f$,但其只是用一条纸带,时间为 $O(kT^2(n))$。
证明. 将纸带穿插一下即可。可能需要维护一些必要的辅助信息,但是都是琐碎的。$\blacksquare$
同样,仅考虑可判定性,确定性图灵机和非确定性图灵机也是等价的。构造是琐碎的,此处不写。
接下来介绍可计算理论中的重要内容:通用图灵机。直觉上,我们希望一个机器能够运行各种算法(就如同现在的电脑)。这样的机器称作通用图灵机。
首先,因为图灵机涵盖的资料都是有限的,所以存在一个图灵机到 $\{0, 1\}^*$ 的双射,称作图灵机为编码。编号为 $\alpha$ 的图灵机记作 $M_\alpha$。
定理 2.1.3(通用图灵机). 存在一个图灵机 $U$,使得对于任意的 $x, \alpha\in \{0, 1\}^*, U(x, a) = M_\alpha(x)$。特别地,若 $M_\alpha$ 在 $x$ 上运行 $T$ 步边停机,则 $U$ 在 $CT\log T$ 步内停机,其中 $C$ 是只和 $M_\alpha$ 有关的常数。
Remark. 似乎 $CT\log T$ 是前沿结果,甚至还有 $\sqrt T$ 空间模拟的前沿结果,这里我们只会证 $CT^2$。
证明(Sketch). 这个图灵机将使用五条纸带,依次存放输入 $x$、$M$ 的描述(用编码算出)、运行中纸带的情况、$M$ 现在的状态、输出,必要时附带一条草稿纸。模拟时每步取对应状态和字符,然后查表得知转移函数,最后将变化写回。简单思考发现这些事情都是可以在 $O(T)$ 内实现的。$\blacksquare$
关于可计算性的一些论题
首先,我们罗列一些可计算的语言。在此处,我们将使用一些所谓的“算法”来描述图灵机,这样做的根据是 Turing-Church Thesis。并且,方便起见,我们将混淆机器(包括自动机和图灵机)的编码和机器本身。
一些平凡的断言. 有以下显然的包含关系:
- $\mathbf{REG}\subset \mathbf{R}$;
- $\mathbf{CFG}\subset \mathbf{R}$。
这是因为有限状态自动机和 PDA 可以嵌入必然停机的图灵机之中。
关于自动机的可判定语言. 以下几个语言都是可判定的:
- $\mathrm{A_{DFA}} := \{ \langle A, w\rangle : \text{$A$ is a DFA and $A$ accepts $w$} \}$;
- $\mathrm{E_{DFA}} := \{ A : \text{$A$ is a DFA and $L(A) = \varnothing$} \}$;
- $\mathrm{EQ_{DFA}} := \{ \langle A, B\rangle : \text{$A, B$ are DFAs and $L(A) = L(B)$} \}$;
- $\mathrm{A_{CFG}} := \{ \langle G, w\rangle : \text{$G$ is a CFG and $G$ generates $w$} \}$;
- $\mathrm{E_{CFG}} := \{ \langle G\rangle : \text{$G$ is a CFG and $L(G) = \varnothing$} \}$。
前三个命题换成 NFA、正则表达式也成立,因为存在 NFA / 正则表达式转 DFA 的算法。
欲证明这些断言,只需设计一些算法。这些算法无非是一些在自动机 / CFG 上面进行深度优先搜索之类的操作。
值得注意的是,用证明 $3$ 的手法(你可能会想构造一个识别 $A\oplus B$ 的自动机,这里 $\oplus$ 表示对称差)不能证明 $\mathrm{EQ_{CFG}}$ 是可判定的,因为 CFG 在对称差下不封闭。后续我们会论述 $\mathrm{EQ_{CFG}}$ 是不可判定的。
接下来我们论证不可判定语言的广泛存在性。
定理 2.2.1. 存在不可识别的语言。即 $\mathbf{RE}\subsetneq \mathcal{P}(\{0, 1\}^*)$。
证明. 为了证明真子集,只需要证明其不等势即可。显然存在 $\mathbf{RE}$ 到图灵机的单射,但是图灵机都有编码,因此可嵌入 $\mathbb{N}$。于是
$$
|\mathbf{RE}| \leq \mathbb{N} < 2^{|\mathbb{N}|} = |\mathcal{P}(\{0, 1\}^*)|
$$
确实不等势,因此是真子集。$\blacksquare$
定理 2.2.2. 若一个语言及其补都是可识别的,则它是可判定的,即 $\mathbf{R} = \mathbf{RE} \cap \mathbf{coRE}$。
证明. 同时交替运行识别该语言及其补的图灵机。对任意输入,总有一个将停机,因此该语言可判定。$\blacksquare$
$\mathbf{R}\ne \mathbf{RE}$ 的证明是一个经典的对角线法。
定理 2.2.3. 存在可识别但不可判定的语言,即 $\mathbf{R}\subsetneq \mathbf{RE}, \mathbf{R}\subsetneq \mathbf{coRE}$。
证明. 考虑如下语言 $\mathrm{UC}$:
$$
\mathrm{UC}(\alpha) := \begin{cases}
\text{reject} & \text{$M_\alpha(\alpha)$ halts and accepts.} \\
\text{accept} & \text{otherwise.}
\end{cases}
$$
假设存在一个图灵机 $M$ 能够判定此问题,其编码为 $\alpha$,则无论 $M(\alpha)$ 接受还是拒绝都将推出对方,导出矛盾。而显然 $\mathrm{UC}\in \mathbf{coRE}$,这证明了第二个断言。
另考虑如下语言(著名的停机问题) $\mathrm{HALT}(\langle \alpha, x\rangle) := \{\text{$M_\alpha$ halts on input $x$}\}$。显然 $\mathrm{HALT}\in \mathbf{RE}$,但如果 $\mathrm{HALT}\in \mathbf{R}$,则可以结合一个通用图灵机来判定 $\mathrm{UC}$,因此 $\mathrm{HALT}\notin \textbf{R}$,这证明了第一个断言。$\blacksquare$
注意,我们证明一个语言不可判定时,几乎必然使用以下两种方法之一:对角线法和规约。而在进行规约时,一般有两种惯用的手法:
- 调用子过程. 构造一个(可能使用 UTM 的)图灵机,它通过一些自己的步骤和模拟 $B$ 问题的判定机来判定问题 $A$。若 $A$ 是不可判定的,便导出矛盾,进而证明 $B$ 不可判定。
- Map Reduction. 这是上述方法的一个上层建筑。若存在可计算的函数 $f : \{0, 1\}^*\rightarrow \{0, 1\}^*$ 使得 $x\in A \Leftrightarrow f(x)\in B$,则称 $A \leq_m B$。容易证明,$A\leq_m B$,则 $A$ 不可判定蕴含 $B$ 不可判定、$B$ 可判定蕴含 $A$ 可判定。
以下是更多例子。
一些规约的应用. 以下语言都是不可判定的:
- $\mathrm{A_{TM}} := \{ \langle M, w\rangle : \text{$M$ is a TM and accepts $w$}\}$;
- $\mathrm{E_{TM}} := \{ M : L(M) = \varnothing \}$;
- $\mathrm{EQ_{TM}} := \{ \langle M_1, M_2\rangle : L(M_1) = L(M_2) \}$;
- $\mathrm{REGULAR_{TM}} := \{ M : L(M) \in \mathbf{REG} \}$;
容易发现 $\mathrm{UC} \leq_m \mathrm{A_{TM}}$,$\mathrm{E_{TM}} \leq \mathrm{EQ_{TM}}$。(断言 1、3 证毕)
因此着重证明第 2 条和第 4 条。现证明 $\mathrm{UC} \leq_m \mathrm{E_{TM}}$,考虑构造如下可计算函数 $f$:它将 $\alpha$ 映射到如下图灵机 $M’$ 的编码:
- 在输入 $x$ 上:
- 如果 $x\ne \alpha$,拒绝。
- 否则,模拟 $M_{\alpha}$ 在 $\alpha$ 上的运行并输出对应结果。
注意,这里只是要计算 $M’$ 的编码,无非是做一些程序填空的工作,因此 $f$ 是可计算的。而若 $\alpha \in \mathrm{UC}$,则 $M’ = M_{f(\alpha)}$ 将拒绝一切,否则 $M’$ 将接受 $\alpha$。因此,$\alpha\in \mathrm{UC} \Leftrightarrow f(\alpha) \in \mathrm{E_{TM}}$,得到 $\mathrm{UC} \leq_m \mathrm{E_{TM}}$。(断言 2 证毕)
接下来证明 $\mathrm{A_{TM}} \leq_m \mathrm{REGULAR_{TM}}$。设 $M_0$ 是判定语言 $\{0^n1^n : n\in \mathbb{N}\}$ 的图灵机。考虑构造如下可计算函数 $f$:他将 $\langle M, w\rangle$ 映射到如下图灵机 $M’$ 的编码:
- 在输入 $x$ 上:
- 模拟 $M$ 在 $w$ 上的运行。
- 若接受,则模拟 $M_0$ 在 $x$ 上的运行。
- 若拒绝,则拒绝。
那么,如果 $M$ 接受 $w$,则 $L(M’) = L(M_0)$,不是正则语言,否则 $L(M’) = \varnothing$。因此 $\langle M, w\rangle\in \mathrm{A_{TM}} \Leftrightarrow f(\langle M, w\rangle)\in \mathrm{REGULAR_{TM}}$,得到 $\mathrm{A_{TM}} \leq_m \mathrm{E_{TM}}$。(断言 4 证毕)
我们已经证明了如此之多的关于图灵机的性质的不可判定性。事实上,一切非平凡的关于图灵机的性质都是不可判定的。该定理的证明与上述断言 $4$ 如出一辙。
定理 2.2.4(Rice). $P$ 是一个关于图灵机的谓词。称 $P$ 是非平凡的,当且仅当 $\exists L_1, L_2\in \mathbf{RE}, P(L_1) \wedge \neg P(L_2)$。则对于任意的非平凡的 $P$,语言 $\mathrm{P_{TM}} := \{ M : P(M) \}$ 都是不可判定的。
证明. 不失一般性,设 $M_1$ 能识别 $L_1$,$L_2 = \varnothing$。(这是因为 $P(\varnothing)$ 或不然,若 $P(\varnothing)$ 我们可以先证明 $\overline{P_{TM}}$ 不可判定,然后用 $\mathbf{R} = \mathbf{RE} \cap \mathbf{coRE}$ 推出 $\overline{P_{TM}}$ 必然也不可判定)
接下来证明 $\mathrm{A_{TM}} \leq_m \mathrm{P_{TM}}$。为此构造函数 $f$,它将 $\langle M, w\rangle$ 映射到如下图灵机的编码:
- 在输入 $x$ 上:
- 模拟 $M$ 在 $w$ 上的运行。
- 若接受,模拟 $M_1$ 在 $x$ 上的运行;
- 否则,拒绝。
显然 $\langle M, w\rangle\in \mathrm{A_{TM}}\Leftrightarrow f(\langle M, w\rangle)\in \mathrm{P_{TM}}$。$\blacksquare$
最后介绍几个和 CFG 相关的不可判定性证明。这些证明主要依赖于图灵机的合法或非法格局序列可以被巧妙地表示出。
PCP Problem. 给定一个二元组的有限集 $(\Sigma^* \times \Sigma^*) \supseteq S := \{(a_1, b_1), …, (a_k, b_k)\}$。判断是否存在一列(可重复的)标号 $i_1, …, i_r$ 使得 $a_{i_1}…a_{i_r} = b_{i_1}…b_{i_r}$。
有 $\mathrm{PCP}\in \mathbf{RE}\setminus \mathbf{R}$。
设 $\mathrm{PCP}_{(a, b)}$ 表示固定开头为 $(a, b)$ 的 $\mathrm{PCP}$。显然 $\mathrm{PCP}_{(a, b)} \leq_m \mathrm{PCP}$。(需要一些简单的“错位”构造)
用如下形状的字符串来包囊一个单纸带图灵机的格局的全部信息:
$$
t_1 t_2\cdots t_{h - 1} \texttt{ [head: $q$] } t_h \texttt{ [/head] } t_{h + 1} \cdots t_{m}
$$
我们证明 $\mathrm{A_{TM}}\leq_m \mathrm{PCP}$。为此,针对 $M$ 和 $w$ 构造一个 PCP 问题的实例 $S$:
- 向 $S$ 中加入 $(a_0, b_0) := (\varepsilon, \texttt{ [head: $q_0$] } \triangleright \texttt{ [/head] } w)$,表示初始格局。
- 对于任意的 $c\in \Gamma$,向 $S$ 中加入 $(c, c)$。
- 对于任意的 $c_1, c_2\in \Gamma, q\in Q$,若 $\delta(q, c_2) = (q’, c_3, L)$,向 $S$ 中加入
$$
(c_1\texttt{ [head: $q$] } c_2 \texttt{ [/head] }, \texttt{ [head: $q’$] } c_1 \texttt{ [/head] } c_3)
$$
对于向右移动和不动的情况,做类似的构造。相信聪明的读者可以洞悉这个构造的奥妙。 - 对于任意的 $c\in \Gamma$,向 $S$ 中加入 $(c, \varepsilon)$,并向 $S$ 中加入 $(\texttt{ [head: $q_{acc}$] } c \texttt{ [/head] }, \varepsilon)$
容易看出 $S$ 的解对应一个合法的接受 $w$ 的格局序列。因此 $S$ 有解当且仅当 $M$ 接受 $w$,即 $\mathrm{A_{TM}}\leq \mathrm{PCP}_{(a_0, b_0)}$。$\blacksquare$
其他关于 CFG 的不可判定问题. 以下问题不可判定。
- $\mathrm{AMB_{CFG}}$ 判断一个 CFG 是否是无歧义的;
- $\mathrm{ALL_{CFG}}$ 判断一个 CFG 是否生成一切;
- $\mathrm{EQ_{CFG}}$ 判断两个 CFG 的语言是否相同。
节约篇幅,不予详细证明。
- 证明 $\mathrm{PCP}\leq_m \mathrm{AMB_{CFG}}$。
- 设计 NPDA 来识别一切非法的格局序列,进而证明 $\mathrm{A_{TM}} \leq_m \mathrm{ALL_{CFG}}$。
- 因为存在生成一切的 CFG,所以显然 $\mathrm{ALL_{CFG}}\leq_m \mathrm{EQ_{CFG}}$。
复杂度理论
现实中除了考虑问题是否可判定外,还需要度量其需要的资源。
时间复杂度
定义 3.1.1(确定性时间复杂度类). $T : \mathbb{N}\rightarrow \mathbb{N}$ 是一个函数。则 $\mathbf{DTIME}(T(n))$ 是全体能被确定性单纸带图灵机在 $O(T(n))$ 时间内判定的语言之集合。在此基础上衍生出:
$\mathbf{P} := \cup_{c \geq 0} \mathbf{DTIME}(n^c)$ 为多项式时间可判定的复杂度类。
$\mathbf{EXP} := \cup_{c\geq 0} \mathbf{DTIME}(2^{n^c})$ 为指数时间可判定的复杂度类。
直觉上,随着时间的递增,可计算的问题应当越来越多,事实上有
定理 3.1.1(时间谱系定理). 设 $f(n), g(n)$ 是两个 time-constructable 的函数,满足 $f(n)\log f(n) = o(g(n))$。则
$$
\mathbf{DTIME}(f(n)) \subsetneq \mathbf{DTIME}(g(n))
$$
证明. 易见 $\mathbf{DTIME}(f(n))\subset \mathbf{DTIME}(g(n))$。现在要证明真子集关系,注意这个问题很像 $\mathbf{R}\subsetneq \mathbf{RE}$,只是把时间限制从 $\omega$ 改成了 $f(n)$。因此我们直接把该问题的对角线证明搬运过来。
设 $\mathcal{U}$ 是一个效率为 $O(T\log T)$ 通用图灵机。考虑如下语言 $L$:
- 在输入 $x$ 上:
- 用通用图灵机 $\mathcal{U}$ 模拟 $f(|x|)$ 步 $M_x$ 在 $x$ 上的运行。
- 如果 $M_x$ 停机,那么翻转其输出,否则拒绝。
根据定义 $L\in \mathbf{DTIME}(g(n))$。而若 $L\in \mathbf{DTIME}(f(n))$,设 $M_x$ 是一个在 $f(n)$ 时间内求解 $L$ 的图灵机。则 $M_x(x)$ 接受或拒绝都将推出对方,矛盾。$\blacksquare$
定义 3.1.2(非确定性时间复杂度类). $T : \mathbb{N}\rightarrow \mathbb{N}$ 是一个函数。则 $\mathbf{NTIME}(T(n))$ 是全体能被非确定性单纸带图灵机在 $O(T(n))$ 时间内判定的语言之集合。在此基础上衍生出 $\mathbf{NP} := \cup_{c\geq 0} \mathbf{NTIME}(n^c)$。
这个 $\mathbf{NP}$ 的定义和我们熟悉的版本不同。我们熟悉的版本是所谓的“多项式时间内验证”。实际上,这两个定义是等价的。
定理 3.1.2(类 $\mathbf{NP}$ 的刻画). 对于语言 $L$,$L\in \mathbf{NP}$ 当且仅当:存在一个图灵机 $M$(称作 verifier)和常数 $c$,对于任意的输入 $x$,都存在 $u \in \cup_{i\leq n^c} \Sigma^i$(称作 certificate),使得 $x\in L\Leftrightarrow M(x, u) = 1$。
证明. 必要性. 由于 $L$ 可被非确定性图灵机判定,只需用 certificate 指导走哪一个分支即可。
充分性. 非确定性图灵机可以猜一个 certificate。$\blacksquare$
至此显而易见 $\mathbf{P}\subset \mathbf{NP}\subset \mathbf{EXP}$,但都不知道是否是真子集。为了证明 $\mathbf{P} = \mathbf{NP}$,需要证明 $\mathbf{NP}$ 中最难的一众问题都是 $\mathbf{P}$ 的。为了比较难度,自然需要进行规约。
定义 3.1.3(Karp 规约). 称 $A\leq_p B$ 当且仅当存在多项式时间可计算的函数 $f : \Sigma^* \rightarrow \Sigma^*$ 使得 $\forall w, w\in A\Leftrightarrow w\in B$。
定义复杂度类 $\mathbf{NP}\text{-hard} := \{L : \forall L’\in \mathbf{NP}, L’ \leq_p L\}$ 以及 $\mathbf{NP}\text{-complete} := \mathbf{NP}\cap \mathbf{NP}\text{-hard}$。有若 $L\in \mathbf{NP}\text{-complete}$,$L\in \mathbf{P}$ 当且仅当 $\mathbf{P} = \mathbf{NP}$。这是一个经典的开放性问题。容易证明若 $\mathbf{P} = \mathbf{NP}$ 则 $\mathbf{EXP} = \mathbf{NEXP}$ 也成立。
而 NP 完全问题是存在的:
定理 3.1.3(Cook-Levin). $\mathrm{SAT}\in \mathbf{NP}\text{-complete}$,$\mathrm{3SAT}\in \mathbf{NP}\text{-complete}$。
证明. $\mathrm{SAT}\in \mathbf{NP}$ 是显然的,证据取作满足 CNF 的一组解即可。接下来证明 $\mathrm{SAT}\in \mathbf{NP}\text{-hard}$。为此,对于任意的 $\mathbf{L}\in \mathbf{NP}$,证明 $L\leq_p \mathrm{SAT}$。
这里的核心是考虑制作一个 CNF 来刻画 verifier 的格局序列。提示:
- 若 $M$ 的运行时间不超过 $n^c$,其格局序列的长度只有 $O(n^{2c})$,因此变量个数是多项式级别的。你可能需要这些变量:$i$ 时刻探头位置是否不超过 $j$,$i$ 时刻位置 $j$ 位置的字符是否是 $c$ 等。
- 你可能需要此类约束:$i$ 时刻探头位置不是 $j$ 且 $i$ 时刻和 $i + 1$ 时刻 $j$ 位置的字符相同,或 $i$ 时刻探头位置是 $j$ 且 $i + 1$ 时刻 $j$ 位置的字符符合转移函数给出的规律。显然,约束展开成 CNF 后是多项式个子句。
为了证明 $\mathrm{3SAT} \in \mathbf{NP}\text{-complete}$ 只需补充证明 $\mathrm{SAT} \leq_p \mathrm{3SAT}$。为此只需注意到如下的构造可以让 $u$ 复刻 $c_1\vee c_2$ 的值,进而在引入一些 3 变量子句的同时降低最大子句长度:
$$
(c_1 \vee c_2 \vee \neg u) \wedge (\neg c_1 \vee u) \wedge (\neg c_2 \vee u)
$$
$\blacksquare$
至于那些其他的 $\mathbf{NP}\text{-complete}$ 问题,留予读者自行探索。
注意若 $L\in \mathbf{NP}$,$\overline{L}\in \mathbf{NP}$ 是否成立是未知的。称 $\mathbf{coNP} := \{L : \overline{L}\in \mathbf{NP}\}$。显然 $\mathbf{P}\subset \mathbf{NP}\cap \mathbf{coNP}$,但是是否是真子集也未知。
另外可以定义 $\mathbf{coNP}\text{-hard}$ 和 $\mathbf{coNP}\text{-complete}$,显然若 $L\in \mathbf{NP}\text{-complete}$,则 $\overline{L} \in \mathbf{coNP}\text{-complete}$,因为 Karp 规约是当且仅当的。
其他结论
结论 1. 若 $\mathrm{SAT}\in \mathbf{P}$,则可以多项式时间构造一组解。
证明. 显然。
结论 2(Ladner). 若 $\mathbf{P}\ne \mathbf{NP}$,则 $\mathbf{NP} \setminus (\mathbf{P}\cup \mathbf{NP}\text{-complete}) \ne \varnothing$。
证明. $\color{red}{\text{Sorry.}}$
这类问题称为 $\mathbf{NP}\text{-intermediate}$ 问题。有潜力成为此类问题的包括质因数分解、图同构。
结论 3(非确定性时间谱系定理). 若 $f(n), g(n)$ time-constructable,且 $f(n + 1) = o(g(n))$,则 $\mathbf{NTIME}(f(n)) \subsetneq \mathbf{NTIME}(g(n))$。
证明. $\color{red}{\text{Sorry.}}$
空间复杂度
对于函数 $S : \mathbb{N} \rightarrow \mathbb{N}$,若图灵机 $M$ 在长度为 $n$ 的输入运行时使用的格子总数(不含输入纸带,即将输入纸带和工作纸带分开考虑)为 $S(n)$,则称 $M$ 的空间消耗为 $S(n)$。在非确定性的语境下,须统计各个分支的空间消耗最大值。
称 $S(n)$ 为 space-contructable,若可以在 $O(S(n))$ 空间内计算函数 $S(n)$。
定义 3.2.1(基本空间复杂度类). 令 $S(n)$ 是一个 space-constructable 的函数。
称 $L\in \mathbf{SPACE}(S(n))$,若存在空间消耗为 $O(S(n))$ 的确定性图灵机判定 $L$。
称 $L\in \mathbf{NSPACE}$,若存在空间消耗为 $O(S(n))$ 的非确定性图灵机判定 $L$。
下列断言都是显然的。
定理 3.2.1. $\mathbf{DTIME}(S(n))\subseteq \mathbf{SPACE}(S(n)) \subseteq \mathbf{NSPACE}(S(n))\subseteq \mathbf{DTIME}(2^{O(S(n))})$。
证明. 前两个关系都是平凡的。最后一个只能考虑把可能的格局变换建图然后在上面搜。$\blacksquare$
Remark. 将可能的格局变化建图是研究空间复杂度的重要工具。而且可以注意到确定性和非确定性在这里差距不大,无非只是:确定性图灵机的格局图是内向树,非确定性图灵机的格局图是有向无环图。
另外可以用对角线方法证明 $\mathbf{SPACE}$ 不同层之间也是真子集关系:
定理 3.2.2(空间谱系定理) 设 $f, g$ 是两个 space-constructable 的函数,满足 $f(n) = o(g(n))$,则
$$
\mathbf{SPACE}(f(n)) \subsetneq \mathbf{SPACE}(g(n))
$$
证明. 限制在 $g(|x|)$ 空间内模拟 $M_x$ 在 $x$ 上的运行至多 $2^{O(|x|)}$ 轮,若停机则翻转输出。若此语言显然属于 $\mathbf{SPACE}(g(n))$,但是若它属于 $\mathbf{SPACE}(f(n))$ 将导出矛盾。
定义 3.2.2(多项式空间复杂度类). $\mathbf{PSPACE} := \cup_{c\geq 0} \mathbf{SPACE}(n^c)$;$\mathbf{NPSPACE} := \cup_{c\geq 0} \mathbf{NSPACE}(n^c)$。
显然有 $\mathbf{NP}\subseteq \mathbf{PSPACE}$,因为可以用多项式空间枚举证据。但是不知道是否能取等。欲知是否不相等,还是希望找到一众最难的 $\mathbf{PSPACE}$ 问题。此处我们还是使用先前定义的 Karp 规约,容易证明 $A \leq_p B$ 则 $B\in \mathbf{PSPACE} \Rightarrow A\in \mathbf{PSPACE}$。
定义 $\mathbf{PSPACE}\text{-hard} := \{L : \forall L’\in \mathbf{PSPACE}, L’ \leq_p L\}$,$\mathbf{PSPACE}\text{-complete} := \mathbf{PSPACE}\cap \mathbf{PSPACE}\text{-hard}$。兹介绍一个著名的 $\mathbf{PSPACE}\text{-complete}$ 问题。
带量词布尔函数(QBF). $\psi = Q_1 x_1Q_2x_2\cdots Q_nx_n\phi(x_1, x_2, …, x_n)$,其中 $\phi(x_1, …, x_n)$ 是一个命题逻辑公式,$Q_1, …, Q_n\in \{\forall, \exists\}$。
永真带量词布尔函数问题(TQBF). $\mathrm{TQBF} := \{\psi\in \mathrm{QBF} : \psi\}$。
定理 3.2.3. $\mathrm{TQBF}\in \mathbf{PSPACE}\text{-complete}$。
证明. $\mathrm{TQBF}\in \mathbf{PSPACE}$. 直接搜索。
$\mathrm{TQBF}\in \mathbf{PSPACE}\text{-hard}$. 令 $L\in \mathbf{PSPACE}$,考虑用一个 QBF 刻画格局序列以证明 $L\leq_p \mathrm{TQBF}$。提示:假设 $L$ 可以用 $S(n)$ 空间判定,则
- 存在一个长度为 $O(S(n))$ 的公式 $\phi$,使得 $\phi(C, C’) = 1$ 当且仅当 $C$ 可以一步转移到 $C$。
- 尝试倍增 $\phi$,设计 QBF $\psi_i(C, C’)$ 表示存在 $C$ 到 $C’$ 的长度不超过 $2^i$ 的路径。有
$$
\psi_i(C, C’) = \exists C_m, \psi_{i - 1}(C, C_m) \wedge \psi_{i - 1}(C_m, C’)
$$ - 很遗憾的是这样每次长度都会倍增。于是考虑进行卡常:如此一来每递归一层长度只增加 $O(S(n))$
$$
\psi_i(C, C’) = \exists C_m\forall D_1\forall D_2 ((D_1 = C \wedge D_2 = C_m) \vee (D_1 = C_m \wedge D_2 = C’)) \rightarrow \psi_{i - 1}(D_1, D_2)
$$
最后有 $x\in L \Leftrightarrow \exists C, \mathrm{Accept}(C) \wedge \psi_{S(n)}(C_{init}(x), C)$,可以发现递归下来得到的 QBF 长度为 $O(S(n)^2)$ 级别。$\blacksquare$
注意,该问题的证明和确定性、非确定性无关。因此实际上有 $\mathrm{TQBF}\in \mathbf{NPSPACE}\text{-hard}$,但是 $\mathrm{TQBF}\in \mathbf{PSPACE}$,所以 $\mathbf{NPSPACE} = \mathbf{PSPACE}$。更细致地,有
定理 3.2.4(Savitch). 对于任意 space-constructable 的函数 $S(n)$,有 $\mathbf{NSPACE}(S(n))\subset \mathbf{SPACE}(S^2(n))$。
证明. 在格局图上倍增搜索即可。$\blacksquare$
最为节约空间的一类算法仅需使用对数空间。本小节研究对数空间的图灵机的相关结论。
定义 3.2.4(对数空间复杂度类). $\mathbf{L} := \mathbf{SPACE}(\log n)$;$\mathbf{NL} := \mathbf{NSPACE}(\log n)$。
这里,$\mathbf{NL}$ 也可以有一个 certificate-verifier 版本的定义。
定理 3.2.5(类 $\mathbf{NL}$ 的刻画). 一个语言 $L\in \mathbf{NL}$ 当且仅当存在 verifier $M(x, u)$,对于任意的输入 $x$ 都存在多项式长度的 certificate $u$,使得 $x\in L$ 当且仅当 $M(x, u) = 1$。注意,我们强制要求 verifier 只能从左到右读一次 certificate。
证明. 充分性. certificate 可以指导 NTM 每个时刻选择哪个分支,确实只需要从左到右读一次。
必要性. NTM 可以维护一个 $i$,然后猜 $u_i$ 是多少,再令 $i + 1$,从而复刻 $M(x, u)$ 的行为。$\blacksquare$
熟知 $\mathbf{L}\subseteq \mathbf{NL} \subseteq \mathbf{P}$。但是都不知道是否能取等。为此需要研究 $\mathbf{NL}\text{-complete}$ 和 $\mathbf{P}\text{-complete}$ 问题。然而 Karp 规约在这里又过于强了(不能保证规约之后还封闭在类中)。因此引入对数空间规约。
定义 3.2.5(隐式对数空间可计算). 称一个函数 $f: \{0, 1\}^*\rightarrow \{0, 1\}^*$ 是隐式对数空间可计算(implicitly logspace computable)的函数,若
- $f$ 长度是多项式的,即存在常数 $c$,$\forall x, |f(x)| \leq |x|^c$;
- $L_f := \{\langle x, i\rangle : f(x)_i = 1\} \in \mathbf{L}$,$L_{f}’ := \{\langle x, i\rangle : i \leq |f(x)|\} \in \mathbf{L}$。
定义 3.2.6(对数空间规约). 称 $B\leq_l C$ 当且仅当存在一个隐式对数空间可计算函数 $f$ 使得 $x\in B \Leftrightarrow f(x)\in C$。
容易证明若 $B\leq_l C, C\leq_l D$,则 $B\leq_l D$;若 $B\leq_l C, C\in \mathbf{L}$ 则 $B\in \mathbf{L}$。现在可定义 $\mathbf{NL}\text{-complete} := \{L \in \mathbf{NL} : \forall L’\in \mathbf{NL}, L’ \leq_l L\}$。
路径问题. $\mathrm{PATH} := \{\langle G, s, t\rangle : \text{$\exists$ a directed path in $G$ from $s$ to $t$}\}$
定理 3.2.6. $\mathrm{PATH}\in \mathbf{NL}\text{-complete}$。
证明. $\mathrm{PATH}\in \mathbf{NL}$. 只需要存当前路径长度、当前所在节点,然后猜下一个节点。走到 $t$ 立刻接受,路径过长就拒绝。
$\mathrm{PATH}\in \mathbf{NL}\text{-hard}$. 可以隐式对数空间计算格局图的邻接矩阵。$\blacksquare$
最后,仿照之前的研究模式,我们还希望探究一下 $\mathbf{NL}$ 和 $\mathbf{coNL}$ 是否相等。
定理 3.2.7. $\overline{\rm PATH}\in \mathbf{NL}$。因为 $\overline{\rm PATH}\in \mathbf{coNL}\text{-complete}$,所以 $\mathbf{NL} = \mathbf{coNL}$。
证明. 考虑让 verifier 知道 $s$ 能走到的所有点。记 $C_i$ 表示从 $s$ 出发走 $i$ 步能到的点的集合。则可以逐步构造以下证据:
- $v\in C_i$ 的证据. 给出一条路径即可。长度为 $O(n\log n)$
- 已知 $|C_{i - 1}| = c$ 的前提下,$v\notin C_i$ 的证据. 递增地给出 $C_{i - 1}$ 中的元素以及相应的证据,可检查 $v$ 和这些元素之间都没有边。长度为 $O(n^2\log n)$。
- 已知 $|C_{i - 1}| = c$ 的前提下,$|C_i| = c’$ 的证据. 递增地给出 $i = 1, 2, …, n$ 属于 $C_i$ 或者不属于 $C_i$ 的证据。长度为 $O(n^3\log n)$。
将上述证据顺次拼接成总长度约为 $\tilde{O}(n^4)$ 长的证据,即可诱导 verifier 知道 $|C_{n - 1}|$,进而给出 $v\notin C_n$ 的证据。$\blacksquare$
多项式层
考虑以下问题。
$\text{EXACT-INDSET} := \{\langle G, k\rangle : \text{the largest independent set of $G$ has size $k$}\}$
对于这个问题,难以给出 $\mathbf{NP}$ 或者 $\mathbf{coNP}$ 的算法。但是,存在图灵机 $M_1(x, u, v)$ 使得 $x\in \text{EXACT-INDSET}$ 当且仅当 $\exists u, \forall v, M_1(x, u, v)$(存在一个大小为 $k$ 的独立集,且任意大小超过 $k$ 的都不是独立集)。相当于我们拓展了 $\mathbf{NP}$ 的 certificate-verifier 版本的定义。
定义 3.3.1. 一个语言 $L\in \mathbf{\Sigma_i^p}$ 当且仅当:存在一个多项式时间的图灵机 $M(x, u_1, …, u_i)$ 和多项式函数 $q$,使得对于任意的 $x\in \{0, 1\}^*$,$x\in L$ 当且仅当
$$
\exists u_1 \in \{0, 1\}^{q(|x|)}, \forall u_2 \in \{0, 1\}^{q(|x|)}, …, M(x, u_1, u_2, …, u_i) = 1
$$
即需要检验 $i$ 个交替由 $\exists, \forall, …$ 限定的证据。定义 $\mathbf{\Pi_i^p} = \mathbf{co\Sigma_i^p}$,即需要检验 $i$ 个交替由 $\forall, \exists, …$ 限定的证据。
这里定义的类有一些归纳的结构。注意对于 $\mathbf{\Sigma_{i + 1}^p}$,需要验证
$$
\exists u_1 \in \{0, 1\}^{q(|x|)}, {\color{blue} \forall u_2 \in \{0, 1\}^{q(|x|)}, …, M(x, u_1, u_2, …, u_{i + 1}) = 1}
$$
蓝色的部分无非是一个 $\mathbf{\Pi_i^p}$ 的语言。因此可以看作在查询一个此语言的 oracle。
定义 3.3.2(Oracle TM). 给定函数 $f$,一个神谕机(Oracle Turing Machine)在常规的图灵机的基础上配备一条额外的纸带。该图灵机可以向这条额外的纸带写入 $x$,并通过转移到状态 $q_{query}$ 来获知 $f(x)$。
给定 $f$ 的 oracle,复杂度类 $\mathbf{A}$ 类的图灵机能求解的问题集合记作 $\mathbf{A}^f$。另外记 $\mathbf{A^B} := \{\mathbf{A}^f : f\in \mathbf{B}\}$。
定理 3.3.1. 以下断言成立:
- $\mathbf{\Sigma_i^p}, \mathbf{\Pi_{i}^p}\subseteq \mathbf{\Sigma_{i + 1}^p}\cap \mathbf{\Pi_{i + 1}^p}$。
- $\mathbf{\Sigma_{i + 1}^p} = \mathbf{NP}^{\mathbf{\Pi_i^p}}, \mathbf{\Pi_{i + 1}^p} = \mathbf{coNP}^{\mathbf{\Sigma_i^p}}$。
- $\cup_{i=1}^\infty \mathbf{\Sigma_i^p} = \cup_{i=1}^\infty\mathbf{\Pi_i^p}$。
证明. 根据定义显然成立。$\blacksquare$
据上方断言 3,定义 $\mathbf{PH} :=\cup_{i=1}^\infty \mathbf{\Sigma_i^p} = \cup_{i=1}^\infty\mathbf{\Pi_i^p}$。这个类称为多项式层(Polynomial Hierarchy)。我们关于 $\mathbf{P}$ 和 $\mathbf{NP}$、$\mathbf{NP}$ 和 $\mathbf{coNP}$ 的关系的猜想在多项式层中可以反映为 $\mathbf{\Sigma_i^p}\text{ v.s. }\mathbf{\Sigma_{i + 1}^p}$ 和 $\mathbf{\Sigma_i^p}\text{ v.s. }\mathbf{\Pi_i^p}$。
定理 3.3.2. 以下断言成立:
- 对于任意的 $i$,若 $\mathbf{\Sigma_i^p} = \mathbf{\Pi_i^p}$,则 $\mathbf{PH} = \mathbf{\Sigma_i^p}$。
- 若 $\mathbf{\Sigma_i^p} = \mathbf{\Sigma_{i + 1}^p}$,则 $\mathbf{PH} = \mathbf{\Sigma_i^p}$。
$\mathbf{PH} = \mathbf{\Sigma_i^p}$ 的现象称作多项式层坍缩。现在尚不知其是否发生。
证明. 注意用定理 3.3.1 的断言 2 可以推出 $1$ 的前件蕴含 $2$ 的前件:
$$
\mathbf{\Sigma_i^p} = \mathbf{\Pi_i^p} \quad \Rightarrow \quad \mathbf{\Sigma_{i + 1}^p} = \mathbf{NP}^\mathbf{\Pi_i^p} = \mathbf{NP}^{\mathbf{\Sigma_i^p}} = \mathbf{\Sigma_i^p}
$$
所以只需要证明断言 2。我们归纳证明 $\forall j \geq i, \mathbf{\Sigma_j^p}, \mathbf{\Pi_j^p}\subseteq \mathbf{\Sigma_i^p}$。当 $j = i + 1$ 时,结论成立。现在假设结论对于 $j - 1$ 成立,将证明对于 $j$ 也成立。这其实也很显然,因为
$$
\mathbf{\Pi_{j - 1}^p} = \mathbf{\Sigma_i^p} \quad \Rightarrow \quad \mathbf{\Sigma_j^p} = \mathbf{NP}^{\mathbf{\Pi_{j - 1}^p}} = \mathbf{NP^{\Pi_i^p}} = \mathbf{\Sigma_{i + 1}^p} = \mathbf{\Sigma_i^p}
$$
并起来立即得到 $\mathbf{PH} = \mathbf{\Sigma_i^p}$。$\blacksquare$
研究 $\mathbf{PH}$ 是否坍缩现在就变成了研究 $\mathbf{\Sigma_i^p}\text{-complete}$ 问题。
定理 3.3.3. 以下断言成立:
- 定义 $\mathrm{\Sigma_i SAT} := \{\psi = \exists u_1 \forall u_2 … Q_i u_i, \phi(u_1, …, u_i) : \psi\}$。则 $\mathrm{\Sigma_i SAT}\in \mathbf{\Sigma_i^p}\text{-complete}$。
- 若存在 $\mathbf{PH}\text{-complete}$ 问题,则多项式层坍缩。
- $\mathbf{PH} \subseteq \mathbf{PSPACE}$。
- 若多项式层不坍缩,则 $\mathbf{PH}\subsetneq \mathbf{PSPACE}$。
证明. 断言 1 显然,且 $\mathrm{\Sigma_i SAT}$ 可以用 TQBF 的算法在多项式空间内解决。注意这里 $i$ 是一个可以任意大的确定的常数,因此断言 3 成立。
断言 2 需要注意到 $\mathbf{PH}\text{-complete}$ 问题必是一个 $\mathbf{PH}$ 问题,进而是某个 $\mathbf{\Sigma_i^p}$ 问题。于是 $\mathbf{PH}$ 将会倒在第 $i$ 层。
假设断言 4 的反面,若 $\mathbf{PH} = \mathbf{PSPACE}$,则 $\mathrm{TQBF}$ 是 $\mathbf{PH}\text{-complete}$ 问题,推出 $\mathbf{PH}$ 坍缩,与前提矛盾。因此断言 4 成立。$\blacksquare$
Remark. 现在大多数人相信 $\mathbf{PH}$ 是不塌的。
布尔电路
另一种计算模型。一个 $n$ 输入 $1$ 输出布尔电路是一个 $n$ 源 $1$ 汇的 DAG。其中,每个节点的出度限制为 $1$,入度不超过 $2$。除开输入节点,每个节点都是与门 / 或门 / 非门之一。电路的大小指该 DAG 中的节点数量。
定义 3.4.1. 令 $T : \mathbb{N}\rightarrow \mathbb{N}$ 是一个函数。一个 $T(n)$ 大的电路族是一族布尔电路 $\{C_n, n \in \mathbb{N}\}$,其中 $C_n$ 有 $n$ 个输入,$1$ 个输出,满足 $|C_n| \leq T(n)$。
称一个语言 $L\in \mathbf{SIZE}(T(n))$,若存在一个 $T(n)$ 大的电路族满足 $\forall x\in \{0, 1\}^n, x\in L\Leftrightarrow C_n(x) = 1$。
可以发现,布尔电路和逻辑公式之间有着深刻的关联。考虑如下语言:
$\text{CKT-SAT} := \{\text{all satisfiable Boolean circuit}\}$
这给出了 Cook-Levin 定理的另一个证明:
定理 3.4.2. 如下断言成立:
- $\text{CKT-SAT}\in \mathbf{NP}\text{-complete}$。
- $\text{CKT-SAT} \leq_p \text{SAT}$。
证明. 断言 1 显然,可以用布尔电路识别 verifier 的格局序列。
断言 2 也显然,对于每一个 Gate 构造几个子句(对于或门 $v_i := v_j \vee v_k$,构造 $(\neg v_i \vee v_j \vee v_k) \wedge (v_i \vee \neg v_j) \wedge (v_i \vee \neg v_k)$ 状物)即可。$\blacksquare$
事实上,计算函数需要的布尔电路大小可能非常大。
定理 3.4.2. 几乎所有的 $f : \{0, 1\}^n\rightarrow \{0, 1\}$ 都需要 $\Omega(2^n / n)$ 大小的电路来计算。
证明. 这样的函数有 $w = 2^{2^n}$ 个。而 $S = 2^n / n$ 大的电路数量不超过 $\left(3\binom S 2\right)^S / S! = o(w)$ 个。$\blacksquare$
引理 3.4.3. 对于任意的 $f : \{0, 1\}^n$,只需要 $O(2^n)$ 大小的电路即可计算。
证明. 施归纳于电路输入个数。$f(x_1, …, x_{n - 1}, 0/1)$ 是两个 $n - 1$ 元函数,因此有电路大小上界 $T(n)$ 服从如下递推关系:
$$
T(n) = 2T(n - 1) + O(1)
$$
解得 $T(n) = O(2^n)$。$\blacksquare$
该引理可以加强至 $O(2^n / n)$,留作习题。这也就推出了电路大小的谱系定理:
定理 3.4.4(Non-Uniform Size Hierarchy Theorem). 对于任意的函数 $T, T’ : \mathbb{N}\rightarrow \mathbb{N}$,满足 $n < T(n) < T’(n) < 2^n / n$,且 $T(n)\log^2 T(n) = o(T’(n))$,则 $\mathbf{SIZE}(T(n))\subsetneq \mathbf{SIZE}(T’(n))$。
证明. 令 $l = \log T(n) + \log\log T(n) + C$,则几乎所有 $f : \{0, 1\}^l\rightarrow \{0, 1\}$ 都需要 $2^l / l > T(n)$ 大小的电路,但是最多也只需要 $O(2^l) = o(T’(n))$ 大小的电路即可计算。$\blacksquare$
从上述定义中可看出,布尔电路是一种非一致的计算模型。为了识别一个语言 $L$,你只需要给出一族专用的电路,这族电路中,不同的 $C_n$ 不必遵循相同的模式。因此,多项式大小的电路和多项式时间的图灵机并不是一个类(不必妄想用一个图灵机来模拟这一族电路,因为你首先要根据输入长度生成 $C_n$,而这样的算法未必存在)。定义 $\mathbf{P}\text{/poly} := \cup_{c\geq 0}\mathbf{SIZE}(n^c)$。
Remark. 我们补充一些关于这个复杂度类记号的说明。复杂度类 $\mathbf{A}\text{/$a(n)$}$ 实际上是指 $\mathbf{A}$ 类中的图灵机,但是在长度为 $n$ 的输入上会被给一个长度为 $a(n)$ 的建议。容易证明这个意义下的 $\mathbf{P}\text{/poly}$ 和多项式大小的电路族是完全一致的。
定理 3.4.5. $\mathbf{P} \subsetneq \mathbf{P}\text{/poly}$。
证明. $\mathbf{P}\subseteq \mathbf{P}\text{/poly}$ 是显然的,因为电路可以识别合法的格局序列。而 $\mathbf{P}\text{/poly}$ 中甚至包含不可判定的语言,比如
$$
\mathrm{UHALT} := \{1^x : \text{$M_x$ halts on $x$}\}
$$
因此确实有 $\mathbf{P}\subsetneq \mathbf{P}\text{/poly}$。$\blacksquare$
可以看到 $\mathbf{P}\text{/poly}$ 和 $\mathbf{NP}$ 的 certificate-verifier 版本定义略有相似之处,只是对于固定大小的输入都只能给定相同的证据,那么 $\mathbf{P}\text{/poly}$ 和 $\mathbf{NP}$ 的关系如何?答案是不知道,但是
定理 3.4.6(Karp-Lipton). 若 $\mathbf{NP}\subseteq \mathbf{P}\text{/poly}$,则 $\mathbf{PH} = \mathbf{\Sigma_2^p}$。
证明. 考虑 $\mathrm{\Pi_2 SAT}$ 这个问题。即 $\{\phi : \forall u, \exists v, \phi(u, v)\}$。其内层,$\{\langle\phi, u\rangle : \exists v\}$,是一个 $\mathbf{NP}$ 问题。由于 $\mathbf{NP}\subseteq \mathbf{P}\text{/poly}$,存在一族电路 $C_n$ 能判定此问题。而因为可判定意味着可以付出多项式的代价得到构造,因此存在一族电路 $C_n$ 使得 $\phi(C_n(\phi, u), u) = 1$。定义一个 verifier $M(x, c, u)$(第二个参数为电路的描述)为验证 $\phi(c(\phi, u), u)$ 是否为 $1$ 的图灵机,有
$$
x\in \mathrm{\Pi_2 SAT} \quad \Leftrightarrow \quad \exists c, \forall u, M(x, c, u) = 1
$$
得到 $\mathrm{\Pi_2 SAT}\in \mathbf{\Sigma_2^p}$,而 $\mathrm{\Pi_2 SAT}\in \mathbf{\Pi_2^p}\text{-complete}$,这蕴含 $\mathbf{\Pi_2^p} \subseteq \mathbf{\Sigma_2^p}$,进而 $\mathbf{\Pi_2^p} = \mathbf{\Sigma_2^p}$,因此 $\mathbf{PH}$ 将倒在第二层。$\blacksquare$
如果我们补充根据输入长度生成 $C_n$ 的算法,即定义
定义 3.4.2. 若存在图灵机,输入 $1^n$ 输出 $C_n$ 的描述,则:
- 若该图灵机是多项式时间的,则这一族线路称为 $\mathbf{P}$-uniform 电路族。
- 若该图灵机是对数空间的,则这一族线路称为 logspace-uniform 的。
则可以得到一个和图灵机效力等同的计算模型。
定理 3.4.6. 一个语言 $L$ 可以被多项式大小 logspace-uniform 电路族计算当且仅当 $L\in \mathbf{P}$。
证明. 必要性. 生成 $C_n$ 后模拟之即可。
充分性. 注意识别格局序列的电路的描述只需要用对数空间即可生成。$\blacksquare$
除了大小之外,电路还有另外一个属性是深度。这刻画了一个函数被并行计算的可行性。
定义 3.4.3. 称一个语言 $L\in \mathbf{NC^i}$,若存在 $c > 0$ 使得 $L$ 可以被一族大小为 $n^c$、深度为 $O(\log^i n)$ 的 logspace-uniform 电路族计算。
称一个语言 $L\in \mathbf{AC^i}$,若存在 $c > 0$ 使得 $L$ 可以被一族大小为 $n^c$、深度为 $O(\log^i n)$ 的 logspace-uniform 电路族计算。但这里,我们将取消与 / 或门的输入个数限制。即你可以同时求出任意多个输入的与 / 或。
另外定义 $\mathbf{NC} := \cup_{i=0}^\infty \mathbf{NC^i}, \mathbf{AC} := \cup_{i=0}^\infty \mathbf{NC^i}$
根据定义,$\mathbf{NC^i}\subseteq\mathbf{AC^i}\subseteq \mathbf{NC}^{i + 1}$。只知道 $\mathbf{NC}^0\subsetneq \mathbf{AC}^0 \subsetneq \mathbf{NC}^{1}$ 是真子集,其他是否是真子集都未知。
定理 3.4.7. $\mathbf{NC} = \cup_{k\geq 0} \mathbf{PT/WK}(\log^k n, n^k)\text{/poly}$。其中 $\mathbf{PT/WK}(f(n), g(n))$ 表示总时间为 $f(n)$,总运算量为 $g(n)$ 的并行算法。
证明. 因为可以带建议,所以就很显然了。$\blacksquare$
Remark. 这里有点 confusing,感觉 statement 里面应该是 $\mathbf{NC}\text{/poly}$。或者 non-uniform NC。
注意这里的 $\mathbf{PT/WK}\text{/poly}$ 比所谓的能高效并行计算的类还要强,然而即便如此求 dfs 树是不是 $\mathbf{NC}$ 的也是开放性问题。
关于低层次的 $\mathbf{AC}$ 与 $\mathbf{NC}$,还有若干可探究的结论。比如
定理 3.4.8. $\mathrm{XOR}\notin \mathbf{AC}^0$。
证明. $\color{red}{\text{Sorry.}}$
随机算法
定义 3.5.1(概率图灵机 / PTM). 有两套等价的定义:
- 图灵机有两套转移函数 $\delta_1, \delta_2$,每次转移等概率采用一种。
- 图灵机配备一条额外的只可从左往右读取单向纸带,纸带上给出了若干个随机比特。这种定义在后面证明时非常有用,我们将以 $M(\cdot, r)$ 来指定随机比特的观测值为 $r$。
称一个 PTM $M$ 在 $T(n)$ 时间内判定语言 $L$ 当且仅当它在 $T(|x|)$ 步内停机,并且有 $\Pr[M(x) = L(x)] \geq 2 / 3$。
定义 3.5.2(随机复杂度类). 对于语言 $L$,称
- $L\in \mathbf{BPTIME}(T(n))$,若它可以被一个 PTM 在 $O(T(n))$ 时间内判定。
- $L\in \mathbf{RTIME}(T(n))$,若存在 $O(T(n))$ 时间的 PTM 使得 $x\in L \Rightarrow \Pr[M(x) = 1]\geq 2/3$,$x\notin L\Rightarrow M(x) = 0$。
- $L\in \mathbf{ZTIME}(T(n))$,若存在期望 $O(T(n))$ 步停机的 PTM,一旦停机必然输出 $x\in L$ 的准确结果。
令 $\mathbf{BPP} := \cup_{c> 0}\mathbf{BPTIME}(n^c), \mathbf{RP} = \cup_{c > 0} \mathbf{RTIME}(n^c), \mathbf{ZPP} := \cup_{c > 0}\mathbf{ZTIME}(n^c)$。
这些类的关系为:
定理 3.5.1. 以下断言成立:
- $\mathbf{BPP} = \mathbf{coBPP}$。
- $\mathbf{RP}\subseteq \mathbf{BPP}, \mathbf{coRP}\subseteq \mathbf{BPP}$。
- $\mathbf{ZPP} = \mathbf{RP} \cap \mathbf{coRP}$。
证明. 前两个根据定义显然成立。
$\mathbf{ZPP}\subseteq \mathbf{RP}\cap \mathbf{coRP}$:根据马尔可夫不等式,$\mathbb{E}[T] = T(n) \Rightarrow \Pr[T \geq 4/3 T(n)] \leq 3/4$。因此只需要运行该 $\mathbf{ZPP}$ 算法 $cT(n)$ 步,若没有停机就拒绝,便得到 $\mathbf{RP}$ 的算法;若没有停机就接受,便得到 $\mathbf{coRP}$ 的算法。
$\mathbf{RP}\cap \mathbf{coRP}\subseteq \mathbf{ZPP}$:同时运行 $\mathbf{RP}$ 和 $\mathbf{coRP}$ 的算法 $M_1, M_2$,若 $M_1$ 输出 $1$ 即可断定 $x\in L$,若 $M_2$ 输出 $0$ 即可断定 $x\notin L$。简单讨论即可发现不可能出现 $M_1$ 输出 $0$,$M_2$ 输出 $1$ 的情况。$\blacksquare$
上述定义中要求常数概率成功,然而显然重复运行算法 $k$ 轮,就可以把错误率打到 $2^{-k}$ 级别(Error Reduction Theorem)。这个结论对于我们后续用 probabilistic method 证明随机算法类和其他类的关系是至关重要的。
现在我们想要探究:随机化到底是不是有用的。换言之,我们想探究 $\mathbf{BPP}$ 和 $\mathbf{NP}, \mathbf{PH}, \mathbf{P}\text{/poly}$ 之类的复杂度类关系如何。
定理 3.5.2. $\mathbf{BPP}\subseteq \mathbf{P}\text{/poly}$。
证明. 考虑 $L\in \mathbf{BPP}$。重复运行 $L$ 的 $\mathbf{BPP}$ 算法 $n + 1$ 轮,可以将错误率打到 $2^{-n + 1}$ 级别。因此,根据 union bound,对于随机生成的一组 $n + 1$ 列随机比特,存在一个输入,在输入上算法判断错误的概率仅为 $1/2$,因此存在一列随机比特使得长度为 $n$ 的输入上算法判断均不出错。将此列随机比特作为建议给出,即得 $\mathbf{BPP}\subseteq \mathbf{P}\text{/poly}$。$\blacksquare$
类似地,可以证明 $\mathbf{BP}\cdot \mathbf{NP} = \mathbf{NP}\text{/poly}$。这里 $\mathbf{A}\cdot \mathbf{B}$ 的意思是一切可以通过 $\mathbf{A}$ 中的图灵机规约到 $\mathbf{B}$ 的语言。
显然 $\mathbf{P}\subseteq \mathbf{BPP}$ 成立,但是不知道是不是真子集。$\mathbf{NP}$ 和 $\mathbf{BPP}$ 的关系也未知,但是知道
定理 3.5.3(Sipser-Lautemann). $\mathbf{BPP}\subseteq \mathbf{\Sigma_2^p}\cap \mathbf{\Pi_2^p}$。
证明. 因为 $\mathbf{BPP} = \mathbf{coBPP}$,所以只用证明 $\mathbf{BPP}\subseteq \mathbf{\Sigma_2^p}$。设 $L\in \mathbf{BPP}$,我们首先用 $k = O(n)$ 次投票取众数把错误概率卡到严格小于 $2^{-n}$(一共使用 $m = kn$ 个随机比特),然后考虑以下 $\mathbf{\Sigma_2^p}$ 中的 verifier:
$$
\exists u_1, …, u_k, \forall r, \bigvee_i M(x, u_i\oplus r)
$$
- 若 $x\notin L$,则根据 union bound,
$$
\Pr_r\left[\vee_{i = 1}^k M(x, r\oplus u_i) = 1\right]\leq k2^{-n} < 1
$$
因此 $\forall u_1, …, u_k, \exists r, \vee_i M(x, r\oplus u_i) = 0$。 - 若 $x\in L$,则
$$
\Pr_{u_1, …, u_k} \left[\forall r, \vee_{i=1}^k M(x, r\oplus u_i) = 1\right] \geq 1 - 2^m\cdot 2^{-kn} > 0
$$
因此 $\exists u_1, …, u_k, \forall r, \vee_i M(x, r\oplus u_i) = 1$ 成立。
综上所述 $x\in L \Leftrightarrow \exists u_1, …, u_k, \forall r, \vee_i M(x, r\oplus u_i) = 1$。于是 $\mathbf{BPP}\subseteq \mathbf{\Sigma_2^p}$。$\blacksquare$
当然,随机算法也可以限制空间。可定义 $\mathbf{BPL}, \mathbf{RL}$ 为相应的空间限制类。已经证明:
- $\mathbf{RL}\subseteq \mathbf{NL}$,因此 $\mathbf{RL}\subseteq\mathbf{P}$。(显然)
- $\mathbf{BPL}\subseteq \mathbf{P}$(可以直接求出输出的概率分布)
- $\mathbf{BPL}\subseteq \mathbf{L}^{3/2}$。
- $\mathrm{UPATH}\in \mathbf{L}$。
交互式证明
Warm-up. Bob 是一个色盲。现在 Bob 持有两张卡片,可能是全为红色或者一红一绿。Bob 想要通过询问 Alice 来推断两种情况之一,然而 Alice 意欲让 Bob 相信两张卡颜色不同。问 Bob 应当采取何种策略?
答案是 Bob 先向 Alice 出示两张卡,然后背地里随机地选择对换其位置或者保持原样,然后问 Alice 是否发生了对换,若 Alice 答错,立即断定为全红。
在上述情景中,有一方有无穷的计算能力,有一方的计算能力受限。注意到,若卡是一红一绿的,只要 Alice 配合,Bob 便可以知道结果,若卡是全红的,则无论 Alice 采取何种策略,在充分多次询问之后 Bob 几乎一定能知道结果。这类似于一个一致且完备的形式系统中,如果一个命题是真的,则证明者可以给出一个证明能够将其证明;如果一个命题是假的,则无论证明者有多强都不能证明该结果。
上述情景的(确定性版本)形式化如下:
定义 3.6.1($k$ 轮交互). 令 $f, g : \{0, 1\}^* \rightarrow \{0, 1\}^*$,$k$ 为一个正整数。$f$ 和 $g$ 在 $x\in \{0, 1\}^*$ 上的 $k$ 轮交互,记作 $\langle f, g\rangle(x)$ 是如下的字符串序列 $a_1, …, a_k$:
$$
\begin{aligned}
&a_1 = f(x), a_2 = g(x, a_1), \cdots \\
&a_{2i + 1} = f(x, a_1, …, a_{2i}), a_{2i + 2} = g(x, a_1, …, a_{2i + 1})
\end{aligned}
$$
$f$ 最后需要针对聊天记录做出判断。其判断记作 $\mathsf{Out}_f\langle f, g\rangle(x) := f(x, a_1, …, a_k)\in \{0, 1\}$。
定义 3.6.2(确定性交互式证明). 称一个语言 $L$ 可以被 $k$ 轮确定性交互式证明($L\in \mathbf{DIP}[k]$),若存在一个确定性的图灵机 $V$, 其在输入 $x, a_1, …, a_i$ 上的运行时间为 $\mathrm{poly}(|x|)$,可以和任意的函数 $P$ 进行 $k$ 轮交互,满足:
- $x\in L$ 则 $\exists P : \{0, 1\}^* \rightarrow \{0, 1\}^*, \textsf{Out}_V\langle V, P\rangle(x) = 1$(完备性);
- $x\notin L$ 则 $\forall P : \{0, 1\}^*\rightarrow \{0, 1\}^*, \textsf{Out}_V\langle V, P\rangle(x) = 0$(一致性)。
记 $\mathbf{DIP} := \cup_{c \geq 0}\mathbf{DIP}[n^c]$。
然而确定性交互式证明非常弱。
定理 3.6.1. $\mathbf{DIP} = \mathbf{NP}$。
证明. $\mathbf{NP}\subseteq \mathbf{DIP}$. 显然,只需将 verifier 取作 $\mathbf{NP}$ 问题中的 verifier。prover 发送问题的 certificate 即可。因此 $\mathbf{NP}\subseteq \mathbf{DIP}[1]$。
$\mathbf{DIP}\subseteq \mathbf{NP}$. certificate 为两人的完整聊天记录。verifier 只需要判断此聊天记录是否合法即可。$\blacksquare$
为了强化交互式证明的能力,可以考虑给 verifier 引入随机性(正如 warm-up 中的那样)。
定义 3.6.3(随机化交互式证明). 称 $L\in \mathbf{IP}[k]$ 当且仅当存在一个多项式时间概率图灵机能和任意函数 $P : \{0, 1\}^* \rightarrow \{0, 1\}^*$ 使得
- $x\in L$ 则 $\exists P, \Pr[\textsf{Out}_V\langle V, P\rangle(x) = 1]\geq 2/3$(完备性)
- $x\notin L$ 则 $\forall P, \Pr[\textsf{Out}_V\langle V, P\rangle(x) = 1]\leq 1/3$(一致性)
记 $\mathbf{IP} = \cup_{c\geq 0}\mathbf{IP}[n^c]$。
显然随机化交互式证明也可以做 error reduction。
定理 3.6.2. 将上方的 $2/3$ 改成 $1/2 + 1 / n^c$(或 $1 - 2^{-n^c}$),并将 $1/3$ 改成 $1/2 - 1 / n^c$(或 $2^{-n^c}$),类 $\mathbf{IP}$ 不会发生变化。
证明. 独立重复运行若干次协议然后主元素投票即可。
Graph Non-Isomorphism. 给定两个图 $G_1, G_2$,判断其是否不同构。这个语言记作 $\mathrm{GNI}$。
这个题和上方的 warm-up 如出一辙。以下是一个 $\mathbf{IP}$ 的算法:
- Verifier 随机一个 $i\in \{1, 2\}$,给 Prover 发送 $G_i$ 的一个随机的自同构。
- Prover 回答这是 $G_1, G_2$ 中的哪个图,并返回一个排列表示作用这个排列之后和原图等价。
如果 Prover 答对,立即判定图不同构。
$\overline{\text{3SAT}}$ 的交互式证明. 用交互式证明验证 $\overline{\text{3SAT}}$。这是一个 $\mathbf{coNP}$ 问题。
下面我们证明 $\#\text{3SAT}\in \mathbf{IP}$,此问题严格强于 $\text{3SAT}$。首先考虑代数化逻辑表达式,以便使用 Schwatz-Zippel 之类的工具:一个布尔表达式可以照此转化为一个多项式:
$$
\begin{aligned}
x_i\wedge x_j &\Rightarrow x_ix_j \\
x_i\vee x_j &\Rightarrow 1 - (1 - x_i)(1 - x_j) \\
\neg x_i &\Rightarrow 1 - x_i
\end{aligned}
$$
一个 3CNF $\phi$ 可以被转化做 3 次多项式的乘积 $g(x_1, …, x_n)$,其描述长度为 $O(m\log n)$。我们现在需要验证的问题形如
$$
k = \sum_{b_1\in \{0, 1\}}\cdots\sum_{b_n\in \{0, 1\}} g(b_1, …, b_n)
$$
我们的核心直觉是:
- V 可以自行验证低阶多项式的求值结果是否正确。
- V 可以用 Schwatz-Zippel 引理验证两多项式是否相等。
因此我们的 $\mathbf{IP}$ 协议流程如下:V 首先接收一个 P 发送的 $2^{\Theta(n)}$ 范围内的素数,并验证之。接下来 V 在 P 的引导下验证上述问题:
- 若 $n = 1$,V 可以自行完成验证,因为此时多项式度数很低。
- 定义如下一次多项式:
$$
h_1(x) := \sum_{b_2\in\{0, 1\}}\cdots\sum_{b_n\in \{0, 1\}} g(x, b_2, …, b_n)
$$
P 给 V 发送多项式 $s_1(x)$,并断定这就是 $h_1(x)$ 的等价形式。- (验证求值结果是否正确) P 验证是否有 $h_1(0) + h_1(1) = k$;
- (验证多项式是否正确) P 随机 $a\in \mathbb{F}_p$,然后递归验证 $h(a) = \sum_{b_2\in \{0, 1\}}\cdots \sum_{b_n\in \{0, 1\}} g(a, b_2, …, b_n)$ 是否成立。
这就是著名的 Sumcheck Protocol。
Remark. 以上两个例子代表了解决 $\mathbf{IP}$ 问题的两种直觉。
另外一个关于随机化的考虑方向是,原问题和 one-sided error 是否等价。显然,若将 $1/3$ 改成 $0$,则 $\mathbf{IP}$ 立刻退化成 $\mathbf{DIP}$(充分强的 prover 甚至能算出让你接受的随机种子,从而实现去随机化)。后面我们将看到把 $2/3$ 改成 $1$ 则 $\mathbf{IP}$ 的范围不会变化(这种可以将 $2/3$ 改成 $1$ 的性质,称作 Perfect Completeness)。
引理 3.6.3. $\mathbf{IP}\subseteq \mathbf{PSPACE}$。
证明. dfs 搜出接受概率最大的一个 prover 即可。$\blacksquare$
引理 3.6.4. $\mathrm{TQBF}\in \mathbf{IP}$,因此 $\mathbf{PSPACE}\subseteq \mathbf{IP}$。
证明. 将 TQBF 代数化。此时你需要验证的无非是
$$
1 = \sum_{b_1\in \{0, 1\}}\prod_{b_2\in \{0, 1\}}\cdots \sum_{b_{2k - 1}\in \{0, 1\}}\prod_{b_{2k}\in \{0, 1\}} g(b_1, …, b_k)
$$
套用 Sumcheck Protocol 即可 $\blacksquare$
至此,我们证明了 $\mathbf{IP} = \mathbf{PSPACE}$。
注意 Sumcheck Protocol 只会给出假阳性证明,不会给出假阴性证明。因此 $\mathbf{IP}$ 确实有 perfect completeness。
在上方的交互式证明中,证明的一致性依赖于随机比特是私有的。如果随机比特是公用的,那么交互式证明能够有何种计算能力?
定义 3.6.4(Arthur-Merlin 问题) 对于一切常数 $k$,定义 $\mathbf{AM}[k]$ 为 $\mathbf{IP}[k]$ 的如下子集:verifier 必须且仅能发送其使用的所有随机比特。
为了建立关于此类问题的直觉,我们首先给出
定理 3.6.5 $\mathrm{GNI}\in \mathbf{AM}$。
证明. 考虑定义如下集合:
$$
S := \{(H, \pi) : H\cong G_1 \vee H \cong G_2, \pi\in \mathrm{aut}(H)\}
$$
- 若 $G_1\not\cong G_2$,则 $|S| = 2n!$;
- 若 $G_1\cong G_2$,则 $|S| = n!$。
从中可抽象出如下问题:
Set Lower Bound Protocol. 定义 $S\subseteq \{0, 1\}^m$ 是一个集合,其中元素可以被均匀采样。存在一个数字 $K$,$2^{k - 2} < K \leq 2^{k - 1}$。
任务是:设计一个协议,若 $|S|\geq K$,则 verifier 高概率接受,若 $|S| \leq K / 2$,则 verifier 高概率拒绝。
定义 $\mathcal{H}_{m, k}$ 为从 $2^m$ 打到 $2^k$ 的两两独立的哈希函数:
$$
H_{m, k} := \{ax + b \pmod {2^k} : a, b\in \mathbb{GF}(2^m)\}
$$
将协议置为:
- V 随机选一个 $j\in \mathcal{H}_{m, k}$ 和一个 $y \in\{0, 1\}^k$,然后将 $h, y$ 发给 Prover。
- P 尝试找 $x\in S, h(x) = y$,然后将 $x$ 和 $x\in S$ 的证据发送给 V。
- V 验证 $h(x) = y$ 和 $x\in S$,接受当且仅当通过。
注意,若 $|S|\leq 2^k / 2$,定义 $p = |S| / 2^k$,对于固定的 $y$,定义事件 $E_x := \{h(x) = y\}$,则
- $\Pr[\exists x, E_x]\leq p$;
- 根据容斥原理,
$$
\Pr\left[\cup_x E_x\right]\geq \sum_x \Pr[E_x] - \frac{1}{2}\sum_{x_1\ne x_2} \Pr[E_{x_1}\cap E_{x_2}] = p - \frac{|S|(|S| - 1)}{2}2^{-2k}\geq \frac 34 p
$$
可以看到这里两种情况已经出现了概率的 separation。有当 $|S| \geq K$ 时,成功概率至少为 $3K / 2^{k + 2}$,当 $|S|\leq K / 2$ 时,成功概率至多为 $K / 2^{k + 1}$。只需要独立采样若干轮,即可高概率将两种情况分开。
最后罗列一些 $\mathbf{AM}$ 的其他结论。我们这里定义 $\mathbf{MA}$ 为 Merlin 先发送消息,$\mathbf{MAM}$ 为 Merlin 先发送消息的 3 轮通信。
引理 3.6.6. $\mathbf{MAM} = \mathbf{AM}$。
证明. $\mathbf{AM}\subseteq \mathbf{MAM}$ 是显然的:不论第一轮 Merlin 说了什么,Arthur 都摆烂即可。
$\mathbf{MAM}\subseteq\mathbf{AM}$:Arthur 可以用多项式次 Error Reduction 把概率加强到无论第一轮 Merlin 说了什么都可以高概率正确。所以已知 $\mathbf{MAM}$ 的协议,$\mathbf{AM}$ 的协议为 Arthur 首先给 Merlin 摇一堆随机种子,然后 Merlin 把他要说的两句话告诉 Arthur,Arthur 再进行计算。$\blacksquare$
引理 3.6.7. $\mathbf{MA}\subseteq \mathbf{AM}$。
证明. 因为 $\mathbf{MA}\subseteq \mathbf{MAM} = \mathbf{AM}$(不论第二次 Merlin 说了什么都直接摆)。$\blacksquare$
推论 3.6.8. $\mathbf{AM} = \mathbf{AM}[2]$。注意这里 $\mathbf{AM} = \cup_c \mathbf{AM}[c]$,即常数次交互的 $\mathbf{AM}$。
证明. 用上方两引理归纳即可。$\blacksquare$
定理 3.6.9. $\mathbf{MA}$ 和 $\mathbf{AM}$ 都可以做到 perfect completeness。
证明. $\color{red}{\text{Sorry.}}$(使用 $\mathbf{BPP}\in \mathbf{PH}$ 的 trick,Merlin 先发送一众 $u_1, …, u_k$)
定理 3.6.10. $\mathbf{AM} = \mathbf{BP}\cdot \mathbf{NP}\subseteq \Pi_2^p$
证明. $\color{red}{\text{Sorry.}}$
定理 3.6.10. 若 $\mathrm{GI}\in \mathbf{NP}\text{-complete}$ 则 $\mathbf{AM} = \mathbf{PH} = \mathbf{\Sigma_2^p}$。
证明. 若前提发生,则 $\mathrm{GNI}\in \mathbf{coNP}\text{-complete}$,所以 $\mathbf{coNP}\in \mathbf{AM}$。因此
$$
\begin{aligned}
\mathbf{\Sigma_2^p} &= \exists\mathbf{coNP} \\
&\subseteq \exists\mathbf{AM} \\
&= \mathbf{MAM} \\
&\subseteq \mathbf{\Pi_2^p}
\end{aligned}
$$
$\blacksquare$
定理 3.6.11. 若 $\mathbf{IP}\subseteq \mathbf{P}\text{/poly}$ 则 $\mathbf{IP} = \mathbf{MA}$。
证明. 若 $\mathbf{IP} \subseteq \mathbf{P}\text{/poly}$,则 $\mathrm{TQBF}$ 的 prover(显然是 $\mathbf{PSPACE}$ 的)可以被换成一个电路。那么 Merlin 把这个电路发给 Arthur,Arthur 拿着这个电路自己进行交互式证明即可。$\blacksquare$
附录
开放性问题
为了防止考场上挑战图灵奖,这里收集一些(截至文章写作时尚开放的)开放性问题。
- $\mathbf{P}$ 和 $\mathbf{NP} \cap \mathbf{coNP}$ 是否相等未知。
- $\mathbf{PH}$ 是否坍缩未知(回忆什么将会导致 $\mathbf{PH}$ 坍缩),$\mathbf{PH}$ 和 $\mathbf{PSPACE}$ 是否相等未知。
- $\mathbf{L}$ 和 $\mathbf{NL}$ 是否相等未知;$\mathbf{NL}$ 和 $\mathbf{P}$ 是否相等未知。
- $\mathbf{NP}$ 是否是 $\mathbf{P}\text{/poly}$ 的子集未知。
- $\mathbf{P}$ 是否是 $\mathbf{BPP}$ 的真子集未知。$\mathbf{NP}$ 和 $\mathbf{BPP}$ 的关系未知。
练习和补充结论
习题 1. 设 $f(n) = o(n\log n)$,则 $\mathbf{DTIME}(f(n)) = \mathbf{REG}$。这也表明 $\mathbf{DTIME}(f(n)) = \mathbf{DTIME}(n)$。
习题 2. $\mathrm{2SAT}\in \mathbf{NL}\text{-complete}$。
习题 3. 对于任意的 $f : \{0, 1\}^n$,只需要 $O(2^n / n)$ 大小的电路即可计算。
证明. 使用一种类似于四毛子的技术。取参数 $t$,搭建所有 $t$ 元函数的电路,然后根据后 $n - t$ 个输入决定 $f(\cdot, \cdots, \cdot, x_{t + 1}, …, x_{n})$ 是哪一种。如图所示
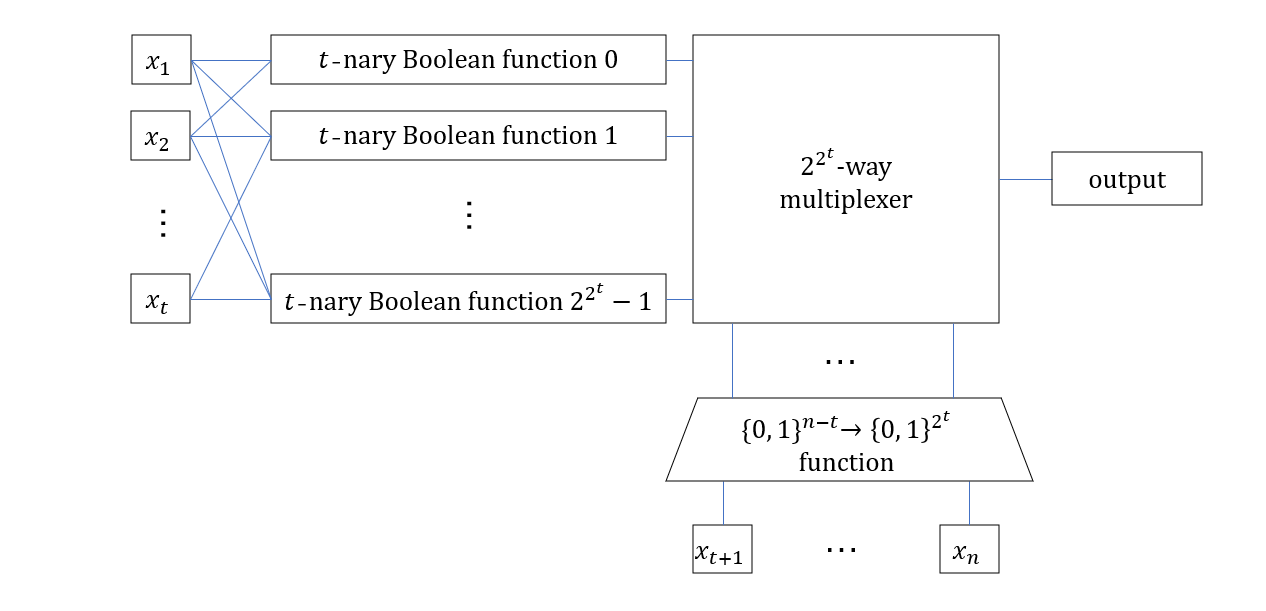
注意可以构造大小为 $O(2^t2^{2^t})$ 大小的多路复用器。因此搭建上述电路所需门数量上界 $T(n)$ 服从递推关系
$$
T(n) \leq 2^{2^t} T(t) + 2^t T(n - t) + O(2^t2^{2^t})
$$
取 $T = \log_2 n - 1$ 解得 $T(n) = O(2^n / n)$。$\blacksquare$