FLUTE Algorithm
本文收录于 EDA 论文选读。
TL;DR
一个 RSMT 的并不精确的高速启发式算法。
- 对于 $n\leq 9$ 的 net,打表;
- 对于更大的 net,设计启发式的分治。
由于我刚入门,所以想先对这个学科研究的侧重点和方法论有一个大致的理解。因此,本文的构建中极其注重算法的动机。关于侧重点和方法论,有如下初步的结论:
- 可能需要注意到实践中某个量并不大;
- 有很多小数据上的 adhoc;
- 需要考虑如何充分利用算力(e.g. 卡常,GPU 加速);
- 可能需要设计不那么有道理的启发式算法,挖一些因子。
基本直觉
RSMT 问题是 EDA 领域的经典问题,用于在 routing 阶段为每个 net 生成通路。其定义如下:
定义 1 (Rectilinear Steiner Minimal Tree). 给定 $n$ 个 $\mathbb{R}^2$ 上的点 $\{(x_i, y_i)\}_{i=1}^n$,用水平或垂直的线段将所有点连通,最小化线段总长度。
当然,在现实中我们可能通常需要多次查询(量级在 $10^{5}\sim 10^6$)小规模问题($n$ 平均为 $4$ 左右,最大为 $100+$)的答案。上面的参考数据来自 ISPD98 benchmark。因此我们可能不希望使用那个众所周知的状压 DP 或者模拟退火之类单次非常慢的算法。
关于这个问题,有以下直觉,这里略去证明,如感兴趣可以自行参考相关文献:
- $\mathrm{RSMT}\in \mathbf{NP}\text{-complete}$;
- 对于一个 RSMT 问题的实例,存在一个最优的 Steiner Tree,满足每一条边都在 Hannan Grid 上(Hannan Grid 是由 $x = x_i$ 和 $y = y_i$ 织成的网格)。
我们已经提到了 RSMT 问题存在 Hannan Grid 上的解。不妨设 $x_1 \leq x_2 \leq \cdots \leq x_n$ 是所有横坐标排序之后的结果,$y_1 \leq y_2 \leq \cdots \leq y_n$ 类似。那么,任意一个 RSMT 问题的实例可以用一个长度为 $n$ 的 position sequence $s_i$ 和两个长度为 $n - 1$ 的数组 $h_i$ 和 $v_i$ 刻画:其中,$s_i$ 表示 $x_i$ 对应的 $y_i$ 是第几大的;$h_i$ 和 $v_i$ 分别表示网格第 $i$ 列的宽和第 $i$ 行的高。
如此一来,为了计算任意一个 Hannan Grid 上的 Steiner tree 的总边长,我们惟需考察有多少边水平穿过了第 $i$ 列(记作 $\alpha_i$)以及有多少边竖直穿过了第 $i$ 行(记作 $\beta_i$),然后便有
$$
L = (\boldsymbol{h}, \boldsymbol{v})^\top (\alpha, \beta)
$$
这样的 $(\alpha, \beta)$ 称作 wirelength vector。如下图所示,下面的三个 Steiner tree 的 wirelength vector 分别是 $(1, 2, 1, 1, 1, 2), (1, 1, 1, 1, 2, 3)$ 和 $(1, 2, 1, 1, 1, 1)$。
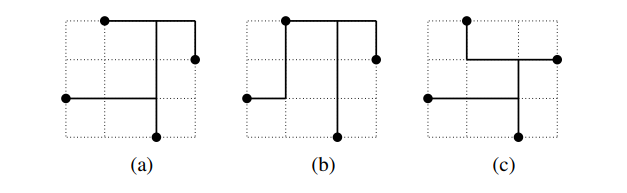
注意,如果一个 wirelength vector $\boldsymbol{w}$ 偏序(i.e. 每一维都大于等于,其中至少有一维严格大于)了另一个 wirelength vector $\boldsymbol{w}’$,那么 $\boldsymbol{w}$ 对应的 Steiner tree 永无可能成为最优的 Steiner tree。比方说此处的 $(a)$ 状的树,无论如何都不可能是最优的 Steiner tree。一切不偏序其他向量的 wirelength vector 即可能产生最优的 Steiner tree 的向量称作 potentially optimal wirelength vector (POWV),对应的 Steiner tree 称作 potentially optimal Steiner tree(POST)。
直觉上,可能的 POWV 并不多。因此我们可以打一个表来描述任意一个 position sequence 对应的全部 POWV 和 POST,然后在上面快速查询。
速查表的生成
现在我们尝试生成 $n\leq 9$ 的全部 POST 和对应的 POWV。因为点数非常少,所以树的结构并不多样。
生成 POWV 和 POST 的基本思想是递归。可以从两个方向考虑这件事情:
- boundary compaction,即考虑某一条边界(如 $x = x_1$)上的点应当如何与其余的点连通。一个简单的想法是,将这些点都投影到 $x = x_2$ 上,并在压缩后的网格上求出 POST,然后连接原始点和投影点。
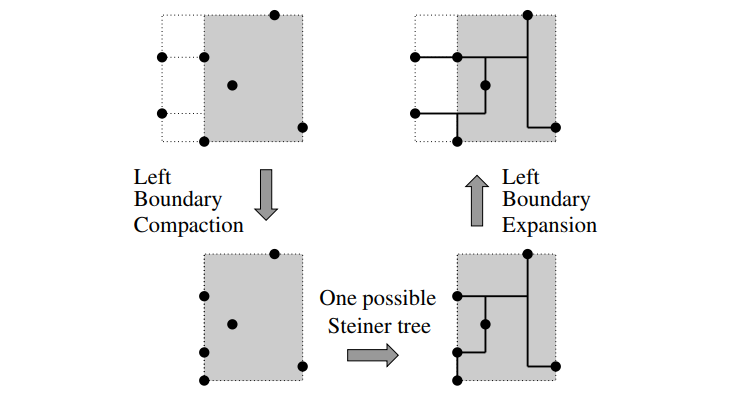
- connect adjacent pins,即将一个边界上的点全都连接起来然后在上面指定一个接入点。
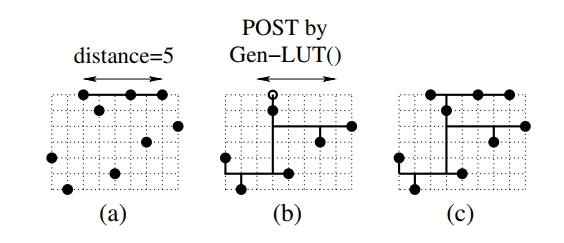
显然,通过 compaction 操作未必能准确地生成 POWV。对于网格 $G$(配上格点上的引脚),称其是 compectable 的,若可以通过上述流程求出其全部 POWV(注意,在做 boundary compaction 后,求子问题的 POST 不一定要继续使用 compaction,而是务必保证求出准确的 POST)。然而,有一些特殊的实例上可以做这样的操作。我们将逐渐揭示何种网格上可以做这种操作:
- 如果存在一个网格边界,上方有且仅有一个点,则该网格是 compactable 的。 只需考虑该点在何处接入除开该点以外的 steiner tree。如果该位置不是正投影,将该路径沿着矩形对角线方向翻折。
- 如果存在一个网格的角,其上有一个点,且相邻两个边界上均仅有一个另外的点,则该网格是 compactable 的。 这也是一个简单的调整,只需考虑涉及到的三个点之间如何连接和如何接入剩余部分的 steiner tree。
- 如果一个网格的边界上至多有六个点,则该网格是 compactable 的。 不难发现边界上至多有六个点则必然落入上述两种情况之一。
这样一来我们已经解决了一切边界上至多有 $6$ 个点的问题。顺带可以解决一些剩余的情况:
- 若 $n$ 个点全部在网格的边界上,那么每个 POWV 一定对应一个完全在边界的 POST。
- 剩余情况($8\leq n$,且至少有 $7$ 个都在边界上)可以用 connect adjacent pins 解决。证明想必非常暴力,这里先不看。
实验表明,这样求出的 POWV 基本上只有 $10\sim 10^2$ 量级(对于 $9$ 度的 net,平均 $30+$ 个,最大 $70+$ 个)。
常数优化
system 魅力时刻。考虑从两个方向压榨计算机的性能:
- 空间常数优化;
- 时间常数优化。
有点太细了,先不看。
关于空间,基本上有下面的这些 idea(论文中的,和我猜的):
- 一开始的 position sequence 都是 permutation,这意味着初始时四个边界上只有一个点,因而网格是可以沿着四个方向上 compact。容易发现,compact 之后有十六种初始网格会对应到同一个网格(取决于最外一圈的点和次外一圈的点);
- position sequence 做逆行、倒映、或两者之复合后得到的 position sequance 的 POWV 可以由其推出。
这样一来,看起来我们至少能把空间压缩几十倍($(1 - \epsilon) \cdot 16\cdot 4$)。
关于时间,我们可以考虑:
- 注意这里是小数据,加法的代价比乘法的代价小的多,所以我们用加法来算点乘,此外注意条边至少要被经过一次,因此可以预处理网格的长加宽,从而节约 $2(n - 1)$ 个加法。
- 好像还有个递推算的,没怎么看懂,但感觉不是很重要。
我感觉这个在现代处理器 / GPU 上应该用处没那么大,所以先不管了。
处理度数更大的 net
至此,对于低于 $9$ 度的 net,我们已经打好了表。为了强行利用这个表求解更大的问题,我们需要对度数较大的 net 构造一种分治策略。
然而很不幸的是对于 steiner tree 问题并不存在一个很好的分治策略。下面的结论非常平凡,但已经是我们能有的比较好的直觉:
定理 1. 若存在 $(x, y)$ 使得所有引脚要么只在 $(x, y)$ 的一、三象限,要么只在二、四象限,那么将横坐标不超过 $x$ 的引脚集合记作 $L$,其余记作 $R$,则 $\mathrm{RSMT}(L\cup R) = \mathrm{RSMT}(L\cup\{(x, y)\})\cup \mathrm{RSMT}(R\cup\{(x, y)\})$。
因此,我们被迫牺牲准确率,转而思考一些 heuristics。下面是一个比较直观的启发式算法框架:
- 将 net 按照某个水平边 $y_r$ 分成上下两部分。注意这个划分不一定是均分,而是在 $\delta n$ 到 $n - \delta n + 1$ 之间去找一个估计比较优的。
- 递归下去找两部分(都包含 $x_r, y_r$)的 RSMT,然后合并,并用某种方法消除冗余边。
关于划分的选择,我们考虑对划分点 $r$ 定义一个分数 $S(r)$,用于鼓励以下两个直觉上让算法得到更好的 steiner tree 的要点:
- 算法选择一个分界线,在最优的 steiner tree 中确实只有一个桥经过此分界线。 比如你可以要求网格在分界点附近纵向跨度大,横向跨度小以促进只有一个纵向的桥跨过此点,左右两侧横向连接。
- 算法选择一个分界线,使得以此划分后斯坦纳树的估计值较小。 比如你可以要求分界点尽量在网格中间,以及划分后两部分的 HPWL(half-perimeter wirelength 即包围盒包周长,常用于估计 wirelength)尽量小。
受此启发,原论文将 $S(r)$ 定义做
$$
\begin{aligned}
S(r) &= S_1(r) - \alpha S_2(r) - \beta S_3(r) - \gamma S_4(r) \quad \text{where} \\
S_1(r) &= y_{r + 1} - y_{r - 1} \\
S_2(r) &= \begin{cases}
2(x_3 - x_2) & \text{if $s_r = 1$ or $2$} \\
x_{s_r + 1} - x_{s_r - 1} & \text{if $3\leq s_r \leq n - 2$} \\
2(x_{n - 1} - x_{n - 2}) & \text{if $s_r = n - 1$ or $n$}
\end{cases} \\
S_3(r) &= \left|s_r - \frac{n + 1}{2}\right|\times \overline{h} + \left|r - \frac{n + 1}{2}\right|\times \overline{v} \\
S_4(r) &= \mathrm{HPWL}(L) + \mathrm{HPWL}(R)
\end{aligned}
$$
并实验得出取 $\alpha = 0.3, \beta = 7.4/(n + 10), \gamma = 4.8 / (n - 1)$ 比较优。
Remark. 我个人觉得这部分非常之丑,尤其是 $S_2$ 这个诡异的分类讨论和这个意义不明的 $S_3$。但是我也没精力做消融实验。
最后,为了合并两部分的 steiner tree,有以下一些直观的思路:
- 直接破坏掉环(显然,合并后至多出现一个环)。
- 如果重合部分涉及到的邻居很少,甚至可以在前面打的表里查一下这部分最优的 steiner tree 长什么样子。
另外我们可以引入一个参数 $A$ 来平衡时间-准确度的 tradeoff。参数 $A$ 表示在本次递归中找 $A$ 个分界线做递归。每次递归下去后将 $A$ 置为 $\max(A/2, 1)$。