Revision | 随机算法
Abstract. 随机算法的复习笔记。没有复习完,缺的内容用 $\color{red}{\text{Sorry.}}$ 标出,暂时可以补充参考 这个 Note
现在缺少的部分
- 前面几章比较初等的随机算法;
- Lovasz Local Lemma 里面那个数据包路由的证明;
- 网络可靠性里面大割不多的证明;
- The Power of Two Choices;
- 随机图 Hamilton 回路的证明;
- 随机图巨连通块 $c > 1$ 一侧的证明;
- 快速时间的集中性;
- 一些关于 coupling 的理解。
Schwatz-Zippel 引理和类似结论
$\color{red}{\text{Sorry.}}$
概率方法
经典结论
- 某事件发生的概率大于 $0$ 蕴含存在性。
- 某量的期望为 $E$ 蕴含存在其最大值不小于 $E$。
本节列举一些概率方法证明的经典结论,略去无关宏旨的细节。
MAX3SAT. $\mathrm{MAX3SAT}$ 问题的答案不小于 $\frac 78 m$,其中 $m$ 为子句数。
直接随机,求满足的子句个数的期望。
Remark. 维护条件期望,可得构造近似解的算法。
Ramsey 数下界. $R(k, k) \geq 2^{(k - 1) / 2}$。
随机染色,union bound 存在三元环的概率。
最大割. 一个图的最大割定大于等于其边数之半。
均匀随机一个点是否在割集之中,计算割的期望。
最大独立集 一个图的最大独立集大小定不小于 $\sum\limits_{v}\frac{1}{\mathrm{deg}(v) + 1}$。
随机排列 $\pi$,将 $v$ 选入独立集若它是邻域内的最小值,计算这样得到的独立集大小的期望。
平面嵌入最小交叉数. 令 $c(G)$ 是将 $G$ 嵌入 $\mathbb{R}^2$ 边的最小交叉数。则 $c(G) \geq |E| - 3|V| + 6$,且对于 $|E| > 4|V|$ 的图都有 $c(G) \geq \frac{|E|^3}{64 |V|^2}$
平面图的欧拉公式为 $|S| = |E| - |V| + 2$,用 $|S|$ 来统计边数,每个面至少是 $3$ 条边,可知 $3|S| \geq 2|V|$。代入得到 $|E|\leq 3|V| - 6$。
对于前一个断言,用欧拉公式证明。通过将交点也改造成一个点,可以得到一个平面图。将新图的数据代入此前所得不等式:
$$
|E| + 2c(G) \leq 3(|V| + c(G)) - 6 \quad \Rightarrow \quad c(G) \geq |E| - 3|V| + 6
$$
用概率方法加强此结论。以概率 $p$ 保留每个点得到诱导子图 $G’$,有每条边保留的概率为 $p^2$,每个交点保留的概率为 $p^4$
$$
\begin{aligned}
p^4 c(G) &= \mathbb{E}[c(G’)] \\
&\geq p^2|E| - 3p|V| + 6
\end{aligned}
$$
得到
$$
c(G) \geq \frac{p |E| - 3|V|}{p^3}
$$
接下来随便调整一下 $p$ 即可($p = \frac{4|V|}{|E|}$)。
开关问题. 对于一个 $n\times n$ 的 0/1 矩阵,可以对其进行整行、整列的翻转。则存在一种操作方案使得 $1$ 的个数为如下级别(无论初状态如何)
$$
\frac{n^2}{2} + \sqrt{\frac{1}{2\pi}} n^{3/2} + o(n^{3/2})
$$
考虑对于行,随机操作。对于列,启发式地操作(如果 $1$ 的个数少于一半,则操作)
这样一来,根据中心极限定理,$1$ 的个数和 $0$ 的个数之差的绝对值(也是第二步操作的期望收益的两倍)相当于是在平面上做 $n$ 步随机游走,停止位置的绝对值。套用结论知道这东西集中在某个 $C\sqrt n$ 附近。
周长和色数. 一个图的周长(Girth)为其最小环的大小,色数的定义是众所周知的。直觉上,这两个量是拮抗的。但是实际上,对于任意的 $k, l$,存在一个图,其周长 $\geq l$,色数 $\geq k$。
众所周知,若最大独立集不超过 $y = n / k$,则色数必超过 $k$。
考虑在 $G_{n, p}$ 上统计小环的个数 $c$ 和大独立集 $s$ 的个数(也是存在小环和大独立集的概率上界):
$$
\begin{aligned}
c &= \sum_{i=2}^{l - 1}\binom{n}{i}p^{i} = O\left((np)^{l - 1}\right) \\
s &= \binom{n}{y}p^{\binom{y}{2}} = O\left(n^y e^{-p\binom y2}\right)
\end{aligned}
$$
发现难以单靠调整 $p$ 将这两个量同时控制在 $o(1)$ (前者要求 $p = o(1 / n)$,后者要求 $p = \omega(1 / n)$)。但我们可以做如下操作:
注意到若存在小环个数不超过 $n / 2$,独立集大小不超过 $y$ ($\star$)的图 $G$,从中删去至多 $n / 2$ 个点以破坏掉所有的小环得到 $G’$,独立集大小不会增加,$G’$ 便是符合条件的图!因此令 $p = n^{-1 + \frac{1}{l}}$,这可以将 $s$ 控制在 $o(1)$,将 $c$ 控制在 $o(n)$。根据 markov 不等式,有以 $o(1)$ 概率,图中的小环的数量超过 $n / 2$ 或独立集大小超过 $y$,因此满足($\star$)的图确实存在,进而满足题目条件的图存在。
单调多数决电路. $\mathrm{MAJ}\in \mathbf{mNC}^1$,此复杂度类表示只允许使用与、或门 $\mathbf{NC}^1$ 的电路,详情参见 Complexity Zoo。
首先显然存在 $\mathrm{MAJ}_3(x_1, x_2, x_3)$ 的常数深度电路。这个电路有如下 probability amplification 之功用:若 $\Pr[x_i = 1] = p$,则
$$
\Pr[\mathrm{MAJ}(x_1, x_2, x_3) = 1] = 3p^2(1 - p) + p^3
$$
画出这个迭代的图像,发现它能将 $\frac 12 \pm \varepsilon$ 的概率分别往 $0, 1$ 方向强化。不失一般性设电路输入个数为奇数,则若应输出 $1$,$1$ 的频率至少是 $p = \frac 12 + O\left(\frac 1n\right)$。我们随机搭建如下电路(上面是一个满三叉树,每个节点是一个 $\mathrm{MAJ}_3$ 的电路,最下层叶子的三个引脚随机地连接输入)
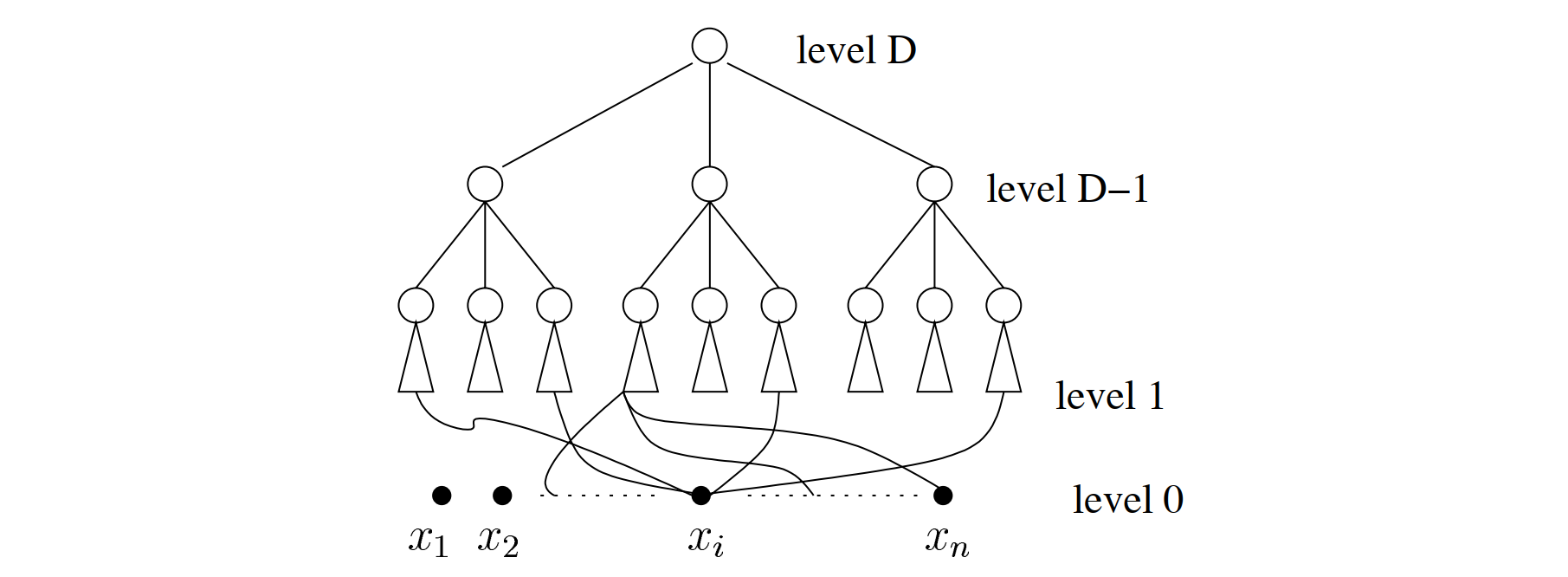
只需证明通过 $O(\log n)$ 迭代,能将概率 $p$ 强化至 $1 - O(2^{-n})$,即可用 union bound 指出:对于形如这般的随机电路,存在一个输入答案错误的概率小于 $2^n\cdot 2^{-n} = 1$,进而存在一个这种电路能够计算 $\mathrm{MAJ}$。
迭代的分析是琐碎且容易的,这里不写,总之确实可以证明 $\log n$ 次就可以将错误率加强到 $o(2^{-n})$ 级别。
Lovász Local Lemma
直觉上,如果一系列坏事件发生概率不太高,而且没那么独立,则可能都不发生。
定理 1(Lovász Local Lemma). 设 $A_1, …, A_n$ 是一系列坏事件。$\Pr[A_i] \leq p$,且每个 $A_i$ 独立于除 $d$ 个 $A_j$ 之外的所有事件。若 $ep(d + 1) \leq 1$,则
$$
\Pr\left[\bigcap_{i=1}^n \overline{A_i}\right]\geq 0
$$
证明. 无非是证明对于任意的 $i = 1, 2, …, n$
$$
\Pr\left[A_i | \bigcap_{i=1}^{i - 1} \overline{A_i}\right] \leq k < 1
$$
我们施归纳于事件数量 $m$,归纳证明这个上界是 $1 / (d + 1)$。
令 $D_i$ 是和 $S_i$ 不独立的那至多 $d$ 个事件。令 $S:= [m - 1]$,$S_i := S \cap D_1$,$S_2 = S\setminus S_1$。则
$$
\Pr\left[A_m \bigg| \bigcap_{j\in S} \overline{A_j} \right] = \frac{\Pr\left[A_i\cup\bigcap_{j\in S_1}\overline{A_j}\big|\bigcap_{j\in S_2} \overline{A_j}\right]}{\Pr\left[\bigcap_{j\in S_1}\overline{A_j}\big|\bigcap_{j\in S_2} \overline{A_j}\right]}
$$
根据题目条件分子不超过 $p$。根据归纳假设
$$
\Pr\left[\bigcap_{j\in S_1}\overline{A_j}\big|\bigcap_{j\in S_2} \overline{A_j}\right] \geq \left(1 - \frac{1}{d + 1}\right)^{d} \geq \frac{1}{e}
$$
在根据题目条件这个商不超过 $ep \leq 1 / (d + 1)$。$\blacksquare$
尝试在此基础上弱化条件。发现其实上述归纳成立只需要:
定理 2(General LLL). 设 $A_1, …, A_n$ 是一系列坏事件。若存在 $x_1, …, x_n$ 使得 $\Pr[A_i] \leq x_i\prod_{j\in D_i} (1 - x_j)$ 则
$$
\Pr\left[\bigcap_{i=1}^n \overline{A_i}\right]\geq 0
$$
另外还有一个实用的版本是
定理 3(Asymmetric LLL). 坏事件的定义同上,若 $\sum_{j\in D_i} \Pr[A_j] < 1/4$ 则
$$
\Pr\left[\bigcap_{i=1}^n \overline{A_i}\right]\geq 0
$$
Remark. 其实更松的界是 $\frac 12\ln 2$,证明是令 $x_i = 2\Pr[A_i]$,然后验证在此条件下 General LLL 的条件成立。
以下是一些应用:
数据包路由. 考虑一张无向图 $G$,第 $i$ 个数据包沿着路径 $P_i$ 传输,每条边的容量是 $1$(单位时间只能通过一个包)。定义 $c_e$ 为 $P_i$ 的长度,$c = \max{c_e}$,$d$ 为包的数量。则最优决策下,传输完成时间几何?
显然 $T = \Omega(c + d)$。我们将证明 $T = O((c + d)2^{O(\log^*(c + d))})$。(这基本上是 $O(c + d)$,因为 $\log^*$ 增长非常慢。最好的结果是 $O(c + d)$,但是我不会。)
$\color{red}{\text{Sorry.}}$
图的 Frugal 着色. 称 $G$ 的一个合法着色(相邻点不同色)是 $\beta$-frugal 的,若对于任何 $v$,其邻居中没有任何一种颜色出现了 $\beta$ 次。
兹证明最大度数 $\Delta \geq \beta^\beta$,则 $G$ 有一种 $16\Delta^{1 + 1/\beta}$ 色的 $\beta$-frugal 着色。
Probabilistic method,随机染色,考察两种坏事件:
- $A_{u, v}$ 表示 $u, v$ 同色;
- $B_{v_1, …, v_{\beta + 1}}$ 某个点的一众邻居同色。
计算发现它确实满足 Asymmetric LLL 的条件,很 trivial 所以不写。
无偏估计
定义 1(FPRAS). 一个 FPRAS(fully polynomial randomized approximation scheme),顾名思义,系指一个多项式时间($\mathrm{poly}(n, 1/\varepsilon, 1 / \delta)$)生成结果的乘性近似估计(高概率有估计值满足 $((1 - \varepsilon) x \leq \hat{x} \leq (1 + \varepsilon) x)$)的随机算法。
首先来分析无偏估计的精度强化问题。
定理(Median Trick). 给定 $\varepsilon, \delta > 0$,和 $\mu$ 的无偏估计 $X$。设 $\mathrm{Var}[X] = \sigma^2$。则可通过
$$
T = O\left(\left(\frac{\sigma}{\mu}\right)^2\frac{1}{\varepsilon^2}\log\frac{1}{\delta}\right)
$$
个样本 $X_1, …, X_T$ 构造 $\mu$ 的一个估计 $\hat{X}$ 使得
$$
\Pr\left[|\hat{X}| - \mu \geq \varepsilon \mu\right] \leq \delta
$$
证明. 从这个式子你也能看出来这个无偏估计是怎么做的:
- 令 $t = \left(\frac{\sigma}{\mu}\right)^2\frac{1}{\varepsilon^2}$,重复 $t$ 次实验取均值可得到常数概率 $1\pm \varepsilon$ 近似(切比雪夫不等式)。
- 重复 $1$ 步骤 $\log 1 / \delta$ 次,取结果的中位数,结果是 $1\pm \varepsilon$ 近似的概率可强化至 $1 - \delta$(Chernoff bound)。
$\blacksquare$
接下来是几个例子。
Buffon’s Needle. 通过在两两间距为 $1$ 的平行线上投一根长度为 $1$ 的针,统计针与线相交的次数可以无偏估计 $\pi$。
因为过于经典,所以不再赘述。
此例子代表了构造 Monte-Carlo 估计的要旨:
- 构造一个全集 $U$,向其中嵌入一个子集 $S\subseteq U$,使得欲无偏估计的量正好是 $|S| / |U|$;
- 在 $U$ 上均匀采样,统计 $x\in S$ 的概率。
并集大小估计. 给定一些集合 $A_1, …, A_n$,估计 $|A_1\cup\cdots\cup A_n|$ 的大小。
这里 $A_i$ 可能是隐式给出的(大小可以非常大),但是容易从中均匀采样、容易计算大小。
因为 $\sum_{i=1}^n |A_i|$ 是容易计算的,我们如此构造全集 $U$ 并向其中嵌入一个大小等于 $|A_1\cup\cdots\cup A_n|$ 的子集 $S$:
- 令 $A_i^+ = \{(x, i) : x\in A_i\}$。全集 $U := \cup_{i=1}^n A_i^+$;
- 令子集 $S := \{(x, i) : i = \min\{j : x\in A_j\}\}$。容易证明其大小恰为 $|A_1\cup\cdots\cup A_n|$。
考虑如何从 $U$ 中均匀采样。显然,我们只需要以正比于集合大小的概率先选择 $i$,再从 $A_i$ 中均匀采样 $x$。显然能够快速判断采出的样本是否属于 $S$。
因此,我们得到了
$$
\frac{\left[\cup_{i=1}^n A_i\right]}{\sum_{i=1}^n |A_i|}
$$
的一个无偏估计,将其乘上 $\sum_{i=1}^n |A_i|$ 便得原问题的无偏估计。
因为答案足够大,所以可以用 Median Trick 证明存在 FPRAS。
Remark. 这个例子的应用是给出 $\#\mathrm{DNF}$ 的一个无偏估计。$\#\mathrm{DNF}$ 是一个经典的 $\#\mathbf{P}\text{-complete}$ 问题,其内容为数有多少组赋值能满足一个析取范式。
网络可靠性. 对于一张图 $G$,其 $p$-可靠性定义为其 $p$-渗滤(即以 $p$ 概率保留每条边)连通的概率。则存在估计 $p$-可靠性的 FPRAS。
设 $c$ 为图的最小割,可以用 Stoer-Wagner 算法求出。若 $p^c \geq \frac{1}{n^4}$,则可以直接用 Monte-Carlo 无偏估计。下不妨设 $p^c$ 并不大。
接下来的直觉为问题铺平了道路:一张图的最小割不多。为此,我们仿照 Stoer-Wagner 中缩点的思路,配合随机化方法解决。对于图中的任意一个最小割 $(A, \bar{A})$,其割边集合为 $\mathcal{C}$。我们重复“随机选择一条边、缩点”的操作,直到最后仅剩两个点。注意:
断言 1. 如果没有选中 $\mathcal{C}$ 中的边,则新图的最小割仍然是 $c$。
断言 2. $\mathcal{C}$ 中的边在整个过程中未被选中的概率至少是(注意最小割为 $c$ 表明度数至少是 $c$,进而边数有下界)
$$
\prod_{i=1}^n \left(1 - \frac{c}{c\cdot (n - i + 1) / 2}\right) = \frac{2}{n(n / 2)}
$$
这给出最小割的大小至多是 $O(n^2)$。推而广之,定义 $\alpha$-最小割为大小不超过 $\alpha c$ 的割。
断言 3. $\alpha$-最小割的个数不超过 $n^{2\alpha}$。且可以在 $O(n^{2\alpha}\log n^{2\alpha})$ 时间内列出。
重复上方随机缩点的论证。只是此时在只有 $2\alpha$ 个点剩余时,我们便停止,然后随机输出此图中的一个割。可以算出,一个 $\alpha$-最小割 $\mathcal{C}$ 在删边后仍然存活,且被选出的概率至少是
$$
\prod_{i=1}^n \left(1 - \frac{\alpha c}{\alpha c\cdot (n - i + 1) / 2}\right) \cdot 2^{-2\alpha c} = \binom{n}{2\alpha}^{-1}\frac{1}{2^{\alpha c}} \geq \frac{1}{n^{2\alpha}}
$$
重复运行算法,便可如 coupon collector 一般收集全部 $\alpha$-最小割。最后解决本题的算法如下:
- 令 $\alpha = 2 + \frac 12 \log_n 2/\varepsilon$;
- 列举所有的 $\alpha$-最小割,在上方用带权 $\#\mathrm{DNF}$ 的算法估计删掉的边包含这些 $\alpha$-最小割的概率;
- 直接输出第三步的估计作为答案。
为了证明这个算法是正确的,只需证明删掉那些大割的概率和是 $o(1)$ 的,因此不影响估计即可。
$\color{red}{\text{Sorry.}}$
集中不等式
列举一些 chernoff bound 的形式。记 $X_1, …, X_n$ 是 $n$ 个独立同分布的伯努利分布($\mathrm{Bern}(p)$)。令 $X$ 为其和,和的期望为 $\mu = np$。证明路径是用矩生成函数方法算出最原始的那个 Additive Chernoff Bound,然后别的基本上都是用一些小微积分来放缩 KL 散度。
Additive Chernoff Bound.
$$
\begin{aligned}
\Pr\left[X \geq \mu + \lambda\right] &\leq \exp\left(-nD_{KL}(p + \lambda / n \Vert p)\right) \\
\Pr\left[X \leq \mu - \lambda\right] &\leq \exp\left(-nD_{KL}(1 - p + \lambda / n \Vert 1 - p)\right)
\end{aligned}
$$
根据 KL 散度的凸性可知
$$
\begin{aligned}
\Pr\left[X \geq \mu + \lambda\right] &\leq \exp\left(-2\lambda^2 / n\right) \\
\Pr\left[X \leq \mu - \lambda\right] &\leq \exp\left(-2\lambda^2 / n)\right)
\end{aligned}
$$
Multicative Chernoff Bound. 对于任意的 $\beta\in (0, 1)$ 有
$$
\begin{aligned}
\Pr\left[X \leq (1 - \beta)\mu\right] \leq \exp\left(-\frac{\beta^2\mu}{2}\right) \\
\Pr\left[X \geq (1 + \beta)\mu\right] \leq \exp\left(-\frac{\beta^2\mu}{2 + \beta}\right)
\end{aligned}
$$
首先是一些集中不等式的趣味小应用。
随机网络路由. 考虑一个 $n$ 维立方体 $\{0, 1\}^n$(两个点有连边当且仅当其汉明矩为 $1$),每条边有 $1$ 的双向容量。对于任意一个排列 $\pi$ 表示 $i$ 要去 $\pi(i)$。规划一个路由方案来最小化移动完成的时间。
存在一个算法,高概率在 $O(n)$ 时间内完成。
考虑如下的随机中转方案:先独立随机采样一个 $\delta \in [1, n]$,让每个 $i$ 先去 $\delta(i)$,然后从 $\delta(i)$ 去 $\pi(i)$。移动方式都是直接走 bit fixing 最短路(从左到右修改不一样的位),如果被堵住了就等待。
设 $D(i)$ 表示 $i$ 等待的时间,$S(i)$ 表示路径与其他点的路径相交的次数。可以断言 $D(i) \leq S(i)$。
证明. $\color{red}{\text{Sorry.}}$(“甩锅”法)
接下来只需要给出 $S(i)$ 的指数级收敛性即可。即 $\Pr[S(i) \geq cn] \leq \exp(-2n)$。、
证明. 定义 $H_{ij}$ 表示路径 $i, j$ 是否相交。显然,这是一众独立的伯努利分布随机变量。$S(i) = \sum_{j \ne i} H_{ij}$。对于每条边,期望经过它的路径条数为
$$
\begin{aligned}
&\frac{2^n\cdot n / 2}{2^n\cdot n} = \frac 12 & \color{blue}{\frac{\text{$\#$ of covered edges}}{\text{$\#$ of total edges}}}
\end{aligned}
$$
因此 $\mathbb{E}[S(i)] \leq n/2$。根据 multicative Chernoff bound:
$$
\Pr[X\geq (1 + \beta)\mu] \leq \exp\left(-\frac{\beta^2}{2 + \beta}\mu\right)
$$
可以证明 $(1 + \beta)\mu$ 固定时,$\mu$ 越大 bound 越紧,因此取 $\beta = 6$ 可以得到一个 $\exp\left(-2n\right)$ 的 upper bound。$\blacksquare$
The Power of Two Choices
Remark. 本节将揭示往往只需要一些简单的随机选择便可能实现效果良好的负载均衡。为此,我们先分析最简单的随机方法下高概率的最大负载,然后分析每次选择两个桶,然后向较负载较小的桶中加一个球高概率的最大负载。
考虑如下情景:向 $n$ 个桶中随机投放 $m$ 个小球(每个小球的投放位置从 $n$ 个桶中均匀随机抽取)。我们现在想要分析诸桶的最大负载(i.e. 球最多的桶里面有多少球)。首先需要明确的是,球的状态服从多项分布,即
$$
\Pr[X_1 = k_1, …, X_n = k_n] = \frac{1}{n^m}\frac{m!}{k_1!…k_n!}
$$
其中 $\sum_{i=1}^n k_i = m$。因为 $X_i$ 之间并不独立,所以分析难以进行,但是注意到,令 $Y_1, …, Y_n$ 是 $n$ 个独立服从泊松分布 $\pi(m / n)$ 的随机变量,则不难验证
$$
\Pr[X_1 = k_1, …, X_n = k_n] = \Pr\left[Y_1 = k_1, …, Y_n = k_n \bigg | \sum_{i=1}^n Y_i = m\right]
$$
下面的定理揭示了多项分布下的事件发生的概率可以用泊松分布近似。
定理 1. 令 $\mathcal{E}$ 是一个仅基于桶的负载的事件,满足 $\Pr[\mathcal{E}]$ 关于 $m$ 单调递增(或递减),则
$$
\Pr_X[\mathcal{E}] \leq 4\Pr_Y[\mathcal{E}]
$$
其中 $\Pr_X$ 为将 $X$ 视作桶的负载时对应的概率,$\Pr_Y$ 类似;可以发现,后者取消了球的总数,并让每个桶中的球数独立。
证明. 这里只证明递增的情况,递减的情况时完全类似的。有
$$
\begin{aligned}
\Pr_Y[\mathcal{E}] &= \sum_{k=0}^\infty \Pr_Y\left[\mathcal{E} \bigg| \sum Y_i = k\right]\Pr_Y\left[\sum Y_i = k\right] \\
&\geq \Pr_Y\left[\mathcal{E} \bigg|\sum Y_i = m\right]\Pr_Y\left[\sum Y_i \geq m\right] \\
&\geq \frac 14\Pr_X[\mathcal{E}]
\end{aligned}
$$
此处的常数 $1/4$ 来源于关于泊松分布的简单事实 $\Pr[Y\geq \mathbb{E}[Y]] \geq 1/4$;至少在 $m = n$ 的时候这个是对的。
接下来我们形式化“最大负载”:
定理 2. 对于上述的球和桶模型,有高概率最大负载是 $\Theta(\ln n / \ln \ln n)$ 的。
证明. 令 $\varepsilon > 0$,定义 $c_1 = 1 + \varepsilon, c_2 = 1 - \varepsilon$。只需要证明:
- 小概率存在一个桶中球的数量 $> c_1\ln n / \ln \ln n$,记作事件 $\mathcal{E}_1$;
- 小概率所有桶中球的数量 $< c_2 \ln n / \ln \ln n$,记作事件 $\mathcal{E}_2$。
首先可以考察一下泊松分布 $\pi(1)$ 的尾部,令 $p_k = \sum_{j = k}^\infty \frac{e^{-1}}{j!}$,显然
$$
\frac{1}{ek!}\leq p_k \leq \frac{1}{k!}\cdot \frac 1e\left(1 + \sum_{i=1}^n \frac{1}{(k+1)^{\overline i}}\right) \leq \frac{1}{k!}
$$
接下来,注意上述事件都符合定理 $1$ 的要求。取 $k = (1 + \varepsilon)\ln n/\ln\ln n$,则证明第一个断言只需要应用一次 Union Bound:
$$
\begin{aligned}
\Pr[{\mathcal{E}_1}]
\leq n p_k
\leq n\exp(-\ln k!)
\approx n\exp(-k\ln k)
\approx n\exp(-(1 + \varepsilon)\ln n)
= o(1)
\end{aligned}
$$
且使用定理 $1$ 以后,我们取消了桶之间的非独立性,因此证明第二个断言时可以直接将概率拆成乘积:
$$
\Pr_Y[{\mathcal{E}_2}] = (1 - p_k)^n \leq \left(1 - \frac{1}{ek!}\right)^{n} \leq e^{-\frac{n}{ek!}} \approx \exp\left(-\frac{n}{e\exp((1-\varepsilon)n)}\right) = o(1)
$$
接下来考察另一种情形,每次选择两个桶,然后向较负载较小的桶中加一个球。我们将证明这样操作使得最大负载高概率是
$$
\frac{\ln \ln n}{\ln 2} + \Theta(1)
$$
和上方的结果做对比可以发现这样使得最大负载指数级地下降。这称为 The Power of Two Choices。
$\color{red}{\text{Sorry.}}$
随机图哈密尔顿回路
随机图 $\mathcal{G}_{n, p}$ 是一个随机变量,它是一个 $n$ 个点的图,图中每条边出现的概率为 $p$。
存在一个多项式算法,高概率成功找到 $G$ 的一个哈密尔顿回路,其中 $G$ 服从分布 $\mathcal{G}_{n, p}$,$p\geq \frac{72\ln n}{n - 1}$
该算法很像 OI 圈知名的 dls 调整法。需要先对图进行一些调整,然后可以用 coupon collector 分析。
$\color{red}{\text{Sorry.}}$
分支过程
本节重点证明随机图上,关于图中最大的连通块有如下的阈值:
定理 1. 考虑随机图 $G = \mathcal{G}_{n, p}$,其中 $p = \frac{c}{n}$,此处 $c$ 是常数。我们有:
- 若 $c < 1$,则 $G$ 中最大连通块大小为 $O(\log n)$,a.a.s.
- 若 $c > 1$,则 $G$ 中存在一个大小为 $\beta n(1 + o(1))$ 大的连通块,其中 $\beta$ 是 $\beta + e^{-\beta c} = 1$ 在 $(0, 1)$ 上的解;进一步,次大连通块大小为 $O(\log n)$,a.a.s.
上述表述中,「a.a.s」为 asymptotically almost surely 的缩写,系指当 $n\rightarrow \infty$ 时事件发生的概率趋近于 $1$。
首先,我们需要建立一些关于上述定理中所述的奇怪的方程 $\beta + e^{-\beta c} = 1$ 的直觉。这个方程源自 Galton-Watson 分支过程,其相关定义如下:
定义 1(Galton-Watson 分支过程). 设 $X$ 是一非负整数随机变量,则由 $X$ 定义的分支过程起始于一个单独的节点;每个时间步,上一个时间步新产生的每个节点将产生 $X$ 个儿子。
用随机变量 $Z_i$ 刻画第 $i$ 个时间步时产生的节点数量,依定义有 $Z_0 = 1$。定义事件“灭绝(extinction)”为在该分支过程中,最终某一层不产生任何儿子,形式化地:
$$
\Pr[\text{extinction}] = \lim_{n\rightarrow \infty}\Pr[Z_n = 0]
$$
这个模型类似于传染病传染的过程。$X$ 的期望值 $\mathbb{E}[X]$ 正是传染病中的 $R_0$ 的一种更为通用的刻画。我们有:
定理 2. 对于一个由 $X$ 定义的分支过程,若 $\Pr[X = 0] > 0, \Pr[X = 1] < 1$,则
- 若 $\mathbb{E}[X]\leq 1$,则 $\lim_{n\rightarrow\infty} \Pr[Z_n = 0] = 1$,即该过程将灭绝,a.a.s.
- 若 $\mathbb{E}[X] > 1$,则 $\lim_{n\rightarrow \infty}\Pr[Z_n = 0] = p^* < 1$,其中 $p^*$ 时 $f(x) = x$ 在 $(0, 1)$ 之间的唯一解($f(x)$ 为 $X$ 的概率生成函数)。
证明. 记 $f_n$ 为 $Z_n$ 的概率生成函数,即
$$
f_n(x) := \sum_{i\geq 0} \Pr[Z_n = i]x^i
$$
注意到 $f_n$ 满足如下递推关系:$f_n(x) = f(f_{n - 1}(x))$。现在要分析的是 $\Pr[Z_n = 0]$,即 $q_n := f_n(0)$。直接向上述递推关系中代入 $x = 0$ 得到 $q_n$ 满足如下递推关系:$q_n = f(q_{n - 1})$。不难收集如下关于 $f(x)$ 和 $q_n$ 的性质:
- $q_n$ 单调递增(因为如果前一时刻已经灭绝,那么以后必然也灭绝)且有界(概率不超过 $1$),因此必然收敛。
- $f(x)$ 为 $[0, 1]$ 上的连续单调递增下凸函数。
以上两条联合起来给出 $q$ 的极限是 $f(x)$ 在 $[0, 1]$ 上的不动点。注意 $f(1) = 1$,因此 $f(x) = x$ 在 $(0, 1)$ 有解当且仅当 $\mathbb{E}[X] = f’(1) > 1$。在证明过程中我们省略了一些琐碎的数学分析,然而可以参照下面的图像理解此证明:
在随机图上,我们可以通过 bfs 来遍历一个连通块,即每次揭示一排点的邻居。这和 Galton-Watson 分支过程如出一辙。注意,一个点的邻居数量几乎就是服从二项分布 $B(n, c/n)$。当 $n$ 趋向无穷大时,这个分布点点收敛于泊松分布 $\pi(c)$。而泊松分布的生成函数是
$$
f(x) = \sum_i\frac{c^ie^{-c}}{i!}x^i = e^{c(x - 1)}
$$
所以 bfs 停下的概率 $p^*$ 是方程
$$
e^{c(x - 1)} = x
$$
的整数解。$\beta = 1 - x$ 可以视为一个点在最大连通块中的概率,这样便得到了定理 1 中的方程 $\beta + e^{-\beta c} = 1$。
最后来严格证明一次本节定理 1。
第一部分($c < 1$ 时最大连通块不大). 考虑事件“一个点 $v$ 在一个大小为 $k$ 的连通块中”的概率。此事件发生仅当一个 bfs 状的分支过程至少产生了 $k$ 个节点,且所有节点产生的儿子总数超过 $k - 1$,即
$$
\sum_{i=1}^k X_i \geq k - 1, \text{where $X_i \sim B\left(n - \sum_{j = 1}^{i - 1}X_j, c/n\right)$}
$$
这个事件看起来难以分析,但是可以注意到将 $X_i$ 的分布宽限为 $B(n, c/n)$,得到的概率定不会变小。即
$$
\begin{aligned}
\Pr[\text{$v$ in a component of size $\geq k$}] &\leq \Pr\left[\sum_{i=1}^l X_i\geq k - 1\right] \text{where $X_i\sim B(n, c/n)$, i.i.d.} \\
&=\Pr\left[\sum_{i=1}^k X_i - ck \geq (1-c)k - 1\right] \\
&\leq \exp\left(-\frac{((1 - c)k - 1)^2}{ck^2(2 + ((1-c)k - 1)/ck)}ck\right) \\
&=\exp\left(-\frac{(1-c)^2 k}{2} + O(1)\right)
\end{aligned}
$$
Hint.
这里第三行是一个 Chernoff bound,回忆
$$
\Pr[X\geq (1 + \delta)\mu] \leq \exp\left(-\frac{\delta^2 \mu}{(2 + \delta)}\right)
$$
在本推导中 $\delta = \frac{(1 - c)k - 1}{ck}$,$\mu = ck$。
取 $k = \frac{3}{(1 - c)^2}\ln n$,上述概率不超过 $O(n^{-\frac{3}{2}})$,对所有点用 union bound 得到存在一个连通块大小超过 $3\ln n/(1-c)^2$ 的概率仅为 $o(1)$ 级别。
第二部分($c > 1$ 时只有一个大连通块). $\color{red}{\text{Sorry.}}$
鞅
本节讲随机过程中的重要概念鞅,主要围绕其集中不等式和可选停时定理展开。
定义 1(鞅). 给定一列非降 $\sigma$-代数 $\varnothing = \mathcal{F}_0 \subseteq \mathcal{F}_1 \subseteq \mathcal{F}_n$,称作滤子(filter),以及一列随机变量 $X_1, …, X_n$。若对于任意的 $i$ 都有 $\mathbb{E}[X_i | \mathcal{F}_{i - 1}] = X_{i - 1}$($\star$),则 $(X_i)$ 称作关于 $(\mathcal{F}_i)$ 的鞅;$Y_i = X_i - X_{i - 1}$ 称作其差分序列,依定义有 $\mathbb{E}[Y_i | \mathcal{F}_i] = 0$。
有一些鞅的变种。如果将($\star$)修改作 $\mathbb{E}[X_i | \mathcal{F}_{i - 1}] \geq \mathbb{X}_{i - 1}$ 则称为下鞅(submartingale),若修改作 $\mathbb{E}[X_i | \mathcal{F}_{i - 1}] \leq \mathbb{X}_{i - 1}$ 则称为上鞅(supermartingale)。
一个常举的例子是有一个点 $x$ 在数轴上随机游走,每时刻其坐标等概率地 $+1$ 或者 $-1$,$n$ 步之后停止。那么显然,该点最终位置的期望值是关于前 $i$ 次移动方向的鞅。当然在 CS 中,我们通常不需要用到非降 $\sigma$-代数这种抽象层级的概念,只需采纳一种形象的理解,即鞅是在一个逐渐发展的过程中,随着新信息被不断揭露,对结果的估计量。因此可将那一列非降 $\sigma$-代数替换做一列随机变量 $Z_1, …, Z_n$,并将定义对应修改为 $\mathbb{E}[X_i | Z_{1}…Z_{i - 1}] = X_{i - 1}$。
对于任意一个随机变量 $A$ 和一列随机变量 $Z_1, …, Z_n$,我们都可以构造一个鞅。
定理 1(Doob 鞅). 令 $A$ 和 $Z_1, …, Z_n$ 为同一个概率空间上的随机变量。则 $X_i = \mathbb{E}[A | Z_1 … Z_i]$ 是一个鞅,称作 $A$ 的 Doob 鞅。
证明.
只需要验证即可,注意(第二行只需按定义计算即可)
$$
\begin{aligned}
\mathbb{E}[X_i | Z_1 … Z_{i - 1}] &= \mathbb{E}[\mathbb{E}[A | Z_1 … Z_i] | Z_1 … Z_{i - 1}] \\
&= \mathbb{E}[A | Z_1 … Z_{i - 1}]
\end{aligned}
$$
Azuma 不等式
直觉上如果一个随机过程是一个鞅过程,那么它最后的结果应该会比较集中。这个集中不等式的证明是一个标准的矩生成函数法,先证明 Hoeffding Lemma(的一个弱化版)
引理 2(Hoeffding Lemma). 对于随机变量 $X$,若 $|X| \leq c, \mathbb{E}[X] = 0$,则 $\mathbb{E}[e^{tX}] \leq e^{(ct)^2 / 2}$。
证明. 只需要证明 $c = 1$ 的情况,其余可以通过缩放来推广。
根据 $e^x$ 的凸性有 $\mathbb{E}[e^{tX}] \leq \frac 12(e^t + e^{-t})$,将右侧泰勒展开后奇数项全消掉了,可以发现它等于 $e^{t^2 / 2}$。$\blacksquare$
定理 3(Azuma 不等式). 若 $(X_i)$ 是关于 $(\mathcal{F}_i)$ 的鞅,且 $(X_i)$ 的差分序列 $(Y_i)$ 满足 $|Y_i| \leq c_i$,则
$$
\begin{align}
\Pr[X_n \geq X_0 + \lambda] \leq \exp\left(-\frac{\lambda^2}{2\sum_{i=1}^n c_i^2}\right) \\
\Pr[X_n \geq X_0 - \lambda] \leq \exp\left(-\frac{\lambda^2}{2\sum_{i=1}^n c_i^2}\right)
\end{align}
$$
证明. 只用证上面半边。考虑马尔可夫不等式
$$
\begin{aligned}
\Pr\left[e^{t(X_n - X_0)} \geq e^{t\lambda}\right] &\leq e^{-t\lambda}\mathbb{E}[e^{t(X_n - X_0)}] \\
&= e^{-t\lambda}\mathbb{E}[\mathbb{E}[e^{t(Y_n + X_{n - 1} - X_0)}|\mathcal{F}_{n - 1}]] \\
&= e^{-t\lambda}\mathbb{E}[e^{t(X_{n - 1} - X_0)} \cdot {\color{blue}\mathbb{E}[e^{tY_n} | \mathcal{F}_{n - 1}]}]
\end{aligned}
$$
至此已经形成明显的递归结构,根据 $Y_i$ 的条件和鞅的性质,蓝色部分符合 Hoeffding Lemma 的使用条件,因此归纳可知
$$
\Pr\left[e^{t(X_n - X_0)} \geq e^{t\lambda}\right] \leq \exp\left(\frac {t^2}2\sum_{i=1}^n c_i^2 - \lambda t\right) \leq \exp\left(-\frac{\lambda^2}{2\sum_{i=1}^n c_i^2}\right)
$$
下半边取相反数可得证。$\blacksquare$
定理 4(Doob 鞅上的 Azuma 不等式). 设 $f$ 是关于随机变量 $Z_1, …, Z_n$ 的 $n$ 元 $c$-Lipschitz 函数(i.e. 改变 $f$ 的一个坐标值,函数变化不超过 $\pm c$),若 $Z_i$ 在 $Z_1, …, Z_{i - 1}$ 的条件下和 $Z_{i + 1}, …, Z_n$ 独立($\star$),则 $X_1, …, X_n$ 为 $f$ 关于 $(Z_i)$ 的 Doob 鞅,则
$$
|X_i - X_{i - 1}| \leq c
$$
进而满足 Azuma 不等式。
证明. 道理很简单,实际写起来有点繁琐,本质上就是一个 dummy variable 换元。 记 $\hat{Z}_i$ 是在 $Z_1, …, Z_{i - 1}$ 条件下同 $Z_i$ 独立同分布的一个东西,它和 $Z_i, Z_{i + 1}, …, Z_n$ 独立。则
$$
\begin{aligned}
X_{i - 1} &= \mathbb{E}_{Z_i, …, Z_n}[f | Z_1, …, Z_{i - 1}] \\
&= \mathbb{E}_{Z_{i + 1}, …, Z_n}[\mathbb{E}_{Z_i}[f | Z_1, …, Z_{i - 1}, Z_{i + 1}, …, Z_n] | Z_1, …, Z_{i - 1}] & \color{blue}{\text{(chain rule)}} \\
&= \mathbb{E}_{\hat{Z}_i, Z_{i + 1}, …, Z_n}[f(…, \hat{Z}_i, …) | Z_1, …, Z_{i - 1}] & \color{blue}{\text{(definition of $\hat{Z}_i$)}} \\
&= \mathbb{E}_{\hat{Z}_i, Z_{i + 1}, …, Z_n}[f(…, \hat{Z}_i, …) | Z_1, …, Z_{i - 1}, Z_i] & \color{blue}{\text{(independentness)}}
\end{aligned}
$$
因此
$$
\begin{aligned}
&\mathbb{E}[f | Z_1, …, Z_i] - \mathbb{E}[f | Z_1, …, Z_{i - 1}] \\
&= \mathbb{E}[f(…, Z_i, …) - f(…, \hat{Z}_i, …) | Z_1, …, Z_i] \\
&\leq c
\end{aligned}
$$
$\blacksquare$
实际上,我们在绝大多数算法问题(尤其是 conditional probabilistic method)中遇到的都是这样的 $c$-Lipschitz 函数(问题的可行解 $\rightarrow$ 解的价值)的 Doob 鞅。下面是一些应用。
球和桶. 向 $n$ 个桶中随机丢 $m$ 个球,空桶个数的集中性如何?
$f(x_1, …, x_m)$ 表示第 $i$ 个球丢进了第 $x_i$ 个桶时的空桶个数,是 $1$-Lipschitz 函数,因此有
$$
\Pr[|X - \mathbb{E}[X]| > \lambda] \leq e^{-\lambda^2 / 2m}
$$
Chernoff bound 难以给出这样的界,因为每次丢球后空桶个数的减少量不太独立。
随机图色数. $\chi(\mathcal{G}_{n, 1/2})$ 的集中性如何?
关于随机图,有两个常见的鞅
- Vertex exposure 鞅. $Z_i$ 表示 $i$ 和 $1, …, i - 1$ 的连边情况。
- Edge exposure 鞅. $Z_i$ 表示第 $i$ 条边是否存在。
函数 $f$ 表示对应连边情况的色数。注意到,无论是在 vertex exposure 鞅还是 edge exposure 鞅的滤子上,$f$ 都是 $1$-Lipschitz(把涉及到的点改成一个没出现过的颜色总能满足染色条件),得到的集中不等式为
$$
\Pr[|X - \mathbb{E}[X]| > \lambda] \leq e^{-\lambda^2 / 2n} \quad \text{or} \quad {\color{lightgray} \Pr[|X - \mathbb{E}[X]| > \lambda] \leq e^{-\lambda^2 / 2m}}
$$
前者更紧。
快速排序(Hayward,McDiarmid 96). 随机快排的集中性如何?
熟知随机快排的期望复杂度是
$$
q_n = 2n\ln n - (4 - 2\gamma)n + 2\ln n + O(1)
$$
本小节证明对于任意的 $\varepsilon > 0$(这篇文章甚至证出了这个界是紧的,那很厉害了)
$$
\Pr[|Q_n - q_n| > \varepsilon q_n] \leq n^{-(2 + o(1))\varepsilon \ln\ln n}
$$
$\color{red}{\text{Sorry.}}$
可选停时定理
定义 2(停时). $(\mathcal{F}_i)$ 是滤子,一个随机变量 $T \in \mathbb{N}\cup\{\infty\}$ 是 $(\mathcal{F}_i)$ 的一个停时当且仅当任意的事件 $T = i$ 都是 $\mathcal{F}_i$-可测的。
Remark. 这就是说你总能从当前的局面判断要不要停。
定理 5(可选停时定理). $(X_i)$ 是 $(\mathcal{F}_i)$ 上的鞅,$T$ 是停时,则若以下条件成立,则 $\mathbb{E}[X_T] = \mathbb{E}[X_0]$:
- $\Pr[T < \infty] = 1$;
- $\mathbb{E}[X_T] < \infty$;
- $\mathbb{E}[X_i \mathbf{1}\{T > i\}]\rightarrow 0 (i\rightarrow \infty)$。
这组条件可以被换成一组更弱的条件比如
- $\mathbb{E}[T] < \infty$;
- $\mathbb{E}[|X_i - X_{i - 1}| \mid \mathcal{F}_i] < c$。
另外,对应条件下,在下鞅上可以证出 $\mathbb{E}[X_T] \geq \mathbb{E}[X_0]$,在上鞅上可以证出 $\mathbb{E}[X_T]\leq \mathbb{E}[X_0]$。
证明. $\color{red} \text{Sorry.}$
注意停时定理是关于停止时的 $X_T$ 的结论,而不是关于 $T$ 的结论。为了得到关于 $X_T$ 的结论,经典的办法是在鞅上面再造一个鞅。
断言 6. 若 $(X_i)$ 是一个鞅,$D_i$ 是其差分序列。若 $\mathbb{E}[D_i^2 | \mathcal{F}_{i - 1}] = \sigma^2$,则 $Y_i = X_i^2 - \sigma^2 i$ 是也一个鞅。
若 $(X_i)$ 是一个上鞅,其值域为 $[0, n]$,$D_i$ 是其差分序列,若 $\mathbb{E}[D_i^2 | \mathcal{F}_{i - 1}] \geq \sigma^2$,则 $Y_i = X_i^2 - 2n X_i - \sigma^2 i$ 是一个下鞅。
证明. 验证即可。系数配比的关键是:首先要配一个和 $i$ 相关的东西进去,然后再调整一点别的东西让它能继续保持鞅的性质。$\blacksquare$
这样一来,如果有一个鞅,我们就知道 $\mathbb{E}[T] = \mathbb{E}[X_T^2]$;如果有一个 $[0, n]$ 上的上鞅(你的算法让某个量期望意义下减少),且停时为 $T : X_T = 0$(减到 $0$ 就停止),就可以知道 $\mathbb{E}[T] \leq \mathbb{E}\left[\frac{2nX_0 - X_0^2}{\sigma^2}\right] \leq n^2 / \sigma^2$
以下是一些应用。
赌徒之殇. 一个赌徒初始时持有 $a$ 元本金进场,每次等概率赢得 $1$ 元或输掉 $1$ 元,当其输光本金或得利 $b$ 元时离场,问其离场时期望得利几何?破产概率几何?期望离场时间几何?
设其 $i$ 时间得利为 $X_i$ 元。显然,$(X_i)$ 是关于每轮结果的鞅,可以验证 $\mathbb{E}[T] < \infty$,因此符合停时定理的使用条件。
Remark. 这里有点唐,为了验证这些条件你都能把 $\mathbb{E}[T]$ 算出来了,但这只是一个展示停时定理的 toy example,所以无需多虑。
根据停时定理,其离场时期望得利 $0$ 元,因此可以解出破产概率是 $b / (a + b)$。
为了求期望离场时间,再构造如下随机变量:$Y_i = X_{i}^2 - i$。容易验证 $(Y_i)$ 也是一个鞅,因此根据停时定理
$$
\mathbb{E}[T] = \mathbb{E}[X_T^2 - Y_T] = \mathbb{E}[X_T^2] - \mathbb{E}[Y_0] = ab
$$
投票选举. 现有 Alice 和 Bob 两人参加某一选举。Alice 得票 $a$ 张,Bob 得票 $b$ 张($a > b$)。假设计票时,所有选票被随机地收到,问计票过程中 Alice 票数始终领先的概率。
设 $S_i$ 表示 $i$ 时刻 Alice 领先的票数。则根据超几何分布的性质,$\frac{(a - b)}{a + b}i$ 是 $S_i$ 的一个无偏估计。受此启发我们定义一列随机变量
$$
X_i := \frac{S_{n - i}}{n - i}
$$
特别地,$X_n = 1$。则可以验证 $(X_i)$ 是鞅,$T := \{X_i = 0 \wedge X_{j} \ne 0 \quad, \forall j\ne i\}$(领先优势首次消失)是其上的停时。停止时,要么是因为过程结束($X_T = 1$),要么是因为领先优势消失($X_T = 0$),根据停时定理
$$
p = \mathbb{E}[X_T] = \mathbb{E}[X_0] = \frac{a - b}{a + b}
$$
随机游走 $2\text{-SAT}$. 有一个经典的 $2\text{-SAT}$ 的随机算法。我们首先给 $\phi$ 找一组随机赋值 $a_0$,如果这组赋值不能满足 $\phi$,则随机找一个没有满足的子句,然后随机翻转其中的一个变元。问迭代多少轮可保高概率成功?
若 $\text{2-SAT}$ 可满足,那么存在一个满足它的赋值 $a^*$。将 $X_i$ 定义做第 $i$ 次迭代后 $a^*$ 和 $a_i$ 的汉明距。注意到 $(X_i)$ 是一个上鞅,且 $\mathbb{E}[D_i^2 | \mathcal{F}_{i - 1}] = 1$,因此 $X_i^2 - 2nX_i - i$ 是一个下鞅,这给出 $T$ 的上界是 $n^2$。
$O(n^2)$ 次随机可保高概率成功。
正则图最大连通块. 定义图 $G$ 的一个 $p$-渗滤为独立地以概率 $p$ 加入其每条边得到的随机图。则令 $C_1$ 是 $d$-正则图的 $p$-渗滤的最大连通块,存在常数 $\alpha$ 使得
$$
\Pr[|C_1| \geq An^{2/3}] \leq \frac{\alpha}{A^{3/2}}
$$
对于这种题显然是考虑一个 Galton-Watson 分支过程(这会 stochastically dominate 连通块大小)。定义随机变量
$$
X_t = X_{t - 1} - 1 + B\left(d - 1, \frac{1}{d - 1}\right)
$$
显然 $X_t$ 是鞅。为了利用鞅相关工具,我们首先设计如下停时 $T := \{\min_t X_t = 0 \vee X_t > h\}$。即,前沿太大时我们也将强行掐断 bfs。那么,根节点所在连通块非常大($\mathcal{C}(r) \geq k$)这件事情包含于以下两事件的或:
- $X_T \geq h$(dfs 被掐断)
- $T \geq k$(dfs 没有终止)
兹断言, 在以下两条件成立时:
- $\mathbb{E}[(X_i - X_{i - 1})^2 | \mathcal{F}_{i - 1}]\geq \sigma^2$(过程波动更大,更有希望停止);
- $\mathbb{E}[X_T^2 | X_T \geq h] \leq Dh^2$(如果最后停止是 bfs 被掐断,希望前沿不要太大)。
有
$$
\Pr[T\geq k \cup X_T \geq h] \leq \frac 1h + \frac{Dh}{k\sigma^2} \label{percolation-claim}
$$
证明.
无论是直接用停时定理还是配合 Markov 不等式都容易证明
$$
\Pr[X_T \geq h] \leq \frac{\mathbb{E}[X_T]}{h} = \frac{1}{h}
$$
该断言显然成立,因为可以构造下鞅 $Y_i = X_i^2 - \sigma^2 i$,容易算出
$$
\mathbb{E}[T] \leq \frac{\mathbb{E}[X_T^2] - 1}{\sigma^2} \leq \frac{\frac 1h \mathbb{E}[X_T^2 | E_T\geq h]}{\sigma^2} \leq \frac{Dh}{\sigma^2}
$$
对于本题,可以算出 $\sigma^2 = \frac{d - 2}{d - 1} \geq \frac 12$,且对于充分大的 $h$ 都有
$$
\mathbb{E}[X_T^2 | X_T \geq h] \leq \mathbb{E}_{Z\sim B(d - 1, 1 / (d - 1))}[(h + z)^2] \leq h^2 + 2h + 2 \leq \frac{3}{2}h^2
$$
代入式 $(\ref{percolation-claim})$ 后令 $h = \sqrt k$ 得到对于任意 $v\in V$ 有
$$
\Pr[\mathcal{C}(v) \geq k] \leq \frac{4}{\sqrt k}
$$
注意对于连通块问题不要直接用 union bound,而是考虑
$$
\Pr[\mathcal{C}_1 \geq k] \leq \frac{\mathbb{E}[|\{v : \mathcal{C}(v) \geq k\}|]}{k} \leq \frac{4n}{k\sqrt k}
$$
取 $K = An^{2/3}$ 得到欲证的结论。$\blacksquare$
马尔可夫链
关于马尔可夫链的一众基本定义,包括马尔科夫链有唯一稳态分布的定理证明,这里都不讲。兹罗列一些众所周知的结论:
定理 1(一些基本事实). 若 $P$ 是一个不可约非周期性随机游走,则其稳态分布 $\pi$ 唯一。
若 $P$ 关于 $\pi$ 是可逆的即 $\pi(x)P(x, y) = \pi(y)P(y, x)$,则 $\pi$ 是稳态分布。
Metropolis 过程
给定一个大集合 $\Omega$ 和上面的一个不可约的连通图 $G$,和权重 $w : \Omega\rightarrow \mathbb{R}^+$,构造一个 $G$ 上的马尔可夫过程使得稳态分布恰好为 $w / Z$,其中 $Z$ 是归一化因子。
定理. 给 $G$ 的每对节点赋一个转移概率 $\kappa(x, y)$。构造如下马尔可夫链:
- 在 $x$ 处按照分布 $\kappa(x, y)$ 转移到 $y$;
- 以概率 $p = \min(1, (w(y)\kappa(y, x)) / (w(x)(\kappa(x, y))))$ 接受,以概率 $1 - p$ 返回 $x$。
这个马尔科夫链的稳态分布是 $w / Z$。
证明. 验证细致平衡条件,不失一般性设 $w(x) > w(y)$,$x, y$ 之间有边。
$$
\frac{w(x)}{Z}P(x, y) = \frac{w(x)}{Z}\kappa(x, y)\cdot \frac{w(y)\kappa(y, x)}{w(x)\kappa(x, y)} = \frac{w(y)}{Z}P(y, x)
$$
所以 $w / Z$ 毫无疑问是个稳态。$\blacksquare$
混合时间
定义 1. 对于一个不可约非周期性马尔科夫链,定义 $t$ 时间的距离为 $\Delta(t) = \max_{x\in \Omega}(\left\lVert\pi - p_x^{(t)}\right\rVert)$。这里 $\left\lVert\cdot\right\rVert$ 是统计距离($\Delta_{TV}$),$p_x^{(t)}$ 是从 $x$ 出发游走 $t$ 步的分布。
该马尔科夫链的混合时间定义为 $\tau_{\mathrm{mix}} := \min\{t : \Delta(t) < 1 / 2e\}$。
这里将混合时间定义为误差不超过 $1 / 2e$ 的时刻仅是方便起见。事实上,可以证明如下断言,进而 $\Delta(\tau_{\mathrm{mix}}\ln 1 / \varepsilon) < \varepsilon$。
命题 2. $\Delta(kt) \leq (2\Delta(t))^k$。
证明. 留待介绍了 coupling 之后。
为了介绍接下来的内容,首先介绍一些有趣的小例子。
随机插入洗牌法. 考虑如下洗牌方法:每次将最顶上的一张牌随机插入下面的牌堆,问期望多久可保证将牌洗匀?
鸽尾式洗牌法. 考虑如下问题:每次按一个二项分布 $B(n, 1/2)$ 将牌分成两堆,每次将两堆随机归并,问期望多久可保证将牌洗匀?
这里的定义非常模糊。如在随机插入洗牌法中,设 $n$ 是一个素数,则插入过程中样本空间大小为 $n^k$,永无可能产生一个 $n!$ 个元素上的均匀分布。这里有两种妥协方案:
- 牌被洗匀仅当某事件发生。求该事件发生的期望时间 / 高概率不超过多少;
- 至少洗多少次,使得分布和需要的分布相差无几。
在随机插入洗牌法中,牌被洗匀当且仅当最下面的一张牌(记作 $1$ 号牌)被拿出来插入了一次(注意到 $1$ 号牌下面的牌堆是均匀随机的)。简单计算一些几何分布的期望可知,这个事件发生的期望时间是 $O(n\log n)$。
在鸽尾式洗牌法中,考虑其逆过程,相当于每次给每张牌的权重(初始为 $0$)的二进制最高位随机加一位,然后做归并排序。因为归并排序是稳定的,所以能均匀产生所有的排列当且仅当产生的权重互不相同,因此根据生日悖论时间高概率 $2^T = O(n^2)$,可解得高概率 $T = O(\log n)$。
方案 $2$ 计算的正是混合时间,它和前者的关系是什么?为此,我们将第一种方案形式化。
定义 2(强稳定时间). 停时 $T$ 是一个强稳定时间,若 $\Pr[X_t = y | T = t] = \pi(y)$。
显然有
命题 3. 设 $T$ 是一个强稳定时间,则 $\Delta(t) \leq \Pr[T > t]$。
证明. 很显然,
$$
\Delta(t) = \mathbb{E}_T[\Delta(t)] = \Pr[T > t] \mathbb{E}[\Delta(t) | T > t] + \Pr[T \leq t] \mathbb{E}[\Delta(t) | T \leq t]
$$
注意 $\mathbb{E}[\Delta(t) | T > t] \leq 1$,$\mathbb{E}[\Delta(t) | T \leq t] = 0$。$\blacksquare$
至此,我们也可以得出随机插入洗牌法的混合时间也是 $O(n\log n)$,鸽尾式洗牌的混合时间也是 $O(\log n)$ 的结论。
接下来介绍马尔科夫链中重要的技术,coupling。引入这个技术的基本直觉如下:
- 我们现在想要 Bound $\left\lVert P_1^t - P_2^t\right\rVert$;
- 考虑从分布 $P_1$ 开始的随机游走可以产生的所有路径 $\mathcal{C}_1$ 及对应的概率,以及一个从 $P_2$ 开始的随机游走可能产生的所有路径 $\mathcal{C}_2$及对应的概率;
- 尽量将 $\mathcal{C}_1$ 和 $\mathcal{C}_2$ 中的路径配对使得每对的最后最后一步位置相同,立即得到 $\left\lVert P_1^t - P_2^t\right\rVert \leq P(\mathcal{C}_1’) + P(\mathcal{C}_2)$;
- 为了分析上的方便,我们规定配对的两条路径相等的位置要具有某些单调性。即两条路径的一个后缀都是相等的。
- 再将剩下的路径随意配对。现在整个随机过程以边缘分布为原来的分布的二元组形式呈现,这就是 coupling 的轮廓。
定义 3(coupling). 设 $(X_t), (Y_t)$ 是一个马尔科夫链的两个副本,其 coupling 为联合过程 $(X_t, Y_t)$,满足:
- 任意时间边缘分布均为原来的边缘分布(i.e. $\Pr[X_t = v] = \Pr[Y_t = v]$)。
- $X_t = Y_t \Rightarrow X_{t + 1} = Y_{t + 1}$。
停时 $T_{xy} := \min\{t : X_t = Y_t | X_0 = x, Y_0 = y\}$ 称为这个 coupling 的相遇时间。
命题 4. $\Delta(t) \leq \max_{x, y} \Pr[T_{xy} > t]$。
证明. 首先需要注意到对于任意两个随机变量 $X, Y$,有 $\Pr[X\ne Y]\geq \left\lVert P_X - P_Y\right\rVert$(可先对于伯努利分布验证这一点,然后用统计距离的等价定义)。
因此有
$$
\begin{aligned}
\max_{x, y}\Pr[T_{xy}> t] &= \max_{x, y}\Pr[X_x^t \ne X_y^t] \\
&\geq \max_{x, y} \left\lVert P_x^t - P_y^t\right\rVert \\
&\geq \max_{x} \left\lVert P_x^t - \pi\right\rVert & \color{blue}{\text{(Note that $\pi = \sum_y \pi(y) P_y^t$)}} \\
&= \Delta(t)
\end{aligned}
$$
$\blacksquare$
Remark. 根据马尔可夫不等式这自然也推出 $\tau_{\mathrm{mix}}\leq 2e\max_{x, y}\mathbb{E}[T_{xy}]$。
Remark. $\Pr[X\ne Y]\geq \left\lVert P_X - P_Y\right\rVert$ 是可以取等的。你可以对伯努利分布验证这一点,然后递归下去构造。这是我们证明下一个定理所用的重要结论。
警告. 下面的东西有可能不对,因为我还没把证明写上来。但是我确实有见过有人用这些结论,比如说北京大学 2024 Fall 离散数学与结构期末考试答案。
证明了下一个结论之后,我们就可以证明命题 $2$。这也将帮助我们理解 coupling 方法。
引理 6. 对于任意的 $t$ 和初始分布 $X_0, Y_0$,存在一个 coupling $(X_t), (Y_t)$,使得 $\Pr[X_t \ne Y_t] = \left\lVert P_{X_0}^t - P_{Y_0}^t\right\rVert$。
证明. $\color{red}{\text{Sorry.}}$(幽默,等我考完试再来写)
命题 2 的证明. 只需要证明 $\Delta(a + b) \leq 2\Delta(a)\Delta(b)$。考虑 coupling,对于任意的 $x_0$,定义 $X_0 = x_0, Y_0 = \pi$。有对于任意的 coupling,$\left\lVert P_X^t - \pi\right\rVert = \left\lVert P_X^t - P_Y^t\right\rVert \leq \Pr[X_t\ne Y_t]$。
注意到 $\Pr[X_{a + b} \ne Y_{a + b}] = \Pr[X_a \ne Y_a]\Pr[X_{a + b}\ne Y_{a + b} | X_a\ne X_b]$,根据最优 coupling 的存在性,存在一种 coupling 使得 $\Pr[X_a \ne Y_a] = \Delta(a)$。
现在,设 $X’_0 = \Pr[X_a | X_a \ne X_b], Y’_0 = \Pr[Y_a | X_a \ne X_b]$。有
$$
\begin{aligned}
\Pr[X_{a + b}\ne Y_{a + b} | X_a\ne X_b] &= \Pr[X’_b \ne Y’_b] \\
&= \left\lVert P_{X’_0}^t - P_{Y’_0}^t\right\rVert & \color{blue}{\text{(optimal coupling)}} \\
&\leq \left\lVert P_{X’_0}^t - \pi\right\rVert - \left\lVert P_{Y’_0}^t\right\rVert \\
&= 2\Delta(b)
\end{aligned}
$$
综上命题 2 成立。$\blacksquare$
接下来是一些应用。
随机交换洗牌. 每次随机选两个位置交换,问混合时间。
可以用一种趣味 coupling 分析出 $O(n^2)$ 的混合时间。
在 coupling 中,对于两堆牌 $(X_t, Y_t)$,我们随机两个数 $c, i$,然后将数字 $c$ 换到位置 $i$。
注意到这样不会让 $X_t, Y_t$ 的 Hamming distance 上升,而且只要随出的下标 $i$ 上的牌不一样,两堆牌中的 $c$ 位置不一样,Hamming distance 就会减一。因此相遇时间的期望是 $O(n^2)$,混合时间也便是 $O(n^2)$。
Remark. 最好的结果是 $O(n\log n)$ 的。