Yang Song, Stefano Ermon, Generative Modeling by Estimating Gradients of the Data Distribution (2019)
本文收录于 泛 AI 论文选读。
TL;DR
介绍了一种基于 denoising score matching 和 Langevin dynamics 采样的生成式模型。将 score matching 和 Langevin dynamics 结合起来是很自然的(形式上)。可能包含下面的 intuition:
- 为什么将分布建模成原始分布加高斯噪声? 解决流形假设带来的 score function 不良定义问题。
- 为什么添加不同水平的噪声,逐步去噪? 本质上是一种退火 Langevin dynamics 采样。
前置知识
Score Matching
在 上一篇文章 中我们介绍了 Score Matching 方法,需要注意的是补充的 Denoising Score Matching:
$$
\frac 12\mathbb{E}_{\boldsymbol{x}\sim p_{data}}\mathbb{E}_{\boldsymbol{\tilde{x}}\sim q(\boldsymbol{\tilde{x}} | \boldsymbol{x})} [\lVert\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{\tilde{x}}) - \nabla_{\boldsymbol{\tilde x}}\log q(\boldsymbol{\tilde{x}} | \boldsymbol{x})\rVert^2]
$$
Langevin Dynamics
存在一种在只知道 score function 时从原分布中采样的算法,称为 Sampling with Langevin dynamics。只需做如下迭代:
$$
\tilde{\boldsymbol{x}}_t = \tilde{\boldsymbol{x}}_{t - 1} + \frac{\epsilon}{2}\nabla_{\boldsymbol{x}}\log p(\tilde{\boldsymbol{x}}_{t - 1}) + \sqrt{\epsilon} \boldsymbol{z}_t
$$
这个算法的收敛性我们暂时无力严格分析。但是形象的展示可以参见 A Simplified Overview of Langevin Dynamics。结论是当 $\varepsilon \rightarrow 0$ 和 $T\rightarrow \infty$ 时,有 $\tilde{\boldsymbol{x}}_T \sim p(\boldsymbol{x})$。
这篇论文提出的生成式模型大概框架就是:训练时用 score matching 拟合分布的 score function,推理时用 langevin dynamics 采样。
基于 score matching 的生成式模型的问题
流形假设. 根据流形假设,现实世界中的图片倾向于集中在一个低维流形附近,这使得 score function 在一个稠密的区域定义不良。作者做了如下实验来证明该问题实际上也存在。
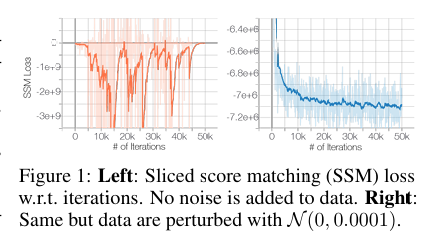
低密度区域. 原始分布中的低密度区域可能造成两方面影响:
Score Matching 不准确. 低密度区域可能没法产生足够的样本来帮助模型拟合出可信的 Score function。
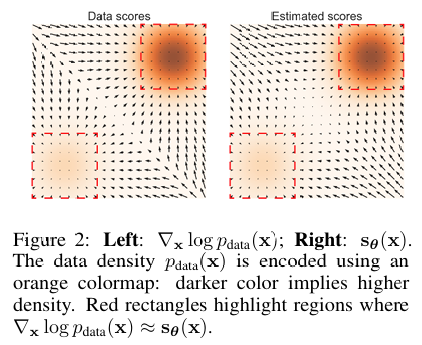
Langevin Dynamics 收敛慢. 低密度区域可能将整个分布分割成若干个岛,此时用 Langevin Dynamics 采样时,难以从一个岛转移到另一个岛。虽然理论上 Langevin Dynamics 产生正确的分布,但是 mixing time 非常大。
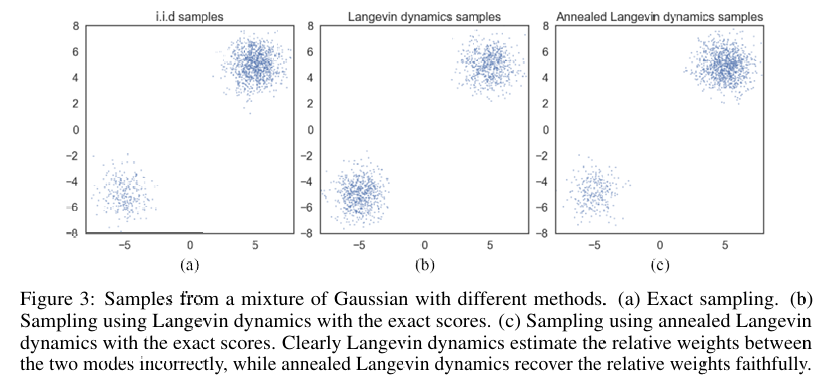
Noise Conditional Score Networks
作者提出了 NCSN 来解决上述问题。简而言之就是:
- 给训练数据添加不同等级的随机噪声。
- 用退火 Langevin 动力学来采样。
训练
形式化地,令 $\{\sigma_i\}_{i = 1}^L$ 是一列等比数列,其公比 $\dfrac{\sigma_i}{\sigma_{i - 1}} = q < 1$,这表示噪声等级。其中 $\sigma_1$ 应该大到能够克服上节所述的问题,而 $\sigma_T$ 应到小到人眼无法分辨。添加协方差为 $\sigma^2 \mathbf{I}$ 的高斯噪声之后,图像的概率分布为
$$
q_{\sigma}(\boldsymbol{\tilde{x}}) = \mathbb{E}_{\boldsymbol{x}\sim p_{data}}\left[\mathcal{N}(\boldsymbol{\tilde{x}} | \boldsymbol{x}, \sigma^2\mathbf{I})\right]
$$
在此处使用 denoising score matching,现在需要优化的目标是
$$
\mathscr{l}(\boldsymbol{\theta}; \sigma) := \frac 12\mathbb{E}_{\boldsymbol{x}\sim p_{data}}\mathbb{E}_{\boldsymbol{\tilde{x}}\sim q(\boldsymbol{\tilde{x}} | \boldsymbol{x})} [\lVert\boldsymbol{s}_{\boldsymbol{\theta}}(\boldsymbol{\tilde{x}}, \sigma) - \nabla_{\boldsymbol{\tilde x}}\log q(\boldsymbol{\tilde{x}} | \boldsymbol{x})\rVert^2]
$$
这里梯度无非是
$$
-\frac{\boldsymbol{\tilde{x}} - \boldsymbol{x}}{\sigma^2}
$$
注意 $\dfrac{\boldsymbol{\tilde{x}} - \boldsymbol{x}}{\sigma} \sim \mathcal{N}(0, \mathbf{I})$,所以理想情况下拟合出的 $\mathbf{s}_{\boldsymbol{\theta}}(\boldsymbol{\tilde{x}}, \sigma)$ 长度应当是 $1 / \sigma$ 级别的。因此我们需要定义一个总损失函数
$$
\mathcal{L}(\boldsymbol{x}, \{\sigma_i\}) = \sum_{i=1}^L \lambda(\sigma_i)\ell(\boldsymbol{\theta}, \sigma_i)
$$
时,为了平衡各网络的梯度,应当令 $\lambda(\sigma) = \sigma^2$。
推理
推理算法是一种退火 Langevin Dynamics 采样。
- 从 $\boldsymbol{x}_0$ 开始;
- For $i\leftarrow 1$ to $L$ do
- $\qquad$ $\alpha_i = \epsilon\cdot {\sigma_i^2} / \sigma_L^2$;
- $\qquad$ $\boldsymbol{x}_T \leftarrow \boldsymbol{x}_0$ 开始迭代 $T$ 步 $\epsilon = \alpha_i$ 的 Langevin 动力学采样;
- $\qquad$ 令 $\boldsymbol{x}_0\leftarrow \boldsymbol{x}_T$;