CS285 Part 1 - 模仿学习
尝试通过如下方法来解决序列决策过程:
- 通过让一个专家来做某一任务,获得大量的观察与标签。
- 用监督学习拟合人类的操作。
这个过程称作模仿学习(Imitation Learning)。
记号与术语
- 状态 $\mathbf{s}_t$
- 观察 $\mathbf{o}_t$
- 操作标签 $\mathbf{a}_t$
- 神经网络拟合到的分布 $\pi_{\theta}(\mathbf{a}_t | \mathbf{o}_t)$
其中 $t$ 表示时间步。操作可以是离散的选择,也可以是连续的。在离散的情况下,我们用 softmax 后的分布来刻画决策;在连续的情况下,我们可能用正态分布(通过给出 $\mu, \sigma$)之类的办法来刻画决策。
状态是指对整个物理场景的精确刻画,而观察是指传感器数据之类的表象。我们所谓的 Markov 决策过程是指某时间步的状态只取决于上一个时间步的状态和操作,但一般地观察并非具有马尔可夫性质,因此在实现模型时只考虑当前时间步的观察是不足够的,不妨考虑如下的例子:
一个老虎追赶一只羚羊,此时有一辆车遮挡了羚羊。
你可能需要知道前几个时间步的羚羊和车的位置,才能推断此时羚羊的位置。
一些简单介绍
本节说一些批话。
考虑一个生活中常见的场景:自动驾驶。很明显,这是一个 Markov Decision Problem。我们可能会考虑用摄像头来获得观察,然后用一个 CNN 来拟合决策与观察的关系。(以下图片都是从课件里截的)
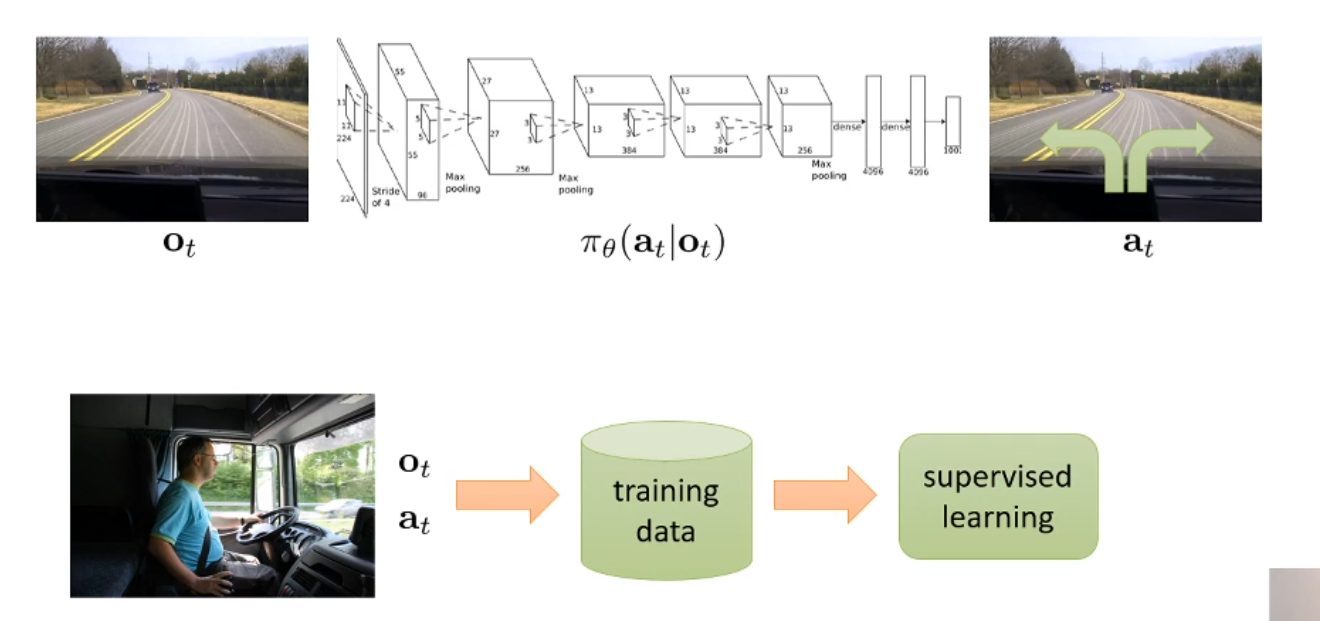
但容易想象这样的做法有如下的问题:
- 任何模型都会犯错误。
- 犯错误之后状态会偏离训练数据。
- 这样的误差随着时间累计,直到发生无法预计的状况。
这个问题称作分布漂移(distributional drift),换言之,神经网络拟合到了 $\pi_{\theta}$,训练数据采样到的状态的分布是 $p_{data}$,但是按照神经网络的决策,智能体实际上面临的状态分布变成了 $p_{\pi_{\theta}}$。当这两个分布相差很远的时候,误差就会陡增。可以形象地用下图展示:
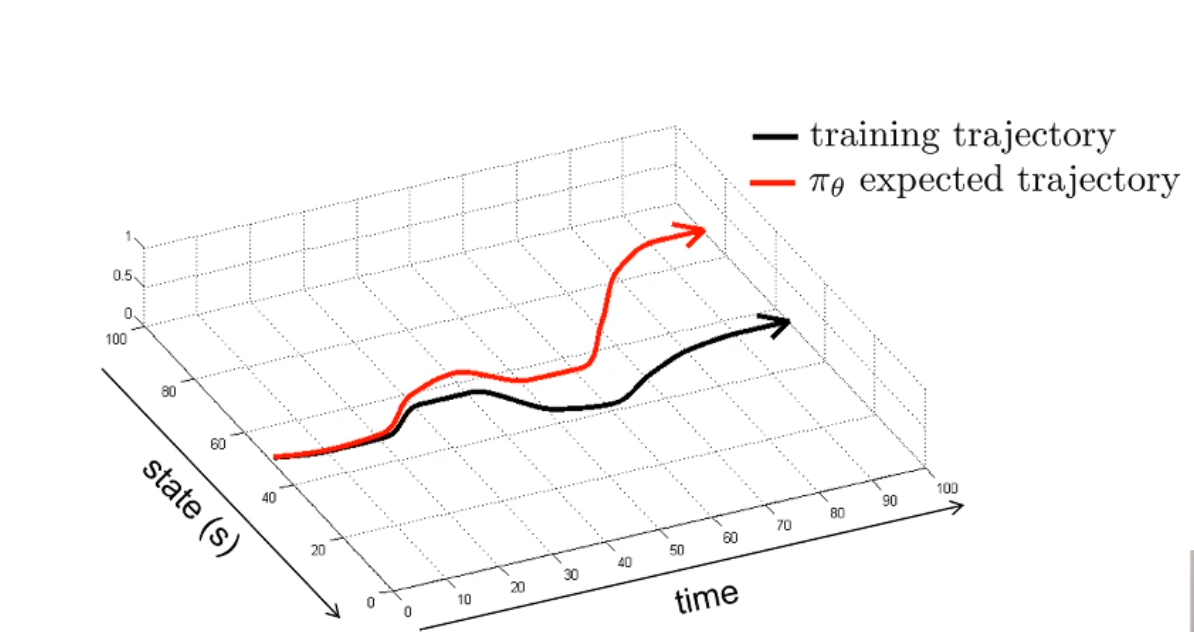
解决这个问题有两个符合直觉的办法:
- 让神经网络学会纠正小错误,做出近乎完美的决策。
- 让数据集变大,使得 $p_{\pi_{\theta}}$ 中可能出现的状况都在 $p_{data}$ 中。
让模型更好
可以通过增加额外的信息,来让模型学会实时纠正小错误。这来自 NVIDIA 的论文 End to End Learning for Self-Driving Cars。文章增加了两个侧方向的摄像头,然后做了数据增强。
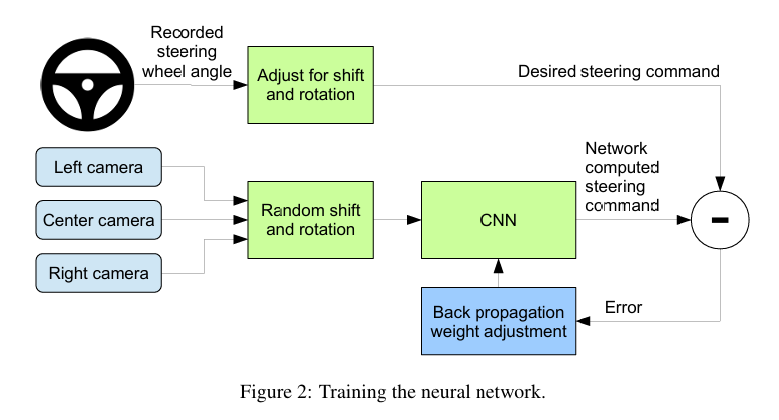
另外,模型没法学会专家的操作的原因,包括但不限于:
人类专家的操作可能是多模态的。不妨考虑如下的情况:
人类专家在避让相同障碍时,可能从左边也可能从右边。
在决策离散的情况下,模型可能不会有任何问题:Softmax 之后的分布很容易抓住这种分布在两端的情况。但是在连续的情况下如果我们用高斯分布来刻画决策的概率,$\mu$ 将会是可能的操作的均值,这时算法可能会决策“不做任何避让”。
人类专家的驾驶行为不是 Markov 的。
先解决第二个问题,我们熟知用 RNN / LSTM 之类的算法可以缓解这个问题。
对于第一个问题,一般有如下可能的办法:
- 将决策刻画成多个高斯分布的和。但这样所需高斯分布的个数可能是关于维数是指数级的。
- 使用 VAE 之类的隐变量模型。
- Autoregressive discretization。因为如果决策是离散的,那么没有什么问题,尝试把思路往这个方向靠近。这里只需要解决维数爆炸的问题,解决方法是:
- 首先用一个网络给出第一维的离散化决策。
- 从给出的分布里面采样。
- 将第一维的决策和观察同时喂给第二个神经网络,输出第二维的离散化决策。
- 迭代。
模型表现糟糕的原因还有一种,称作因果混淆(Causal Confusion)。考察如下情形:
有一辆车,在踩刹车时,刹车灯亮。人类专家在遇到突发情况(前面有人、红灯亮起时踩刹车)
算法只学会了刹车灯亮时踩刹车,因此没法处理突发情况。
使用 RNN 可能会加剧因果混淆。细节和解决的办法参见 Causal Confusion in Imitation Learning。
扩充数据集
下面是一种称为 DAgger(Data Aggregation) 的算法:
- 在数据集 $\mathcal{D} = \{(\mathbf{o}_1, \mathbf{a}_1), …, (\mathbf{o}_N, \mathbf{a}_N)\}$ 上监督学习,训练神经网络 $\pi_{\theta}(\mathbf{a}_t | \mathbf{o}_t)$。
- 运行该神经网络,得到一系列观察 $\mathcal{D}’ = \{\mathbf{o}_1, …\mathbf{o}_M\}$。
- 让人类来标注该观察。
- 令 $\mathcal{D} = \mathcal{D} \cup \mathcal{D}’$。
这个做法有一个小问题是在做第三步的时候,人类专家做的操作不会作用到场景中,这是很不自然的。从而可能会产生一些奇怪的问题。
分析
为了量化分布漂移的具体程度,我们可以定义奖励函数和损失函数,这两个函数本质上是一样的。下面我们展示两个例子,这是一个连续的奖励函数:
$$
r(\mathbf{s}, \mathbf{a}) = \log p(\mathbf{a} = \pi^*(\mathbf{s}) | \mathbf{s})
$$
这是一个离散的损失函数:
$$
c(\mathbf{s}, \mathbf{a}) = \begin{cases}
0 & \text{if $\mathbf{a} = \pi^{*}(\mathbf{s})$} \\
1 & \text{otherwise}
\end{cases}
$$
因为我们这里要做的是分析模型,所以不需要考虑函数光滑性之类的问题。唯一的要点是采用尽可能简单的离散的损失函数。我们可以用如下的期望来刻画分布漂移的程度:
$$
\mathbb{E}\left[\sum_t c(\mathbf{s}_t, \mathbf{a}_t)\right]
$$
下一小节是一个粗糙的分析:假设现在你的模型在训练集上误差的上界为 $\epsilon$,那么假设你一旦犯错就会接着继续犯错,那么 $T$ 时间内的总错误期望可以递归地表示为:
$$
E(T) \leq \epsilon T + (1 - \epsilon)E(T - 1)
$$
不难算出
$$
E(T) \leq \epsilon T^2 \label{ErrorBound}
$$
实际上在训练模型的过程中,你可能只能拿到某种平均误差,而不是一个总误差的 bound,假如给定
$$
\frac 1T\sum_{t}\mathbb{E}_{p_{\pi^*}(\mathbf{s}_t)}\pi_{\theta}(\mathbf{a}_t\ne \pi^*(\mathbf{s}_t) | \mathbf{s}_t) \leq \epsilon
$$
(记号有点垃圾,这里 $p_{\pi^*}(\mathbf{s}_t)$ 系指按照人类专家的操作得到的 $t$ 时间步的状态的分布)
我们首先可以给出 $p_{\theta}$ 和 $p_{\pi^*}$ 之间的 Total Varience 的上界:我们的目标是放缩
$$
\sum_{s_t} |p_\theta(\mathbf{s}_t) - p_{\pi^*}(\mathbf{s}_t)|
$$
假设你在前 $t$ 个时间步中,没有犯任何错误,则时间 $t$ 时的状态分布将就是 $p_{\pi^*}$。而如果你犯了一些错误,状态将服从另一些分布。总之我们将有
$$
p_{\theta}(\mathbf{s}_t) = \mathrm{Pr}[\text{No mistakes}] \cdot p_{\pi^*}(\mathbf{s}_t) + (1 - \mathrm{Pr}[\text{No mistakes}]) \cdot p’(\mathbf{s}_t)
$$
其中 $p’$ 是另一个分布,即犯错误之后的分布。于是
$$
\begin{align}
\sum_{\mathbf{s}_t}|p_\theta(\mathbf{s}_t) - p_{\pi^*}(\mathbf{s}_t)| &=\mathrm{Pr}[\text{making mistakes}] \cdot \sum_{\mathbf{s}_t} |p_{\pi^*}(\mathbf{s}_t) - p’(\mathbf{s}_t)|\\
&\leq 2\cdot\mathrm{Pr}[\text{making mistakes}]
\end{align}
$$
注意任意两个分布的 Total Variance 至多是 $2$。现在来放缩一下 $\mathrm{Pr}[\text{making mistakes}]$。
$$
\begin{align}
\mathrm{Pr}[\text{making mistakes}] &= \mathbb{E}_{\mathbf{s}_1, …, \mathbf{s}_{t}}\left[\mathrm{Pr}\left[\bigcup_{i=1}^{t} \mathbf{a}_i \ne \pi^*(\mathbf{s}_i))\right]\right] \\
&\leq \sum_{i=1}^{t} \mathbb{E}_{\mathbf{s}_1, …, \mathbf{s}_{t}}\left[\mathrm{Pr}[\mathbf{a}_i\ne \mathbf{s}_i]\right] \\
&= \sum_{i=1}^{t} \mathbb{E}_{\mathbf{s}_i}\pi_{\theta}(\mathbf{a}_i\ne \mathbf{s}_i | \mathbf{s}_i) \\
&\leq t\varepsilon
\end{align}
$$
因此
$$
\sum_{s_t} |p_\theta(\mathbf{s}_t) - p_{\pi^*}(\mathbf{s}_t)| \leq 2t\varepsilon
$$
这个界只在你将神经网络训练的足够好($\varepsilon < 1 / T$)时才比任意分布之间 Total Variance 的平凡上界要好。
接下来经过简单计算可以放出跟 $\ref{ErrorBound}$ 同样级别的界:
$$
\begin{align}
\mathbb{E}\left[\sum_t c(\mathbf{s}_t, \mathbf{a}_t)\right] &= \sum_{\mathbf{s}_t}\sum_t p_{\theta}(\mathbf{s}_t) c(\mathbf{s}_t, \mathbf{a}_t) \\
&\leq \sum_t \sum_{\mathbf{s}_t} p_{\pi^*} (\mathbf{s}_t) c(\mathbf{s}_t, \mathbf{a}_t) + |p_{\theta} - p_{\pi^*}| \cdot c_{\max} \\
&\leq \varepsilon T + \varepsilon T^2 = O(\varepsilon T^2)
\end{align}
$$
这个界的意义就是告诉你一个模仿学习的算法的安全性指标,比如可能辅助驾驶在一定时间之后就需要人类操控一下。另一方面,此界可以用于进一步分析 DAgger 的迭代次数。参见 A Reduction of Imitation Learning and Structured Prediction to No-Regret Online Learning
Homework 1: Imitation Learning Solution
我们尝试完成 23 Fall 的作业。
Analysis
第一小问结果已经整合在了上一节,第二小问很 trivial 不用做。
Experiment
代码题做实验做的云里雾里的,写了半天不知道我的 Performance 在哪里看,所以先咕了。我们还是做数学题吧。
Extra Credit: SwitchDAgger
本节考虑一个 DAgger 变种:SwitchDAgger。这是为了解决上文中提到的 DAgger 的一个缺点:人类专家需要在自己操作没有反馈的情况下提供策略指导,这是不自然的。
考虑一个 $T$ 时间步的 MDP,并假设专家策略为 $\pi^*$。在迭代 $n = 1, …, N$ 时,我们将会训练出一个不依赖于人类专家的策略 $\pi^n$。此时我们将模拟执行策略 $\pi^n$,然后在一个随机的时间步 $X^* + 1$ 将控制转交给专家直到模拟结束。
定义策略 $S^X(\pi_1, \pi_2)$ 表示在前 $X$ 个时间步执行 $\pi_1$ 策略,后面所有时间步都执行 $\pi_2$ 策略的一个策略。$\tilde \pi^n$ 表示 $S^X(\pi^n, \pi^*)$,其中 $X$ 是一个随机数。$\hat \pi^n$ 表示在第 $n - 1$ 次迭代产生的轨迹上拟合出的策略,拟合效果被如下的不等式刻画:
$$
\mathbb{E}_{s\sim p_{\tilde \pi_{n - 1}}}\mathrm{Pr}[\hat{\pi}^n(s)\ne \pi^*(s)]\leq \varepsilon
$$
SwitchDAgger 被定义为如下的迭代:初始时 $\tilde{\pi}^0 := \pi^*, \pi^0 := \hat{\pi}^1$,然后
- 在 $s\sim p_{\tilde{\pi}^{n - 1}}$ 上拟合 $\hat{\pi}^n$;
- 在几何分布 $\mathrm{Geom}(1 - \alpha)$ 上采样切换步数 $X_n + 1$,然后令 $\tilde{\pi}^{n}\leftarrow S^{X_n}(\hat{\pi}^n, \tilde{\pi}^{n - 1})$;
- 令 $\pi^n \leftarrow S^{X_n}(\hat{\pi}^n, \pi^{n - 1})$。
定义犯错误的次数为
$$
C(\pi) = \sum_{t = 1}^T \mathbb{E}_{s_t\sim p_{\pi}} \mathrm{Pr}[\pi(s_t)\ne \pi^*(s_t)]
$$
我们将要逐步证明 $C(\pi^n)$ 可以有一个 $O(T\varepsilon \log 1 / \varepsilon)$ 的 bound。
首先我们用一个递推式来刻画 $C(\tilde{\pi}^n)$ 的界。即存在 $A(t, n)$ 满足 $C(\tilde{\pi}^n)\leq A(T, n)$。
初值. 对于任意的 $t$,$A(t, 0) = 0$。因为 $\tilde{\pi}^0$ 是专家策略。对于任意的 $n$,$A(0, n) = 0$。
递推关系. 考察第一步是否移交策略。因为移交控制的步数服从几何分布 $\mathrm{Geom}(1 - \alpha)$,所以移交控制的概率为 $1 - \alpha$。
不移交控制,考虑是否犯错。若犯错,假设后面都会全错。那么期望犯错次数不会超过
$$
\begin{align}
&{\color{blue}{\alpha}}\mathbb{E}_{s\sim p_{\hat{\pi}^n}}\left[\mathrm{Pr}[\hat{\pi}^n(s)\ne \pi^*(s)]\cdot t + (1 - \mathrm{Pr}[\hat{\pi}^n(s)\ne \pi^*(s)])\cdot A(t - 1, n)\right]
\end{align}
$$需要注意的是无论如何 $A(t - 1, n)$ 都不会超过 $t$,所以此处可以将概率悉数放到最大,套用 $\hat{\pi}^n$ 的拟合效果立即得到这部分犯错次数不超过
$$
\alpha \varepsilon t + \alpha (1 - \varepsilon) A(t - 1, n)
$$移交控制,递归得到期望犯错次数被 $A(t, n - 1)$ bound 住。
综上得到递推关系:
$$
A(t, n) = \alpha\varepsilon t + \alpha (1 - \varepsilon)A(t - 1, n) + (1 - \alpha) A(t, n - 1)
$$
警告. 接下来我们将 input 一个神秘结论,来自作业题的第二问。
可以证明
$$
C(\tilde{\pi}^n) \leq Tn\alpha\varepsilon \label{wtf_bound}
$$
但是取 $n = 1, \alpha = 1$,这个就退化成了不做 DAgger,这样居然能分析出来一个 $T\varepsilon$ 的界,比之前分析的 $O(T\varepsilon^2)$ 好了一个级别??总之这个界肯定不是 General 的,在 $\alpha \leq 1 / T$ 的时候可能是对的,可以归纳一下。这里摆了。
然后需要注意到 $C(\pi^n)$ 和 $C(\tilde{\pi}^n)$ 之间差的并不远,因为他们之间只有最后一小段是不一样的。根据 Chernoff bound 当 $n \geq T, \alpha \leq 1 / T$ 时,有
$$
\mathrm{Pr}\left[\sum_{i=1}^n X_n\leq T\right] = \exp\left(\frac{-n}{(1-\alpha)T}\right)
$$
如果没有覆盖最后一小段,假设它会全错,那么显然
$$
C(\pi^n) \leq C(\tilde{\pi}^n) + T\exp\left(\frac{-n}{(1-\alpha)T}\right)
$$
只需取 $n = T\log 1/\varepsilon, \alpha = 1 / T$,即可获得一个 $O(T\varepsilon\log1/\varepsilon)$ 的界。但他第二小问这个 $\ref{wtf_bound}$ 实在是太怪了,也不知道怎么证的。