Qisheng Wang, Mingsheng Ying. Quantum Algorithm for Lexicographically Minimal String Rotation (2022)
Abstract. 本文是 https://doi.org/10.1007/s00224-023-10146-8 的阅读笔记。他们提出了求字符串最小字典序后缀的 $O(n^{3/4})$ 量子算法,但感觉非常套路。文章还证明了这个问题的平均复杂度下界 $\Omega(n^{1/2} / \log^{1/2} n)$ 和最坏复杂度下界 $\Omega(n^{1/2})$,但他自己并没有达到这个界。
定义
字符串的最小字典序循环移位是一个经典问题。
本文提出一个最差复杂度 $O(n^{3/4})$ 的算法来解决这个问题,平均复杂度可以被优化到 $O(\sqrt n\log n)$。
我们假设给定了如下的 Oracle 用于访问字符串 $s$:
$$
U_{\mathrm{in}}|i, j\rangle = |i, j \oplus s_i\rangle
$$
以下是一些记号:
- $s^{(k)}$ 表示 $s$ 做 $k$ 次循环移位。
- $\mathrm{LCP}(s, t)$ 表示 $s, t$ 的最长公共前缀。
- $\mathrm{SCR}(s)$ 表示 $s$ 字典序最小的循环移位 $\min\{s^{(0)}, …, s^{(n - 1)}\}$。
- $\mathrm{LMSR}(s)$ 表示对应的下标 $\arg \min_k \{s^{(k)}\}$。
一些朴素 / 前置的结果
定理 2.1.1. 存在一个常数概率正确的算法,在 $O(\sqrt n)$ 内比较两个长度为 $n$ 的字符串 $s, t$ 的字典序。
因为可以构造一个 Oracle 来返回字符串的两位是否相同,然后通过 [DH96] 中的算法来找到最小值即 $\mathrm{LCP}(s, t)$ 的下一位。接下来的步骤是平凡的。
定理 2.1.2. 存在一个常数概率正确的算法,在 $O(\sqrt{n\log^3 n\log\log n}) = \tilde{O}(\sqrt n)$ 内求一个字符串的 deterministic sampling。
定理 2.1.3. 存在一个常数概率正确的算法,在 $\tilde{O}(\sqrt n + \sqrt m)$ 的复杂度内求一个长为 $m$ 的字符串 $t$ 在长为 $n$ 的字符串 $s$ 中出现的最小位置。
Deterministic Sampling 的定义参见 [Vi91],上述两算法参见 [RV03]。
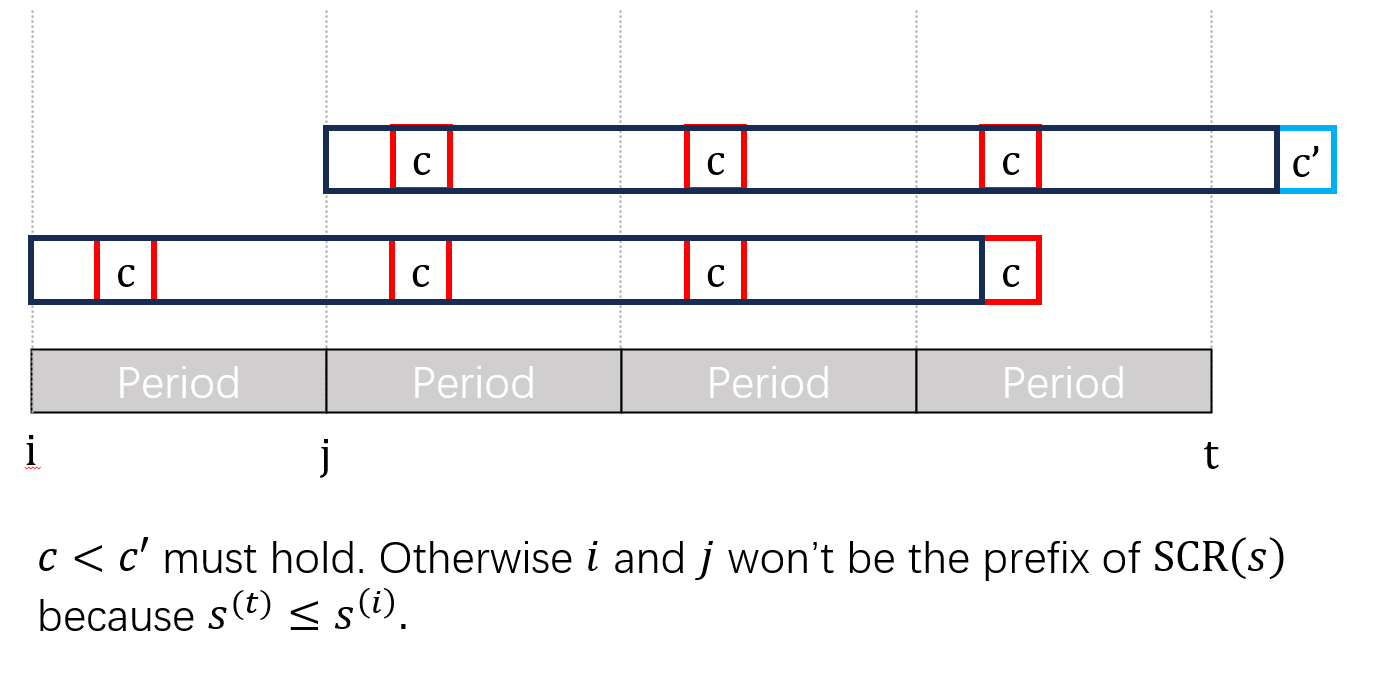
定理 2.1.3. 若两个长度为 $L$ 的子串 $s[i, .., i+L-1], s[j, …, j+L-1]$ 都是 $\mathrm{SCR}(s)$ 的前缀,且 $i < j \wedge j-i < L / 2$,那么 $j$ 绝无可能是 $\mathrm{LMSR}(s)$。
证明.
不言而喻,一目了然。
基础算法
我们的算法几乎是照搬字符串算法设计的套路。算法的大概组织如下,有一个超参数 $B$:
- 先找到 $\mathrm{SCR(s)}$ 的长度为 $B$ 前缀。
- 将下标分成长度为 $B$ 的块后:
- 在块内使用某种互斥原则排除一些候选,最后只保留 $O(1)$ 个候选。
- 在块间求出最终的答案
第一部分 找 $\mathrm{SCR}$ 的长度为 $B$ 的前缀
根据定理 2.1.1. 存在一个 $\sqrt B$ 的 Oracle $U_{\mathrm{cmp}_B}$ 来比较长度为 $B$ 的字符串的字典序。用此函数求出整个字符串中字典序最小的串 $p = S[i^*, …, i^* + B - 1]$,其中 $i^* \in [n]$,复杂度为 $O(\sqrt{nB})$
分块
我们将序列分成长度为 $L = \lfloor B / 4\rfloor$ 的块。
第二部分 第一层 在块内使用某种互斥原则排除一些候选
因为现在有了 $i^*$,根据定理 2.1.2,我们可以在 $\tilde{O}(\sqrt n)$ 复杂度内求出 $p$ 的 deterministic sampling。
显然我们可以在 $\tilde{O}(\sqrt B)$ 复杂度内找到第一个匹配上 $p$ 的位置,这个位置称为第 $j$ 块的候选 $h_j$。
第二部分 第二层 在块间选出最终答案
显然这时候我们求所有块间候选的中字典序最小的即可。我们只需要设计比较函数 $\mathrm{cmp}(i, j)$,此函数先求 $h_i, h_j$,然后比较其字典序大小,用时 $O(\sqrt{B\log B} + \sqrt n)$,大头是 $O(\sqrt n)$。
然后用 $\mathrm{cmp}$ 函数运行 [DH96] 中的算法,即得到答案。
这一层复杂度为 $O(\sqrt{n / B}(\sqrt{B\log B} + \sqrt N)) = O(n / \sqrt B)$
算法分析
显然最后复杂度是 $O(\sqrt{nB} + n / \sqrt{B})$,置 $B = \sqrt n$ 得到最低复杂度 $O(n^{3/4})$。
将平均复杂度优化至 $\tilde{O}(\sqrt n)$
在字符串问题谈平均复杂度纯耍流氓,在 OI 里面都是只能拿 $10$ 分的水平,因为你知道这样两个串的 $\mathrm{LCP}$ 期望是 $\log$ 的。因此你也不难想象他想要干什么。我们这里就不讲了。
复杂度下界证明
复杂度下界的证明采用了 Ambainis 和 de Wolf 的工作,他们将一个布尔函数的计算复杂度下界和其块敏感度联系了起来。
对于 $S\subset [n]$,我们记 $x^S$($x$ 关于 $S$ 翻转)为
$$
\left(x^S\right)_i = \begin{cases}
\bar{x}_i & i\in S \\
x_i & i\notin S
\end{cases}
$$
定义 6.1(Block Sensitivity). 函数 $f$ 在输入 $x$ 上的块敏感度定义为最大的 $m$ 使得存在不相交的集合 $S_1, …, S_m$,使得
$$
f(x) \ne f(x^{S_i}) \quad \forall 1\leq i\leq m
$$
定理 6.2([AdW99], Theorem 6.3). 对于任意的布尔函数 $f: \{0, 1\}^n\rightarrow \{0, 1\}$ 和概率分布 $\mu : \{0, 1\}^n\rightarrow [0, 1]$,量子算法的平均复杂度下界
$$
Q^\mu(f) = \Omega\left(\mathbb{E}_{x\sim \mu}\left[\sqrt{bs_x(f)}\right]\right)
$$
现在我们定义 $\mathrm{LMSR}_0(x) = \mathrm{LMSR}(x)\bmod 2$。显然
$$
\mathbb{E}_{x\sim \mu}\left[\sqrt{bs_x(\mathrm{LMSR}_0)}\right] \leq Q^\mu(\mathrm{LMSR}_0) \leq Q^\mu(\mathrm{LMSR})
$$
现在任务是给出 $bs_x(\mathrm{LMSR}_0)$ 的下界。首先可以不失一般性地假设 $\mathrm{LMSR}(x) = 0$,因为如果 $\mathrm{LMSR}(x) = k$,那么可以先对着 $x^{(k)}$ 构造 $S_1^{(k)}, …, S_m^{(k)}$,然后令 $S_i = S_i^{(k)} + k$ 即可。
我们构造的整体思路是:选择一个奇数下标,将后面一段序列全部改成 $0$,来强行让它比 $x^{(0)}$ 小。回忆在串纯随机的情况下,两个位置的 $\mathrm{LCP}$ 不会很大。我们形式化这一件事情。
Warning. 下面的定义是我自己想的,因为我觉得他的定义实在是很不直观。但应该也是对的。
定义 6.3. 对于字符串 $s$,定义
$$
C(s) = \max\{\mathrm{LCP}(s, s^{(i)}) : 0 < i < n\}
$$
引理 6.4. 若均匀随机采样 $s$,那么 $C(s)$ 超过 $B < n / 2$ 的概率不会很大。
$$
\mathrm{Pr}\left[C(s) \leq B\right] \geq 1 - O\left(n|\Sigma|^{-B}\right)
$$
证明. 将补事件用 Union Bound 拆开。
$$
\begin{align}
\mathrm{Pr}\left[C(s) \leq B\right] =& 1 - \mathrm{Pr}\left[C(s) > B\right] \\
\geq& 1 - \sum_{i = 1}^{n - 1}\mathrm{Pr}\left[\mathrm{LCP}(s, s^{(i)}) > B\right] \\
\geq& 1 - \sum_{i = 1}^{n - 1}|\Sigma|^{-B} \\
=& 1 - O\left(n|\Sigma|^{-B}\right)
\end{align}
$$
Remark. 因为这里是 $01$ 串,所以 $|\Sigma| = 2$。
取 $B = O(2\log n)$ 得到
推论 6.5.
$$
\mathrm{Pr}[C(s) \leq 2\log n] = 1 - O\left(\frac 1n\right)
$$
接下来的引理表明给出我们对 $S_1, …, S_m$ 的构造。
引理 6.6. 对于 $x$,若 $C(x) \leq n / 5$,那么
$$
bs_x(\mathrm{LMSR}_0) \geq O\left(\frac{n}{4C(x)}\right)
$$
证明. 设 $B = C(x)$,我们将序列分成长度为 $4B$ 的块,$\mathcal{B}_i$ 定义为第 $i$ 块的下标集合(从 $\mathcal{B}_0$ 开始)。那么根据 $C(x)$ 的定义,即便是 $s$ 的开头也不存在连续 $2B - 2$ 个 $0$。因此我们将连续 $2B - 1$ 个位置都调整为 $0$,即可让该位置开始的循环移位成为 $\mathrm{LMSR}$。那么恰当取异或,可以让 $s_{\mathcal{B}_i}$ 变成 $100…0$ 或者 $1100…0$,从而这一段后缀 $0$ 将成为 $\mathrm{LMSR}$,只需要根据 $\min \mathcal{B}_i$ 的奇偶性选择即可。
综合起来我们得到了最终结论
定理 6.7(LMSR 的平均复杂度下界). 若 $\mu$ 是 $2^n$ 上的均匀分布,则
$$
Q^\mu(\mathrm{LMSR}) = \Omega\left(\sqrt{\frac{n}{\log n}}\right)
$$
证明. 根据上述结果
$$
\begin{align}
Q^\mu(\mathrm{LMSR}) \geq& \mathbb{E}_{x\sim \mu}\left[\sqrt{bs_x(\mathrm{LMSR}_0)}\right] \\
=& \frac{1}{2^n}\sum_{x\in\{0, 1\}^n} \sqrt{\frac{n}{4C(x)}} \\
\geq& \frac{1}{2^n}\sum_{x\in\{0, 1\}^n, C(x) \leq 2\log n} O\left(\sqrt{\frac{n}{\log n}}\right) \\
=& O\left(\sqrt{\frac{n}{\log n}}\right)\mathrm{Pr}_{x\sim \mu}\left[C(x) \leq 2\log n\right] \\
=& O\left(\sqrt{\frac{n}{\log n}}\right)
\end{align}
$$
最坏复杂度的下界非常好证明。[AdW99] 同时给出了量子算法的时间下界在最坏情况下的版本:
定理 6.8([AdW99]). 对于布尔函数 $f : \{0, 1\}^n\rightarrow \{0, 1\}$,任意高概率正确的量子算法 $A$ 在输入 $x$ 上的运行时间
$$
T_A(x) = \Omega\left(\sqrt{bs_x(f)}\right)
$$
而 $bs_{1^n}(\mathrm{LSMR}_0) \geq n / 2$,因为你任意翻转一个奇数位置就可以改变 $\mathrm{LSMR}_0$。
所以这篇文章给出的上下界之间还有一定差距。
参考文献
[DH96] C. Dürr, P. Hoyer. A quantum algorithm for finding the minimum. Quantum Physics E-Print Archive. http://xxx.lanl.gov/quant-ph/9607014. 1996
[Vi91] Uzi Vishkin. Deterministic Sampling–A New Technique for Fast Pattern Matching. SIAM Journal on Computing 1991 20:1, 22-40
[RV03] H. Ramech, V.Vinay. String matching in $\tilde{O}(\sqrt n + \sqrt m)$ quantum time (2003)
[AdW99] A. Ambainis, R. de Wolf, Average-case quantum query complexity. Journal of Physics A General Physics, 34(35): 6741-6754, 1999