Revision | 音乐与数学
基础知识
定义 1.1(e.g.《中国大百科全书·音乐舞蹈》). 音乐系指凭借声波振动而存在、在时间中展现、通过人类的听觉器官而引起各种情绪反应和情感体验的艺术门类。
众所周知声波是纵波,声音的几个物理属性对应音乐中的几个要素:
频率对应音高。
人耳能听见的范围是 $20$ 至 $20000$ Hz。
定义 1.2(音乐会音高). 中央 $\textsf{C}$ 上方的 $\textsf{A}$ 为 $440 \textrm{ Hz}$。
人类对于频率的感知不是线性的(增加一个八度,频率乘 2)。
振幅对应力度。气压决定响度(注意这里力度和响度有主观和客观的区别)。
当频率为 $1000 \textrm{ Hz}$ 时,人类的听觉下限阈值为 $p_0 = 20\mu Pa$。
定义 1.3(声压水平,SPL).
$$
L_p = 20\log_10\left(\frac{p}{p_0}\right)
$$单位是分贝(dB)。
持续时间对应时值。
波形对应音色。
谈论音色的时候我们通常从时间包络、频谱两个面入手。
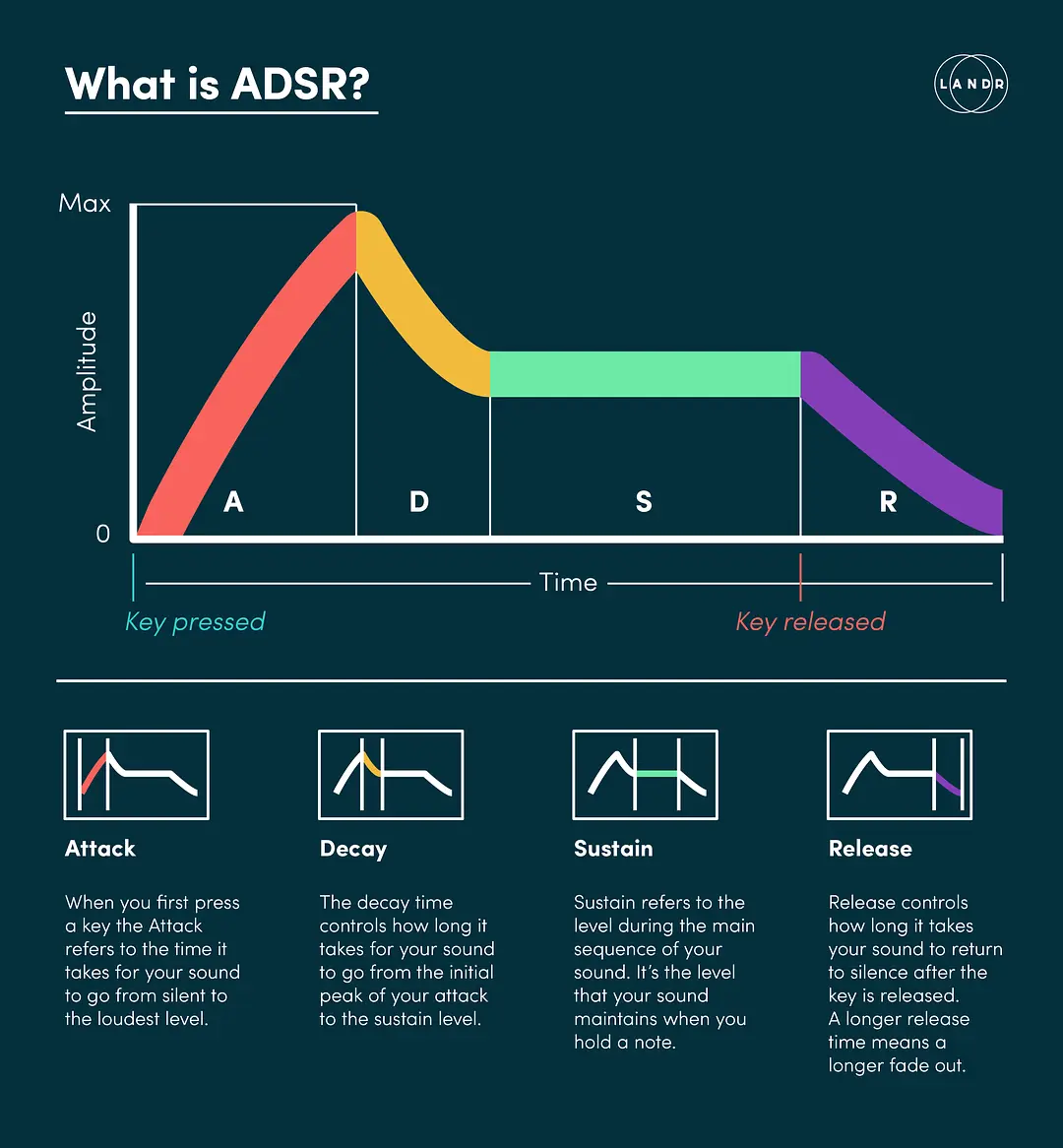
通过做振幅的包络线可以直观展示乐器的音色,可以发现弹奏乐器时振幅的变化一般可以用四个阶段(Attack 起音;Decay 衰减;Sustain 持续;Release 释放)来刻画。这称作 ADSR,在一些电子音乐制作软件
通常的声音都是不同频率的振动的叠加。通过对振幅的时域信号做傅里叶展开,可以得到各个成分的振幅。
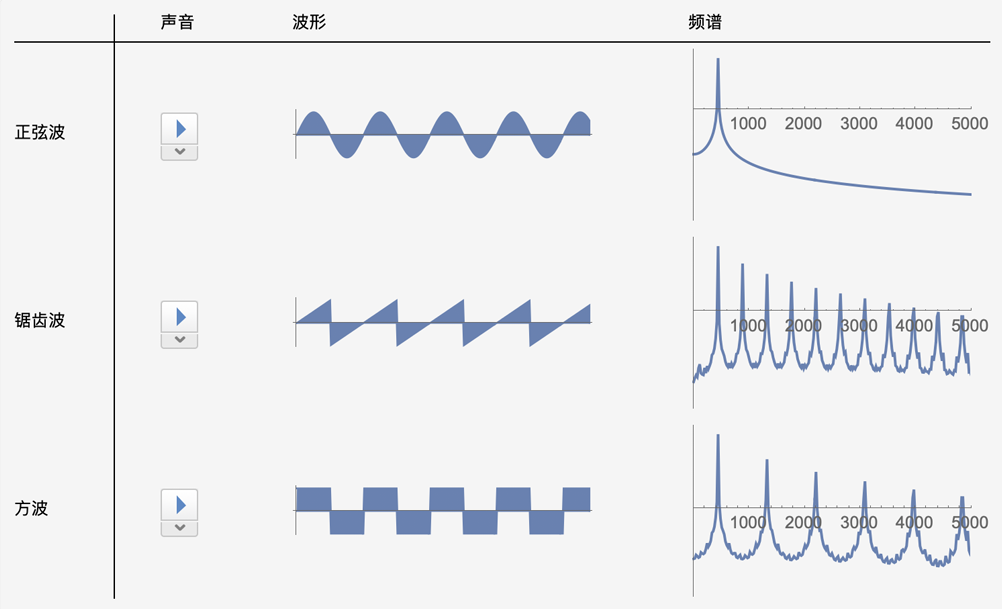
将各频率成分从低到高排列,称作泛音列。
乐音体系
声音分为乐音和噪音两类,划分标准为振动是否有规律性。
音乐中噪音的使用
传统音乐作品主要使用乐音,二十世纪以来音乐家越来越重视对于噪音的使用。
打击乐器可以分为固定音高和无固定音高的,后者发出的就属于噪音。
一些例子:谭盾的《地图协奏曲》(使用一些神秘原始打击乐比如撞击石头)、柴可夫斯基的 1812 Overture, Op.49(使用加农炮)
音乐中所使用的具有固定音高的全体乐音构成的集合称作乐音体系,其中元素称作音级。将全体音级从低到高排列得到的序列称作音列,其中相邻两元素之差称作一个半音。
钢琴中最接近的两个键(包括黑键和白键)相差一个半音。
每个音级有一个名字,称作音名。基本的音名只有 $\textsf{C}, \textsf{D}, \textsf{E}, \textsf{F}, \textsf{G}, \textsf{A}, \textsf{B}$,在每个八度中循环使用。为了区分八度,加上角标。常见的钢琴键从 $\textsf{A}_0$ 到 $\textsf{C}_8$,中央 $\textsf{C}$ 指 $\textsf{C}_4$。
$\textsf{C}, \textsf{D}, \textsf{E}, \textsf{F}, \textsf{G}, \textsf{A}, \textsf{B}$ 也称作基本音级。在基本音级前方加上变音记号($\sharp, \flat, \natural, \flat\flat$,和一个 LaTeX 打不出来的 $^\mathbf{x}$ 状的重升号),得到变化音级。
注意 $\textsf{E}$ 和 $\flat\textsf{F}$ 实际上是同一个音,这种现象称作等音。
我们生活中常用的 do,re,mi,fa,sol,la,si 称为唱名,唱名的确定有两种方式:
- 固定唱名法:do 指 $\textsf{C}$。
- 首调唱名法:do 指任意一音级,其后 re,mi,fa,so,la,si 依次在前一个的基础上增加全、全、半、全、全、全音。
记谱法
以书面形式记录音乐的方法称为记谱法。
一些材料
《礼记·投壶》中的鼓谱:“圆者击鼙,方者击鼓”(郑玄注)

中国留传最早的乐谱:《碣石调·幽兰》,属于文字谱。

将古琴的指法和弦序、徽位结合成文字的谱称作减字谱。

还有一种传统汉字记谱法称作工尺谱。

现在主流的记谱方法是五线谱,这里不再赘述五线谱上的记号。
音程
乐音体系中,两个音级之间的距离称作音程,其中较高的称作冠音,较低的称作根音。音程中的两个音先后发声称作旋律音程,同时发声称作和声音程。
刻画一个音程需要描述根音和冠音之间的音名数量和半音数量。据此音名可以被命名为 $\square X$ 度,其中 $X$ 指示音名数量,$\square$ 用纯、大、小、增、减等字眼来提示半音数目。我们将以 $\textsf{C}$ 作为根音,$\textsf{C}, \textsf{F}, \textsf{G}, \textsf{C}’$ 为冠音得到的音程(以及有其他根音、冠音但是间隔相同唱名数和半音数的音程)称作纯音程;$\textsf{D}, \textsf{E}, \textsf{A}, \textsf{B}$ 为冠音得到的音程称作大音程。
音程 $\textsf{C}-\textsf{G}$ 按照上面的规则被命名为”纯五度“。
下面所说的将一个音程“扩大一个半音”系指将根音降低一个半音或将冠音升高一个半音,类似地定义“缩小一个半音”。
我们继续规定其他可能的音程的命名:
- 将大音程缩小一个音程,得到小音程。
- 将大音程或者纯音程扩大一个半音,得到增音程。
- 将小音程或者纯音程缩小一个半音,得到减音程。
下表给出了一些诸音程的具体例子,括号中的数字是半音数
| 减 | 小 | 纯 | 大 | 增 | |
|---|---|---|---|---|---|
| 一度 | $\textsf{C}-\textsf{C}(0)$ | $\textsf{C}-\sharp\textsf{C}(1)$ | |||
| 二度 | $\sharp\textsf{C}-\flat\textsf{D}(0)$ | $\textsf{C}-\flat\textsf{D}(1)$ | $\textsf{C}-\textsf{D}(2)$ | $\textsf{C}-\sharp\textsf{D}(3)$ | |
| 三度 | $\sharp\textsf{C}-\flat\textsf{E}(2)$ | $\textsf{C}-\flat\textsf{E}(3)$ | $\textsf{C}-\textsf{E}(4)$ | $\textsf{C}-\sharp\textsf{E}(5)$ | |
| 四度 | $\sharp\textsf{C}-\textsf{F}(4)$ | $\textsf{C}-\textsf{F}(5)$ | $\textsf{C}-\sharp\textsf{F}(6)$ | ||
| 五度 | $\sharp\textsf{C}-\textsf{G}(6)$ | $\textsf{C}-\textsf{G}(7)$ | $\textsf{C}-\sharp\textsf{G}(8)$ | ||
| 六度 | $\sharp\textsf{C}-\flat\textsf{A}(7)$ | $\textsf{C}-\flat\textsf{A}(8)$ | $\textsf{C}-\textsf{A}(9)$ | $\textsf{C}-\sharp\textsf{A}(10)$ | |
| 七度 | $\sharp\textsf{C}-\flat\textsf{B}(9)$ | $\textsf{C}-\flat\textsf{B}(10)$ | $\textsf{C}-\textsf{B}(11)$ | $\textsf{C}-\sharp\textsf{B}(12)$ | |
| 八度 | $\sharp\textsf{C}-\textsf{C}’(11)$ | $\textsf{C}-\textsf{C}’(12)$ | $\textsf{C}-\sharp\textsf{C}’(13)$ |
注意因为有等音的存在,不同的音程听起来一样是很正常的现象。
同时弹奏不同的音程给人以不同的听觉感受,一些听起来是和谐的,另外的则比较难听。纯四度、纯五度、纯八度、大小三度、大小六度属于协和音程,其中纯音程完全协和,三度和六度不完全协和;二度、七度和增减音程均属于不协和音程。
有若干理论用来解释音程是否和谐。
毕达哥拉斯理论
长度之比为简单整数比的弦能发出和谐的声音。根据后面的结果,这就是说振动频率之比越简单,相应音程越协和。
这个理论是当时律制下的结果,如果按照十二平均律调音,那么频率比全是无理数,按理说应该非常难听,但实际上并不是这样。
Helmholtz 拍音理论 注意到频率为 $\omega$ 和 $\omega + \delta$ 的声音叠加之后是
$$
\sin(2\pi(\omega + \delta)t) + \sin(2\pi\omega t) = 2\sin\left(2\pi(\omega + \frac{\delta}{2})t\right)\cos \pi\delta t
$$
这类似于将 $\cos\pi\delta t$ 调制在一个频率为 $\omega + \delta / 2$ 的波上
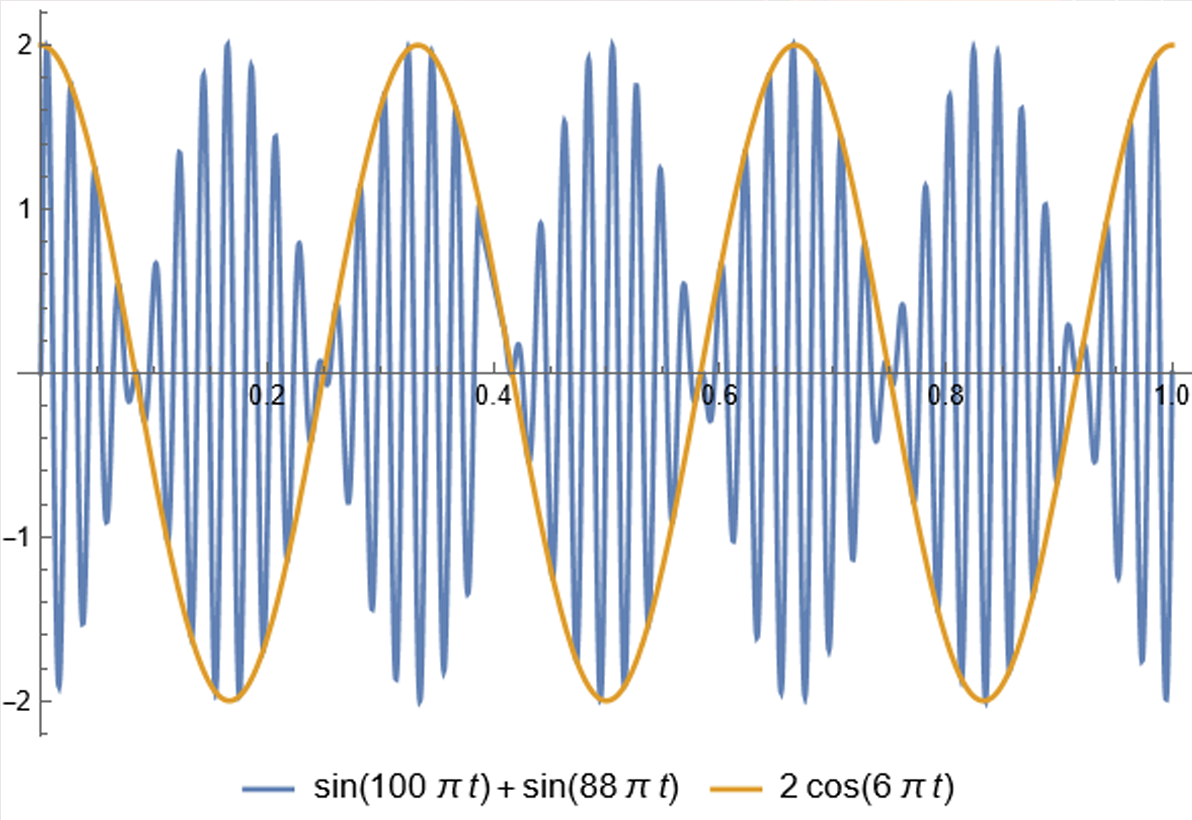
那么将这两个声音叠加之后,将会产生每秒 $\delta$ 次的“震荡”的声音(读者可以自行用音频软件模拟,确实很明显),称作拍音。
Helmholtz 认为每秒少于 $6$ 个或者多于 $120$ 个拍音的音程不协和,每秒 $33$ 个拍音的最不协和。
但是这个理论缺陷很明显,因为升高八度频率乘二,所以这就导致一个非常不协和的音程升高几个八度就协和了,这自然是不对的。
Stumpf 心理学实验结果
让未经过音乐训练的被试分别听到的声音(可能是单个音,也可能是同时演奏根音和冠音)是一个声音还是两个声音。
实验表明将音程混同做一个音的比例排序是八度(75%),五度(50%),四度(33%)。
1987 年 L.A.DeWitt, R.G.Crowder 拓展了他们的结果,增加了可能的要素比如反应时间、泛音、不同律制等。
文化背景?
调式
若干音级围绕一个有稳定感的中心音级,按照一定音程关系组织在一起的乐音体系称作调式。该中心音级称作主音。
将调式中的音级从主音开始按照高低次序排列起来,直到高八度的主音,得到(调式)音阶。例如 $\textsf{D}$ 大调音阶:
$$
\textsf{D} \quad \textsf{E} \quad \sharp\textsf{F} \quad \textsf{G} \quad \textsf{A} \quad \textsf{B} \quad \sharp\textsf{C} \quad \textsf{D}
$$
在大小调体系中将音阶中的音级从低到高依次编号和命名为:$\mathrm{I}$ 主音、$\mathrm{II}$ 上主音、$\mathrm{III}$ 中音、$\mathrm{IV}$ 下属音、$\mathrm{V}$ 属音、$\mathrm{VI}$ 下中音、$\mathrm{VII}$ 导音。
以下是几种常见的调式音阶:
- 自然大调 从主音开始,向上依次增加大二度、大二度、小二度、大二度、大二度、大二度、小二度。($\textsf{C}$ 大调:钢琴上从 $\textsf{C}$ 开始向后八个白键)
- 自然小调 从主音开始,向上依次增加大二度,小二度,大二度,大二度,小二度,大二度,大二度。($\textsf{A}$ 小调:钢琴上从 $\textsf{A}$ 开始向后八个白键)
- 和声小调 将自然小调的第 $\mathrm{VII}$ 级导音升高半音。注意这样第 $\mathrm{VI}$ 和 $\mathrm{VII}$ 级之间是一个增二度。
- 旋律小调 将自然小调 $\mathrm{VI}$ 和 $\mathrm{VII}$ 级都升高一个半音。
注意 和声小调和旋律小调额外的升号不写在调号上!
注意在记谱时,有些音级总是需要升高半音(比如 $\textsf{D}$ 大调中的 $\textsf{C}$、$\textsf{F}$),因此简便起见,我们将需要升高半音的音级在五线谱的谱号后方标注出,称作调号。美观起见,我们总是只在基本音级上统一地写 $\flat$ 或者 $\sharp$。
注意到 $\textsf{C}$ 大调、$\textsf{A}$ 小调无需任何升降,主音升高 / 降低一个纯五度,只有一个位置需要添加 $\sharp$ / $\flat$。因此
- $\textsf{C}, \textsf{G}, \textsf{D}, \textsf{A}, \textsf{E}, \textsf{B}, \sharp\textsf{F}, \sharp\textsf{C}$ 大调依次有 $0, 1, …, 7$ 个 $\sharp$。
- $\textsf{C}, \textsf{F}, \flat\textsf{B}, \flat\textsf{E}, \flat\textsf{A}, \flat\textsf{D}, \flat\textsf{G}, \flat\textsf{C}$ 大调依次有 $0, 1, …, 7$ 个 $\flat$。
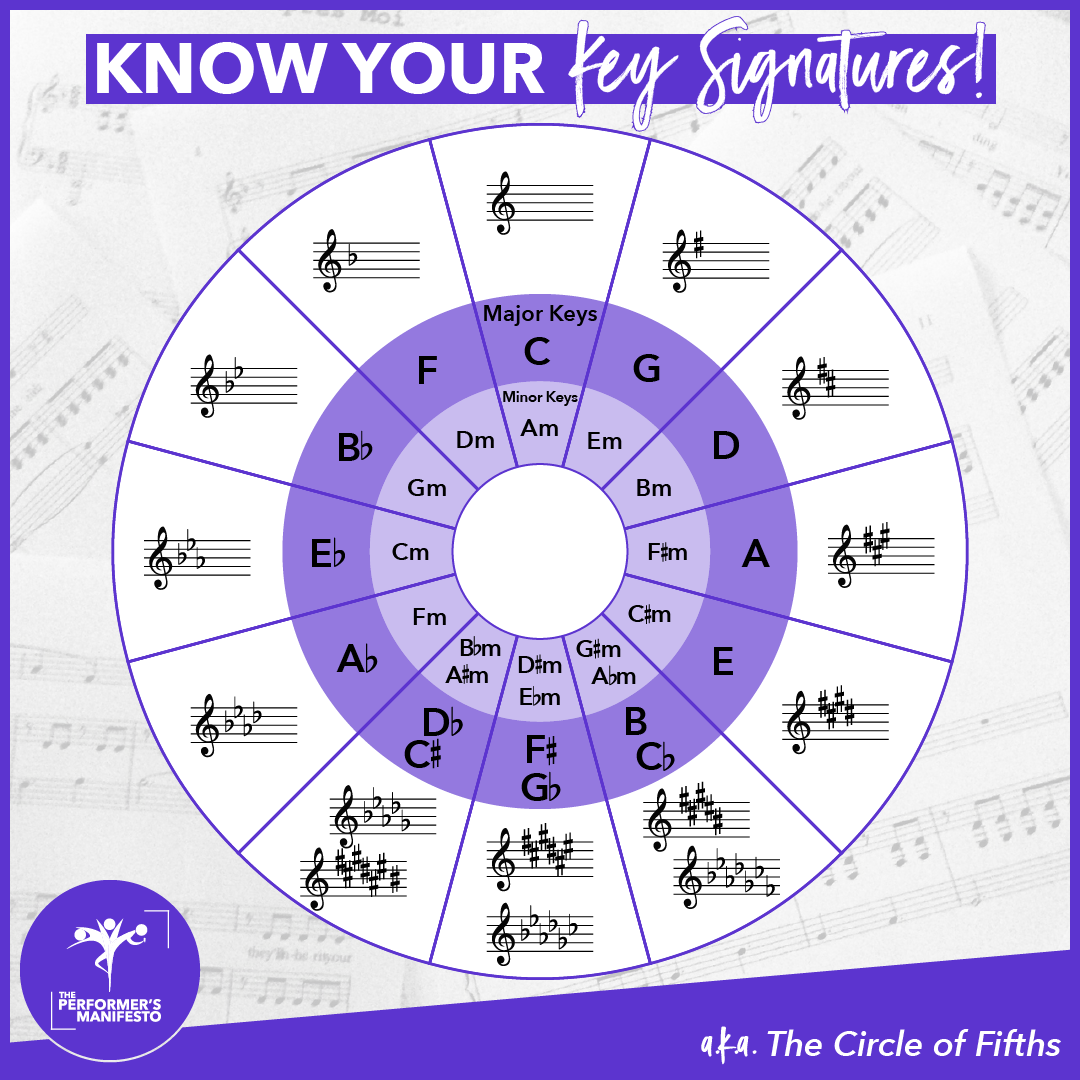
显然调式中各种等音之类的现象是广泛存在的。
- 等音调 音阶完全相等的两个调,如 $\sharp \textsf{C}, \flat\textsf{D}$ 大调等。
- 关系大小调 调号相同的一组大小调。
- 平行大小调 主音相同的一组大小调。
和弦
我们首先讨论和弦的构成和命名。
传统的和弦是通过三度叠置来构建的。从根音开始往上叠两个三度,得到三和弦(中间音称作三音,最高音称作五音或者冠音)。在三和弦的基础上再叠一个三度,得到七和弦。
按照叠置的两个三度是大三度、小三度,三和弦可以命名为
| 构成 | 命名 |
|---|---|
| 大三度、小三度 | 大三和弦 |
| 小三度、大三度 | 小三和弦 |
| 大三度、大三度 | 增三和弦 |
| 小三度、小三度 | 减三和弦 |
注意增三和弦和减三和弦里面有增减五度,所以听起来可能很恶心,称作不协和和弦。其余称作协和和弦。
注意这时候为了强行符合三度叠置原则,你可能需要使用重升号和重降号,比如从 $\flat \textsf{G}$ 向上构成小三和弦,应当记作 $\{\flat \textsf{G}, \flat\flat\textsf{B}, \flat\textsf{D}\}$ 而非 $\{\flat \textsf{G}, \textsf{A}, \flat\textsf{D}\}$。
对于七和弦,将三和弦的名称和七度的名称组合起来构成其全名。
| 构成 | 名称 | 简称 |
|---|---|---|
| 减三和弦、小三度(减七度) | 减减七和弦 | 减七和弦 |
| 减三和弦、大三度(小七度) | 减小七和弦 | 半减七和弦 |
| 小三和弦、小三度(小七度) | 小小七和弦 | 小七和弦 |
| 小三和弦、大三度(大七度) | 小大七和弦 | |
| 大三和弦、小三度(小七度) | 大小七和弦 | 属七和弦 |
| 大三和弦、大三度(大七度) | 大大七和弦 | 大七和弦 |
| 增三和弦、小三度(大七度) | 增大七和弦 |
注意没有“增增七和弦”这一说,因为增七度和八度等音。
注意七度都是不协和音程,因此七和弦全是不协和和弦,但是作品中属七和弦、大七和弦、小七和弦、减七和弦、半减七和弦仍然常有出现。
和弦可以做转位,即将低音升高一个八度。
三和弦有原位和两种转位:以三音为低音的和弦称作第一转位和弦,因为低音和高音差六度,也称“六和弦”;以五音为低音的和弦称作第二转位和弦,因为低音和中音、高音依次相差四度、六度,也称为“四六和弦”。
七和弦有原位和三种转位,除第 $X$ 转位外,又分别可称作“五六和弦”、“三四和弦”、“二和弦”。你可以看出命名规律是标记低音和五音、七音的位置关系。
在调式音阶中,根音将获得一个编号。这样一来,每个三和弦将以如下规则获得一个和弦标记:
- 用罗马数字标注根音在调式音阶中的级数。大三和弦、增三和弦用大写字母,小三和弦、减三和弦用小写字母。增三和弦和减三和弦需额外加上标 $\square^\circ, \square^+$。
- 用下标 $\square_6, \square_{\begin{aligned}6 \\ 4\end{aligned}}$ 标注第一转位、第二转位。
接下来讨论和弦的调性功能。在调式的主音($\mathrm{I}$)、下属音($\mathrm{IV}$)、属音($\mathrm{V}$)上构成的和弦分别称作主和弦、下属和弦、属和弦,统称正和弦。
- 主和弦 给人以结束、完成的感觉,开始处和常用主和弦强调调性特征(“家”)。
- 属和弦 具有不稳定性,给人以进行到一半、尚未结束的感觉(“诗和远方”)。属七和弦可以进一步加强不稳定感。
- 下属和弦 具有衔接和过渡的作用。
下图是经典儿歌《我有一只小毛驴》中每小节的和弦:

可以发现和弦的连接方式有一些规律。一定范围内的和弦连接称作和声进行,正和弦之间有以下三种基本的方式:
- 正格进行 $\mathrm{I}\rightarrow \mathrm{V}\rightarrow\mathrm{I}$。
- 变格进行 $\mathrm{I}\rightarrow \mathrm{IV}\rightarrow\mathrm{I}$。
- 复式进行 $\mathrm{I}\rightarrow \mathrm{IV}\rightarrow \mathrm{V}\rightarrow\mathrm{I}$。
从不协和和弦连接协和和弦称作解决(resolution),在调性音乐中,所有和弦最终都要解决到 $\mathrm{I}$。
还有一些奇妙的和声进行,比如
《菊次郎的夏天》中

注意在和弦中你听的最清楚的是根音,这个分解和弦实际上省略了中音但是有类似的效果,其和声进行为:
$$
\mathrm{VI}\rightarrow \mathrm{V}\rightarrow \mathrm{IV}\rightarrow \mathrm{I}
$$瓦格纳 1865 年在歌剧《特里斯坦与伊索尔德》(Tristan und Isolde, WWV. 90)中展示了其对调性、和声结构的全新理解。他强调和弦本身的声音效果而非传统的和声功能。下谱是其前奏

开局即给出一个非常不稳定的阴间和弦,且剧中和弦进行始终没有解决,直到最后伊索尔德完成了“爱情之死”才终止于主三和弦。
布鲁斯音乐是在美国黑人音乐(劳动歌曲、灵歌等)的基础上发展出来的一种曲风。其和声进行很有特点。
标准的布鲁斯有十二个小节,分为三个乐句,基本和声进行为
$$
\begin{aligned}
\begin{matrix}
\mathrm{I} & \mathrm{I} & \mathrm{I} & \mathrm{I} \\
\mathrm{IV} & \mathrm{IV} & \mathrm{I} & \mathrm{I} \\
\mathrm{V} & \mathrm{IV} & \mathrm{I} & \mathrm{I} \\
\end{matrix}
\end{aligned}
$$因为是循环吟唱的,所以为了便于和声连接,将最后循环节的最后一小节改成 $\mathrm{V}$。
听了很多打着布鲁斯牌子的歌,但是水平太低没听出来和声进行,找半天找到一首:Ray Cooper Construction - Can’t wait no more,非常明显完全就是上面的规律。
卡农和弦:1 5 6 3 4 1 4 5 或者 1 5 6 3 4 1 2 5。

弦振动方程
这部分问题我们在 大作业 当中研究的很充分了。而且我这两天算数真的要算吐了,所以就不赘述了。这里重申 Marin Mersenne 定理和管乐器的分类是比较重要的,尤其注意同长度闭管的基频比开管低一个八度。下面补充一点我们没推到的东西,但是结果都抄书,这里也不算。
注意我们加了两个待定的傅里叶系数(在推式中为了形式简单,我们将傅里叶系数 $a_n, b_n$ 合并成了 $C_n, \phi_n$,这里需要拆开来看)。确定这两个系数还需要两个方程,可以采用下面的方式:
- 将弦的初始形状做奇延拓,从而可以确定一切 $\sin$ 的系数 $a_n$。
- 将弦的初始速度做奇延拓,假设解足够光滑,傅里叶级数可以逐项求导,可以得到一切 $\cos$ 的系数 $b_n$。
简单推导可以知道由静止开始拨弦则 $b_n$ 均为 $0$。
如果从弦正中央拨弦,要确定 $a_n$ 需要奇延拓并展开
$$
\phi(x) = \begin{cases}
2x / L & 0\leq x\leq L / 2 \\
2 - 2x / L & L/2\leq x\leq L
\end{cases}
$$
可以发现 $n$ 为偶数时傅里叶系数都是 $0$,这表明只有奇数倍基频的振动模态存在。读者可以自己实验在吉他的 12 品拨弦然后测量频谱,确实是这样的。
律学
真是狗屎大山。
要确定音级中每个元素对应的频率,可以从两个方面来看待:
- 绝对音高 确定每个音级的音高。
- 相对音高 确定一个八度内音级的音高。
首先绝对音高等于相对音高加确定一个音。国际上这个音正是此前提到的音乐会音高 $\textsf{A} = 440\text{ Hz}$。
三分损益、五度相生、纯律
凡将起五音凡首,先主一而三之,四开以合九九,以是生黄钟小素之首,以成宫。三分而益之以一,为百有八,为徵。不无有三分而去其乘,适足,以是生商。有三分,而复于其所,以是成羽。有三分,去其乘,适足,以是成角。
——《管子》地员篇
所谓三分益一,即将弦长乘 $1 + \frac 13$,三分损一即将弦长乘 $1 - \frac 13$。这段描述了如下生成宫商角徵羽五声音阶的方法:
- 取弦长为 $81$,记作宫音。
- 三分益一,即取弦长 $84\times 4/3 = 108$ 作为徵音。
- 三分损一,即取弦长 $108\times 2/3 = 72$,作为商音。
- 三分益一,即取弦长 $72\times 4/3 = 96$,作为羽音。
- 三分损一,即取弦长 $96\times 2/3 = 64$,作为角音。
将宫音定位中央 $\textsf{C}$,取商音、羽音的 $\frac 12$ 弦长得到和其同八度的音。注意 $2/3$ 和 $3/4$ 分别是理想中纯五度、纯四度的频率比,因此得到如下音级和弦长的对应关系:
| (徵) | (羽) | 宫 | 商 | 角 | 徵 | 羽 |
|---|---|---|---|---|---|---|
| $(108)$ | $(96)$ | $81$ | $72$ | $64$ | $54$ | $48$ |
| $(\textsf{G}’)$ | $(\textsf{A}’)$ | $\textsf{C}$ | $\textsf{D}$ | $\textsf{E}$ | $\textsf{G}$ | $\textsf{A}$ |
但是这样一来,音程 $\textsf{宫}-\textsf{角}$ 的比例为 $81 : 64$,略高于理想大三度的比例 $5:4$。
再做一轮三分益一、三分损一,又可以得到两个新音级,称为“变宫”和“变徵”,弦长分别为 $256/3$ 和 $512/9$。用减纯四度、加纯五度计算,变宫相当于 $\textsf{B}$,变徵相当于 $\sharp\textsf{F}$。这样得到的音阶称作雅乐音阶,或者古音阶。
我国古代亦有生成一个八度内十二个音级的办法,称为十二律,其名称和生律方法在《吕氏春秋》“季夏纪第六”中有所记载:
黄钟生林钟,林钟生太簇,太簇生南吕,南吕生姑洗,姑洗生应钟,应钟生蕤宾,蕤宾生大吕,大吕生夷则,夷则生夹钟,夹钟生无射,无射生仲吕。三分所生,益之一分以上生。三分所生,去其一分以下生。黄钟、大吕、太簇、夹钟、姑洗、仲吕、蕤宾为上,林钟、夷则、南吕、无射、应钟为下。
——《吕氏春秋》“季夏纪第六”
虽然文中指出了上生、下生的分布,但是没有总结其规律。事实上规律是默认做三分损一,如果发现弦长低于黄钟的二分之一,则乘二(做三分益一)。
那么对应关系是(弦长懒得写了)
| 黄钟 | 大吕 | 太簇 | 夹钟 | 姑洗 | 仲吕 | 蕤宾 | 林钟 | 夷则 | 南吕 | 无射 | 应钟 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| $\textsf{C}$ | $\sharp\textsf{C}$ | $\textsf{D}$ | $\sharp\textsf{D}$ | $\textsf{E}$ | $\textsf{F}$ | $\sharp\textsf{F}$ | $\textsf{G}$ | $\sharp\textsf{G}$ | $\textsf{A}$ | $\sharp\textsf{A}$ | $\textsf{B}$ |
| 宫 | 商 | 角 | 变徵 | 角 | 徵 | 变宫 |
Remark. 这顺序也是要背住的吗。。?
三分损益作为律制的问题在于“旋宫不归”,即取十二律最后一个被生成的元素仲吕再做三分损益,得到的是
$$
\frac{2^{18}}{3^{12}}\mathrm{len}(\textsf{C})\simeq 0.493270 \times \mathrm{len}(\textsf{C})
$$
并非比宫音低一个八度的音(清宫)。
在西汉时期,京房注意到了此问题,将仲吕再生之音命名为“执始”,并钻研发展六十律。
在西方也有一套类似的方法。毕达哥拉斯认为简单的整数比是优美的,$1:2$ 是八度,$2:3$ 是纯五度,$3:4$ 是纯四度。于是他选取 $3/2$ 作为生律元素,从 $\textsf{C}$ 的频率(不失一般性地记作 $1$)开始,每次乘 $3/2$,若超过 $2$,将其除 $2$ 来保证在一个八度内。
回忆十二律的生成和弦长与频率的关系,可以知道这和三分损益实际上就是一回事。那么也可以预见这样生律会出现和三分损益一样的问题:
纯五度和纯四度都是理想的,但是大三度音程频率比为 $81/64 > 5:4$。
从 $\sharp\textsf{E}$ 开始继续向上生律,得到一个频率为 $3^{12}/2^{18}$ 的音,这个音和理想的 $\textsf{C}’$ 之比为
$$
\frac{3^{12}}{2^{19}} = 1.013643
$$这称作毕达哥拉斯音差。
文艺复兴开始,西方音乐中越来越多重视三度、六度使用(猜测是为了三和弦?),于是考虑在五度相生法中添加一个生律元素:大三度($5:4$)。
从 $\textsf{C}$(频率为 $1$)出发,向上做大三度、纯四度、纯五度,可以确定 $\textsf{E}, \textsf{F}, \textsf{G}$,根据 $\textsf{E}-\textsf{A}$ 是大三度确定 $\textsf{A}$。然后用 $\textsf{B}-\textsf{E}$ 是纯五度确定 $\textsf{B}$,$\textsf{D}’-\textsf{G}$ 是纯五度确定 $\textsf{D}$。得到下表:
| $\textsf{C}$ | $\textsf{D}$ | $\textsf{E}$ | $\textsf{F}$ | $\textsf{G}$ | $\textsf{A}$ | $\textsf{B}$ | $\textsf{C}’$ |
|---|---|---|---|---|---|---|---|
| $1$ | $9/8$ | $5/4$ | $4/3$ | $3/2$ | $5/3$ | $15/8$ | $2$ |
这个生成过程非常强行,所以内部肯定有些一致性的问题:
- 纯五度 $\textsf{D}-\textsf{A}$ 不协和,比例为 $80/54$。
- 有两种不同的大二度(全音):$\textsf{C}-\textsf{D}$,$\textsf{F}-\textsf{G}$,$\textsf{A}-\textsf{B}$ 频率比为 $9/8$,$\textsf{D}-\textsf{E}$,$\textsf{G}-\textsf{A}$ 为 $10/9$。
- 全音和半音的不一致性直接导致了在这种方法生成的乐音体系上做转调是不可能的。
如果我们将“音差”问题理解为用生律元素生成元素但是没法回到原点的问题,那么纯律也有类似的问题:从 $\textsf{C}$ 出发,向上升高 $4$ 个纯五度(升高 $28$ 个半音),然后降低 $2$ 个八度和 $1$ 个大三度(降低 $28$ 个半音),频率为
$$
\left(\frac{3}{2}\right)^4\times \left(\frac 12\right)^2\times \frac 45 = \frac{81}{80} = 1.0125
$$
$1.0125$ 称为谐调音差。
中庸全音律、平均律
用简单有理数比进行生律必然产生音差,这是因为指望升高多个纯五度之后降低若干个八度能够回到原来位置,等价于求下面方程的正整数解:
$$
\left(\frac 32\right)^n = 2^m
$$
这等价于存在一个整数,能够被分解成 $3^n$ 和 $2^{n + m}$,这和算术基本定理是矛盾的。
但是可以尝试把音差均分给每个音程。16 世纪开始一些西方音乐理论家尝试在保持大三度和八度的前提下消除谐调音差,回忆谐调音差产生的方法是向上升高 $4$ 个纯五度,然后向下两个八度和一个大三度。因此我们希望纯五度的比例为
$$
x^4 \left(\frac 12\right)^2\times \frac 45 = 1 \quad \Rightarrow \quad x = \sqrt[4]{5}
$$
依次增加纯五度得到 $\textsf{C}\rightarrow\textsf{G}\rightarrow\textsf{D}\rightarrow\textsf{A}\rightarrow\textsf{E}\rightarrow\textsf{B}$,然后用 $\textsf{C}$ 减掉一个纯五度得到 $\textsf{F}$。这样的到了七个自然音级对应的频率
| $\textsf{C}$ | $\textsf{D}$ | $\textsf{E}$ | $\textsf{F}$ | $\textsf{G}$ | $\textsf{A}$ | $\textsf{B}$ | $\textsf{C}’$ |
|---|---|---|---|---|---|---|---|
| $1$ | $\sqrt 5/2$ | $5/4$ | $2\sqrt[4]{5^3}/5$ | $\sqrt[4]{5}$ | $\sqrt[4]{5^3}/2$ | $5\sqrt[4]{5}/4$ | $2$ |
注意到这样操作保住了所有的大三度,使得所有的大二度(全音)频率比都是 $\sqrt 5 / 2$,而这个数值正是纯律中两种大二度的几何平均值:
$$
\frac{\sqrt 5}{2} = \sqrt{\frac 98 \times \frac{10}{9}}
$$
总结起来中庸全音律:
- 消除了谐调音差。
- 全音音程和半音音程均一致。
- 大小三度、大小六度都和纯律一样,保持了纯律的效果。
- 可以在一定范围内转调。
- 但是五度听起来非常恶心($\sqrt[4]{5}\simeq 1.495349$)尤其是五度相生一直生成到 $\textsf{F}$,这个误差将累计 $10$ 次,最后和纯五度相去甚远。
最直接的办法就是将一个半音取作 $\sqrt[12]{2}$,这样的到的就是十二平均律。
这样的好处就是在保持了八度的前提下消除了一切音差,但是所有的音程都变垃圾了一些。
狗屎大山
可以用对数来将音程精确具象化。
定义 3.3.1(音分). 定义两声音频率为 $f_1 < f_2$,那么这两声音之间的音分数定义为:
$$
1200\log_2\left(\frac{f_2}{f_1}\right)
$$
这样一来十二平均律中一个半音的音分就是 $100$。人耳的分辨能力大概是 $4\sim 6$ 个音分,然后你发现非常不幸的是所有律制都有几个音程能被听出来区别。
在之前我们提到的乐理中狗屎大山产生的原因是希望纯五度和八度能够同时保持,即解方程
$$
\left(\frac{3}{2}\right)^n = 2^m
$$
两边取 $\log_2$ 得到这就是要求
$$
\log_2\left(\frac{3}{2}\right) = \frac{m}{n}
$$
然而我们知道左边不是一个有理数,所以这个方程没法解。然而众所周知,连分数逼近提供了无理数的最佳有理数近似:
定理 3.3.2(e.g. 任意一本初等数论教材) $A$ 为无理数,$p_N/q_N$ 为 $A$ 的连分数 $N$ 次渐进,那么对于任意的 $q\leq q_N$,都有
$$
\left\lvert A - \frac{p_N}{q_N}\right\rvert \leq \left\lvert A - \frac pq\right\rvert
$$
而简单计算 $\log_2(3/2)$ 的连分数逼近,得到:
$$
\log_2(3/2) = \frac{1}{1+\frac{1}{1+\frac{1}{1+\frac{1}{2+\frac{1}{2+\frac{1}{3+\frac{1}{1+\frac{1}{5+\cdots}}}}}}}}
$$
连分数逼近的前几项是
$$
1, \frac 12, \frac 35, \frac{7}{12}, \frac{24}{41}, \frac{31}{53}, \frac{179}{306}, \cdots
$$
这表明对于其中的 $p_N/q_N$,$q_N$-平均律中的纯五度都是理想纯五度的最佳近似。这一定程度上可以解释为什么东西方都不约而同地产生了 $12$ 声音阶。
机器作曲
这一节纯无聊。我们只记录一些零碎的观点。
音乐骰子游戏
1757 年克恩伯格出版《波洛涅兹和小步舞曲作曲常备》。
一段波洛涅兹舞曲有 $14$ 小节,克恩伯格为每小节写了 $11$ 种旋律,每次通过掷两个骰子将点数求和来随机选一段。
注意掷骰子求和得到的分布不是均匀的。
ILLIAC 组曲 1956 年到 1957 年美国作曲家 Lejaren Arthur Hiller 和化学家 Leonard M. Isaacson 在 ILLIAC I 计算机上用两个半八度中的 $31$ 个音级均匀随机生成了一首弦乐四重奏。
可以想象,这样均匀随机产生的东西很难有多好听。
因此也可以尝试从 Markov Chain 上采样出一段音乐。
这个 Markov Chain 可以从现有的音乐片段里面拟合。
用遗传算法来作曲。将两个小节中的音级编码成序列,那么除了遗传算法的两个经典操作:
- 交叉 交换两段序列中两个片段。
- 变异 随机改变一段序列中的一个音。
还可以加上针对音乐的特殊变异:移调、逆行、倒影等。
还需要确定估价函数,方法有:
- 根据音乐规律手动启发式构造估价函数。
- 用统计结果构造。
- 人机交互。
- 机器学习。
- ……
可以用机器学习来完成曲风分类、乐曲生成等。
音乐变换理论
音类空间和上方的变换
因为音名是八度循环的,所以我们取八度等价关系 $\sim$,然后做全体音级构成的集合 $\mathcal{P}$ 在此等价关系下的商集 $\mathcal{PC} = \mathcal{P} / \sim$,称作音类空间。显然 $\mathcal{PC}$ 和 $\mathbb{Z}_{12}$ 之间存在保相邻关系的一一对应。
对于一段旋律,直觉上有几种保持旋律性质的变换,如移调、倒影、逆行。移调和倒影单独作用在每个音上,严格地有:
- 移调变换 $T_n(\overline{x}) = \overline{x + n}$
- 倒影变换 $I(\overline{x}) = \overline{-x}$
简单计算可以知道 $T^k \circ I(\overline{x}) = \overline{k - x}$。
不难知道 $\langle T, I\rangle$ 同构于十二节二面体群 $D_{24}$。再加上 $R$,容易构造任意次移调和倒影都不能达到其回文的旋律,于是 $\langle T, I, R\rangle = \langle T, I\rangle\times \langle R\rangle$,为 $48$ 阶群。
注意这里的群元素都是对旋律的映射,运算是复合,检查映射的相等性使用外延性公理。
十二音技术
这一理论的贡献者是勋伯格。定义一个音列为十二个音列的一个排列。
做一个将音列的第一项映射到 $0$ 的 $\mathcal{PC}\rightarrow \mathbb{Z}_{12}$ 的保相邻关系的一一映射,就可以用 $[\overline{12}]$ 的一个排列来表示一个音列。
比如勋伯格的钢琴协奏曲 Concerto for piano and orchestra Op. 42 中有基本音列
$$
\flat\textsf{E},\flat\textsf{B}, \textsf{D}, \textsf{F}, \textsf{E}, \textsf{C}, \sharp\textsf{F},\flat\textsf{A}, \flat\textsf{D}, \textsf{A}, \textsf{B}, \textsf{G}
$$
可以记作
$$
0, 7, 11, 2, 1, 9, 3, 5, 10, 6, 8, 4
$$
初始音列记作 $P_0$。可以对音列做如下操作:
- 将每个元素升高 $k$ 个半音得到移调音列 $P_k$。
- 将 $P_k$ 关于 $P_k[0]$ 倒影,得到倒影音列 $I_k$。
- 将 $P_k$ 翻转(逆行)得到逆行音列 $R_k$。
- 将 $I_k$ 逆行得到逆行倒影音列 $RI_n$。
发现可能出现如下情况:初始音列中心对称。此时对于任意的 $I_k$ 总存在一个 $R_k$ 与其相等。此时一共只有 $24$ 条音列。其余情况下都有 $48$ 条音乐。
在使用十二音技术作曲时,音列给出的只是音列。具体采用哪个八度交由作曲家决定。
实际上用这种手法谱出的曲都很阴间。勋伯格的曲子在非专业人士听来如同乱弹。罗忠镕的《涉江采芙蓉》(依次呈现了 $P_0, R_0, I_0, RI_0$)听起来也非常阴间。
音类集合
$\mathcal{PC}$ 的一个 $n$ 元子集称作一个 $n$ 元 pc 集(音类集合)。
将音类集合标记在圆周上,得到一个内接 $n$ 边形。对于两个音类 $X, Y$,其距离定义为从圆周上从 $X$ 到 $Y$ 的最短路。比如 $\textsf{G}, \textsf{C}$ 之间的距离是 $5$,$\textsf{C}, \textsf{E}$ 之间的距离是 $4$。
记 $d_k$ 表示 pc 集中距离为 $k$ 的音类的无序对的数量,定义
$$
\delta = (d_1, d_2, d_3, d_4, d_5, d_6)
$$
为该 pc 集的距离向量,它给出了 pc 集的全部音程含量,从而刻画了该 pc 集的声音效果。
定理(共同音定理). 设音类集合 $\mathcal{X}$ 的距离向量是 $\delta$,那么当 $1\leq k\leq 5$ 时有 $|\mathcal{X}\cap T^k(\mathcal{X})| = |\mathcal{X}\cap T^{-k}(\mathcal{X})| = d_k$,当 $k = 6$ 时 $|\mathcal{X}\cap T^6(\mathcal{X})| = 2d_6$。
在特定的音乐语境中,只有少数子集合具有音乐上的意义。
音阶也是一种 pc 集。
如果将音阶画在五度圆周上,将会得到一段连续的弧。一个自然大调音阶的补恰好是一个五声音阶。
音网
这里的黎曼是音乐家 Hugo Riemann 而不是数学家 Bernhard Riemann。此理论中可以发现一些和声进行的规律。
将 $24$ 个大小三和弦(记作对应大 / 小写的根音,比如 $\textsf{G}$ 是以 $\textsf{G}$ 为根音的大三和弦)构成的集合称作 $\mathcal{S}$,在 $\mathcal{S}$ 上,我们定义:
- 平行变换 $P$,将一个三和弦变成其平行三和弦。(具有相同的根音的大三和弦和小三和弦称作平行三和弦,可以发现这两个和弦具有相同的纯五度音程)。
- 关系变换 $R$,将一个三和弦变成其关系三和弦。(具有相同的大三度音程的大三和弦和小三和弦称作关系三和弦)。
- 导音交换 $L$,将大三和弦的根音降低一个半音,或者将小三和弦的冠音升高一个半音。(将和弦打到与其具有相同小三度音程的和弦)
$P, R, L$ 称作黎曼变换。黎曼变换有直观的几何解释。将三和弦画在圆周上得到一个三角形,那么此三角形的边长为 $\overline{3}, \overline{4}, \overline{5}$($\overline{x}$ 表示弧长 $x$ 所对的弦长),这时
- $P$ 是关于 $\overline{5}$ 边中垂线的翻转。
- $R$ 是关于 $\overline{4}$ 边中垂线的翻转。
- $L$ 是关于 $\overline{3}$ 边中垂线的翻转。
从上文的论述中可以看出,做黎曼变换后两和弦之间有共同音程,于是可以实现平滑过渡。比如贝多芬第九交响曲第二乐章·谐谑曲的弦乐组第 $143-146$ 小节,和弦进行为
$$
\textsf{C}\xrightarrow{R} a\xrightarrow{L} F \xrightarrow{R} d
$$
欧拉在著作《音乐新理论探索》中给出了如下的音网:
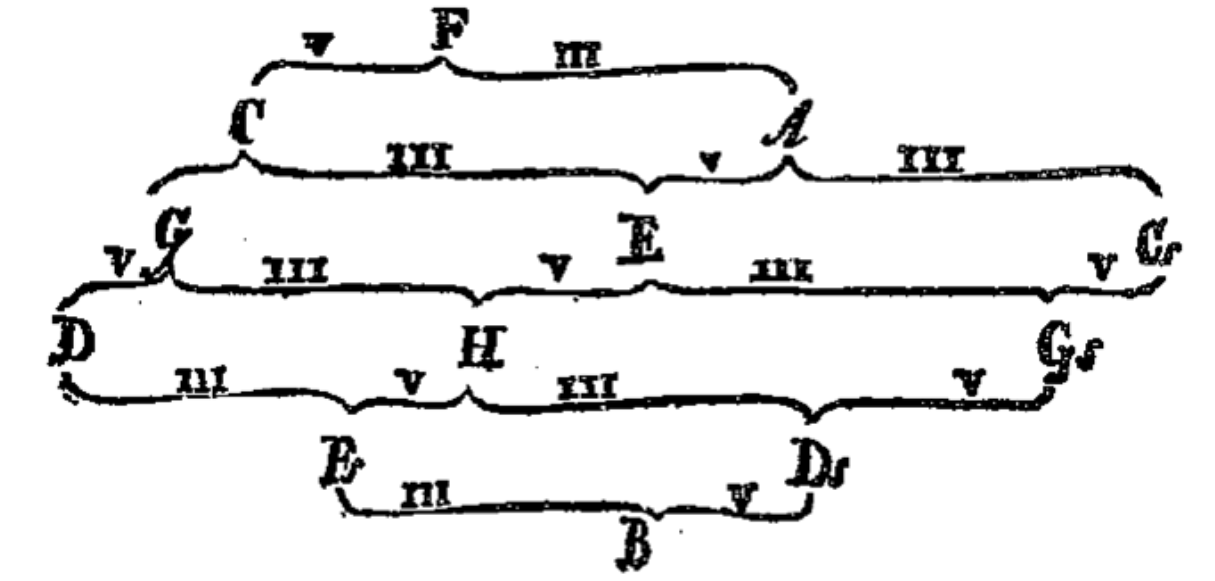
此网上的边都是大三度或者纯五度音程。
接下来我们来推导另一种音网。从某大三和弦出发,依次作用 $P, R, L, P, R, L$,可以得到一个循环
$$
C\xrightarrow{P} c \xrightarrow{R} \flat E \xrightarrow{L} g \xrightarrow{P} G \xrightarrow{R} e \xrightarrow{L} C
$$
注意到每个循环上所有和弦都包含一个唯一的音类(上面的循环中共同的音类是 $\textsf{G}$)。从每个音类出发,一共可以做出 $12$ 个六边形,每个循环可以排成一个正六边形。将所有正六边形的公共边重合,得到一张无限延申的网:
注意网上 | 方向两六边形包含的共同音类是大三度,/ 方向是纯五度,\ 方向是小三度。因此做此图的对偶图,得到的就是纯五度、大三度、小三度音程织成的音网。欧拉的音网正是其生成子图。
新黎曼理论
将三个黎曼变换在复合运算上构成的群
$$
\mathcal{N} = \langle P, R, L\rangle
$$
称作新黎曼群。
观察上面的图,可以发现我用蓝色线框出来的两个序列都是五度循环,于是可以发现 $R\circ L$ 相当于二面体旋转,$P$ 相当于二面体翻转。而
- $P = P$。
- $R = P\circ(R\circ L)^{-2}$。
- $L = R^{-1}\circ (R\circ L)$。
$R\circ L$ 和 $P$ 组成 $\mathcal{N}$ 的生成元,所以 $P$ 同构于十二阶正二面体群 $D_{2n}$。
注意到依次作用 $R$, $L$, $R$, $L$, …… 可以平滑地遍历全体三和弦。
零散音乐史
早期音乐是单声部音乐。
公元九世纪前后出现的奥尔加农是多声部音乐的雏形。
多声部音乐可以分为
- 复调音乐:不同声部相对独立,按照对位法结合。
- 主调音乐:一个旋律为主要旋律声部,其他缺少独立性。
赋格:一种盛行于巴洛克时期的复调音乐题材。乐曲开始时,以单声部形式贯穿全曲的主要音乐素材称为”主题”,与主题形成对位关系的称为”对题”。分为呈示部、展开部、再现部。
里切卡尔:“无插部赋格”
纯律的主要倡导者是意大利音乐理论家扎利诺(?ref:https://www.daowen.com/lilun/2141127.html)
明代律学家朱载堉最早计算出十二平均律关键数字 $\sqrt[12] 2$,称作“密律”。