关于管乐器泛音演奏(超吹)的一些探究
Abstract. 本文是 2024 秋季学期音乐与数学大作业的笔记,研究题目是“管乐器的超吹”,尤其是为何开管乐器能够吹出偶数倍泛音,闭管乐器只能够吹出奇数倍泛音,而锥形管乐器看似和闭管相同,但实际上也能吹出偶数倍泛音。对管乐器的分类参见第 3,第 4 节。
警告: 本文可能包含如下要素:
- 随便忽略高阶小量。
- 随便使用对称性。
- 随便交换微分算子。
- 对着参考文献人云亦云。
如您无法接受这些操作,我们推荐您不要阅读此文。
前置知识:声波的线性波动方程
在本节中我们推到声音传播时,压强满足的偏微分方程。在自然中,这个方程是非线性的。但是实践中,其线性近似足够解决问题。
记号. 我们约定如下记号:
- 位置 $\boldsymbol{r} = x\boldsymbol{x} + y\boldsymbol{y} + z\boldsymbol{z}$。
- 粒子位移 $\boldsymbol{\xi} = \xi_x\boldsymbol{x} + \xi_y\boldsymbol{y} + \xi_z\boldsymbol{z}$。
- 粒子速度 $\boldsymbol{u} = \dfrac{\partial \boldsymbol{\xi}}{\partial t}$。
- 密度 $\rho$。
- 压缩比 $s = \dfrac{\rho - \rho_0}{\rho_0}$
- 声压 $p = P - P_0$。
其中带有下标 $\square_0$ 的量表示平衡态下该物理量的值。对应的不加角标的记号表示扰动后实际上的值,都是关于时间和坐标的函数。
可以发现描述这个系统涉及到三种物理量(位置、密度、压强,及其若干阶导数),推出波动方程的过程中我们需要用到三个中间结果,依次称为
- 气体状态方程 联系压强和密度。
- 连续性方程 本质上是质量守恒,联系粒子速度和密度。
- 动力学方程 联系粒子速度和压强。
该方程的最终形式在 \ref{acousticeq} 中给出,在文献 [1] 等当中也有相同的形式。
气体状态方程
回忆在准静态过程中,气体的压强和密度总是满足一定的关系,比如:
$$
\frac{P}{P_0} = \frac{\rho}{\rho_0} \quad {\color{blue}\text{(isothermic)}} \qquad \text{or} \qquad \frac{P}{P_0} = \left(\frac{\rho}{\rho_0}\right)^\gamma \quad {\color{blue}\text{(adiabat)}}
$$
其中 $\gamma$ 是热容比 $C_p / C_v$。从方程中抽出 $P, \rho$ 之间的函数关系,然后将 $P$ 在 $\rho_0$ 处展开成 $\rho$ 的泰勒级数
$$
P = P_{\rho_0} + \left(\frac{\partial P}{\partial \rho}\right)_{\rho_0}(\rho - \rho_0) + O((\rho - \rho_0)^2)
$$
定义下面的常量为气体的体积模量
$$
\mathbf{B} = \rho_0\left(\frac{\partial P}{\partial \rho}\right)_{\rho_0}
$$
那么在仅施加微扰的情况下($s\ll 1$)我们得到了下面的气体状态方程:
$$
\boxed{p = \mathbf{B} s} \label{stateeq}
$$
连续性方程
这一段推导基于如下假设:固定 $t$,$\xi$ 是一个关于 $x$ 的连续函数。
我们先从一个维度上来推导,然后推广到高维。同样,我们假设只有微扰,即 $\lvert\nabla \xi\rvert \ll 1$。那么感性理解起来
$$
(x + \Delta x)(y + \Delta y)(z + \Delta z) - xyz = yz\Delta x + xz\Delta y + xy\Delta z + o(1)
$$
一个空间体元的体积变化量近似是三个维度上的变化量的加和。
考虑一个垂直于 $x$ 轴的、面积为 $A$ 的小截面。此截面上 $[x, x + \Delta x]$ 这一段气体分子实际上的位置是 $[x + \xi_x(x), x + \Delta x + \xi_x(x + \Delta x)]$,那么 $x$ 轴方向对体积变化的贡献为
$$
A(\xi_x(x + \Delta x, t) - \xi_x(x, t)) \simeq A\frac{\partial \xi_x}{\partial x}\Delta x
$$
注意 $A\Delta x$ 实际上就是体元原来的体积 $\Delta V$。于是该体元的体积变化量就是
$$
(\Delta V) \nabla \cdot \boldsymbol{\xi}
$$
由于质量是守恒的,有
$$
\rho_0 \Delta V = \rho \Delta V (1 + \nabla \cdot \boldsymbol{\xi})
$$
即得到
$$
\rho_0 - \rho = \rho \nabla \cdot \boldsymbol{\xi}
$$
两边对时间求导得到
$$
\frac{\partial \rho}{\partial t} = {\color{orange}-\frac{\partial \rho}{\partial t} \nabla \cdot \boldsymbol{\xi}} - \rho \nabla \cdot \frac{\partial \boldsymbol{\xi}}{\partial t}
$$
注意前面高亮的一项实际上是一个比 $\partial \rho / \partial t$ 高阶的小量,而 $\rho$ 可以近似等于 $\rho_0$(这个近似是为了将方程线性化),于是我们得到了下面的方程:
$$
\boxed{\frac{\partial \rho}{\partial t} = - \rho_0 \nabla \cdot \boldsymbol{u}} \label{masseq}
$$
动力学方程
取体元 $\Delta V$,考虑 $x$ 方向上的分量,有
$$
f_x = -\frac{\partial p}{\partial x}\mathrm{d}V
$$
将所有分量综合起来
$$
\boldsymbol{f} = -(\nabla p)\mathrm{d}V
$$
根据牛顿第二定律
$$
\boldsymbol{f} = \boldsymbol{a}\rho\mathrm{d}V
$$
其中 $\boldsymbol{a} = \mathrm{d}\boldsymbol{u} / \mathrm{d}t$,这与 $\partial \boldsymbol{u} / \partial t$ 之间存在细微的差距,因为粒子的位置也在发生变化。所以这里原本需要计算一个全微分:
$$
\begin{align}
\boldsymbol{a} &= \left(\frac{\mathrm{d}\boldsymbol{u}}{\mathrm{d}x}\frac{\partial x}{\partial t} + \frac{\mathrm{d}\boldsymbol{u}}{\mathrm{d}y}\frac{\partial y}{\partial t} + \frac{\mathrm{d}\boldsymbol{u}}{\mathrm{d}z}\frac{\partial z}{\partial t} + \frac{\partial \boldsymbol{u}}{\partial t}\right) \\
&= (\boldsymbol{u}\cdot\nabla)\boldsymbol{u} + \frac{\partial \boldsymbol{u}}{\partial t}
\end{align}
$$
但是不知道为什么就把第一项近似掉了(似乎是认为在微扰的假设下粒子速度和局部速度差都是小量)。总之我们得到了
$$
-\nabla p = \rho\frac{\partial \boldsymbol{u}}{\partial t}
$$
这个方程仍然是非线性的,于是我们把 $\rho$ 近似成 $\rho_0$。
$$
\boxed{-\nabla p = \rho_0\frac{\partial \boldsymbol{u}}{\partial t}} \label{forceeq}
$$
我们将上述方程联立起来的到 $p$ 的波动方程。首先对气体状态方程 \ref{stateeq} 求时间的偏导得到
$$
\frac{\partial p}{\partial t} = \frac{\mathbf{B}}{\rho_0}\frac{\partial \rho}{\partial t}
$$
将其带入连续性方程 \ref{masseq} 中得到
$$
\frac{\rho_0}{\mathbf{B}}\frac{\partial p}{\partial t} = -\rho_0\nabla \cdot\boldsymbol{u}
$$
上式中两边对 $t$ 求偏导,将动力学方程 \ref{forceeq} 两边作用 $(\nabla \cdot)$ 后可以消掉 $u$,得到
$$
\boxed{\frac{\mathbf{B}}{\rho_0} \nabla^2 p = \frac{\partial p}{\partial t^2}} \label{acousticeq}
$$
这称为声波的线性波动方程。此方程和电磁波等的波动方程具有相同的形式。
从拨弦的情形入手 d’Alembert 定理
本节是《音乐与数学》课程内容的拓展,详细给出了弦振动方程的解法。
设弦张力为 $T$,线密度为 $\rho$。取一段微元 $\Delta x$ 做受力分析。以向上为正方向设这段微元的位移为 $y(x, t)$。
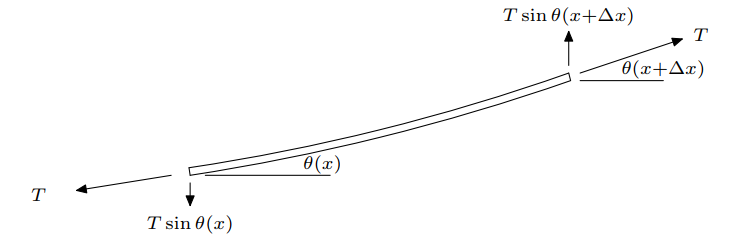
在 $\theta$ 很小的情况下可以用 $\partial y / \partial x$ 近似 $\sin(x)$。于是依照牛顿定律得到方程
$$
T\left(\frac{\partial y}{\partial x}(x + \Delta x) - \frac{\partial y}{\partial x}(x)\right) = \rho\Delta x \frac{\partial^2 y}{\partial t^2}
$$
令 $\Delta x\rightarrow 0$,得到偏微分方程(其中 $c = \sqrt{T / \rho}$)
定义 1.1(弦振动方程) 给定张力为 $T$,线密度为 $\rho$ 的弦。定义 $c = \sqrt{T / \rho}$,则
$$
\boxed{c^2\frac{\partial^2 y}{\partial x^2} = \frac{\partial^2 y}{\partial t^2}} \label{stringvibr}
$$
可以发现此方程就是空气振动方程退化到一维。
由于弦两端锁死,所以方程包含边值条件 $y(0, t) = y(L, t) = 0$。现在解该方程,首先假设一切函数都足够光滑,那么偏导算子是对易的,这就是说
$$
\left(\frac{\partial}{\partial t} + c\frac{\partial}{\partial x}\right)\left(\frac{\partial}{\partial t} - c\frac{\partial}{\partial x}\right)y = 0
$$
设 $u = x + ct, v = x - ct$,那么根据链式法则
$$
\begin{cases}
\dfrac{\partial}{\partial x} = \dfrac{\partial}{\partial u}\dfrac{\partial u}{\partial x} + \dfrac{\partial}{\partial v}\dfrac{\partial v}{\partial x} = \dfrac{\partial}{\partial u} + \dfrac{\partial}{\partial v} \\
\dfrac{\partial}{\partial t} = \dfrac{\partial}{\partial u}\dfrac{\partial u}{\partial t} + \dfrac{\partial}{\partial v}\dfrac{\partial v}{\partial t} = c\left(\dfrac{\partial}{\partial u} - \dfrac{\partial}{\partial v}\right)
\end{cases}
$$
带入上式之后整理得到
$$
{\color{grey} 4c^2}\frac{\partial^2}{\partial u\partial v}y = 0
$$
这表明方程的通解是 $y = f(x + ct) + g(x - ct)$。从几何上理解,这是两列依次从右往左和从左往右以速度 $c$ 传播的行波的叠加,这也是为什么这个解称作原方程的行波解。现在加上边值条件得到
$$
\begin{cases}
f(ct) + g(-ct) = 0 \\
f(L + ct) + g(L - ct) = 0
\end{cases}
$$
于是答案改写为
$$
y = f(ct + x) - f(ct - x)
$$
置 $ct = \lambda$(显然可以取到任意的实数)$f(\lambda - L) = f(\lambda + L)$,这表明原微分方程的解都是周期解。综上,我们得到了如下定理
定理 1.2(d’Alembert). 弦振动方程 $\ref{stringvibr}$ 附上边值条件的通解是
$$
y(x, t) = f(ct + x) - f(ct - x)
$$
其中 $f$ 是周期为 $2L$ 的函数。
将 $f(x)$ 其展开成傅里叶级数,$\sin$ 和 $\cos$ 用辅助角公式合并成 $\cos$,系数均作待定系数,得到
$$
f(x) = \sum_{n=1}^{\infty} C_n \cos\left(\frac{n\pi x}{L} + \phi_n\right)
$$
换回原来的式子中和差化积得到
$$
y = \sum_{n=1}^\infty 2C_n\sin\left(\frac{n\pi x}{L}\right)\sin\left(\frac{n\pi ct}{L} + \phi_n\right)
$$
单独考察横坐标为 $x$ 的振动模态,观察到它是无穷多个简谐振动的叠加,其第 $i$ 个振动振幅为 $2C_n\sin\left(\frac{n\pi x}{L}\right)$,频率为 $\frac{nc}{2L}$,这给出了如下结果:
定理 1.3(Marin Mersenne). 一根弦张力为 $T$,线密度为 $\rho$,长度为 $L$,那么拨弦产生的声音的基音频率为
$$
\frac{1}{2L}\sqrt{\frac{T}{\rho}}
$$
第 $n$ 泛音的频率为
$$
\frac{n + 1}{2L}\sqrt{\frac{T}{\rho}}
$$
现在要决定每个振动的强度,还需要确定待定系数 $C_n$。这时只需要对初状态做傅里叶分析即可。因为不是我们讨论的重点,所以略去。
柱形管乐器的振动方程解
在乐器有柱对称性时,我们做柱坐标换元,此时 Laplace 算子形式为
$$
\nabla^2 = \frac{\partial^2}{\partial \rho^2} + \frac{1}{\rho}\frac{\partial}{\partial \rho} + \frac{1}{\rho^2}\frac{\partial^2}{\partial \theta^2} + \frac{\partial^2}{\partial z^2}
$$
我们认为乐器为柱对称时,方程的解应当也满足柱对称性,即一切和 $\rho, \theta$ 有关的偏导均为 $0$。此时方程简化为
$$
c^2\frac{\partial^2 p}{\partial z^2} = \frac{\partial^2 p}{\partial t^2}
$$
于是此方程可以得到和弦振动方程一样的行波解。
为了给出方程的解,我们需要加边值条件。然而此处的边值条件和管的形状有关,根据一些参考文献:
开管(一端为送气口,一端敞开),则两端都有边值条件 $p = 0$(与大气相通)。
长笛、竖笛等属于此类。
I 类闭管(一端为送气口,一段封闭),则送气端有边值条件 $p = 0$(与大气相通),封闭端有边值条件 $\partial p / \partial x = 0$(这一段的粒子不能移动,受合力为 $0$)。
一种非主流的乐器,称作“滑哨笛”或者“溜溜笛”是此类的实例。
II 类闭管(一端为哨口,一段敞开),注意哨口可以近似认为是闭口。
此外,对于敞开口,可能实际参与振动的空气柱长度(称作有效长度)大于物理的管长,因此计算中可能需要求这个有效长度(称作管口校正)。下文中我们暂时忽略管口校正。
开管施加边值条件后得到的边值问题和弦振动的情形别无二致,因此一切结论都保留。现在考虑闭管的情形。首先有行波解
$$
p(x, t) = f(ct + x) + g(x - ct)
$$
`
和边值条件:
$$
\begin{cases}
\dfrac{\partial}{\partial x} p(0, t) \equiv 0 & \Rightarrow f’(\lambda) + g’(-\lambda) = 0 \\
p(L, t) \equiv 0 & \Rightarrow f(ct + L) + g(L - ct) = 0
\end{cases}
$$
将第一个关系从 $0$ 积分到 $\lambda$ 立即得到 $f(\lambda) = g(-\lambda) + C$,带进第二个关系当中得到 $f(\lambda + L) + f(\lambda - L) = C$。对此式子稍做操作:
$$
f(u) + f(u + 2L) = C, f(u + 2L) + f(u + 4L) = C \quad \Rightarrow \quad f(u) = f(u + 4L)
$$
至少说明所有的解都是周期解,只是周期变成了 $4L$。现在套上上文的傅里叶分析,得到解具有形式
$$
\xi(x, t) = \sum_{i=1}^\infty 2C_n\cos\left(\frac{n\pi x}{2L}\right)\cos\left(\frac{n\pi ct}{2L} + \phi_n\right)
$$
进一步分析,因为在 $x = L$ 处有 $p(x, t)\equiv 0$,因此我们对上述函数代入 $x = L$ 得到
$$
0(t) = \sum_{n=1}^\infty 2C_n\cos\left(\frac{n\pi}{2}\right)\cos\left(\frac{n\pi ct}{2L} + \phi_n\right)
$$
注意任意函数在傅里叶基下的坐标唯一,而 $0(t)$ 的一个坐标为 $(0, 0, …)$,因此有当 $n$ 为偶数时,必须有 $C_n = 0$。所以解一定具有形式
$$
p(x, t) = \sum_{n=1, \text{$n$ is odd}}^\infty 2C_n\cos\left(\frac{n\pi x}{2L}\right)\cos\left(\frac{n\pi ct}{2L} + \phi_n\right)
$$
这表明闭管乐器的基频为
$$
\frac{1}{4L}\cdot c
$$
比开管乐器低一个八度,并且只能够吹奏奇数阶泛音,符合我们的常识。
锥形管乐器的振动方程解
现在我们考虑一类锥形的管乐器,如双簧管、萨克斯、唢呐。此类乐器的哨片和 II 类闭管乐器完全一致,但是实践中此类乐器能够超吹出偶数次泛音。在文献 [3] 和其他一些文献中,作者宣称锥形管等效于同长度的开管,但没有给出推导。文献 [4] 给出了一种理论上的推导。
我们尝试给这一反直觉现象给出解释。
我们认为,这种乐器具有球对称性。此时我们做球坐标换元,Laplace 算子的形式为
$$
\nabla^2 = \frac{\partial^2}{\partial r^2} + \frac{2}{r}\frac{\partial}{\partial r} + \frac{1}{r^2}\left(\frac{\partial^2}{\partial \theta^2} + \cot\theta\frac{\partial}{\partial \theta} + \csc ^2\theta\frac{\partial^2}{\partial \varphi^2}\right)
$$
在具有球对称性时,和 $\theta, \varphi$ 有关的偏导均为 $0$。此时方程简化为
$$
c^2\left(\frac{\partial^2}{\partial r^2} + \frac{2}{r}\frac{\partial}{\partial r}\right)p = \frac{\partial^2 p}{\partial t^2}
$$
注意到
$$
\left(r\frac{\partial^2}{\partial r^2}p + 2\frac{\partial}{\partial r}p\right) = \left(r\frac{\partial^2}{\partial r^2}p + 2\frac{\partial}{\partial r}r\frac{\partial}{\partial r}p + \frac{\partial^2}{\partial r^2}r p\right) = \frac{\partial}{\partial r^2}(rp)
$$
所以置 $q = rp$,立即得到方程
$$
c^2\frac{\partial^2}{\partial r^2}q = \frac{\partial^2}{\partial t^2} q \label{coniceq}
$$
若假设 $p$ 是一个有界的量,那么无论是在左端还是右端,都有 $rp = 0$。于是 \ref{coniceq} 的边值问题和开管乐器完全一致。在得到的解中,除开奇异的端点不方便分析,其余的点确实可能产生频率为偶数倍基频的振动模态。
参考文献
[1] Joshua E. Greenspon, Acoustics, Linear, Encyclopedia of Physical Science and Technology (Third Edition), 2003
[2] Neville H. Fletcher, Thomas D. Rossing, The Physics of Musical Instruments, Springer (1991)
[3] Dave Benson, Music: A Mathematical Offering, 1995.
[4] R. Dean Ayers, Lowell J. Eliason and Daniel Mahgerefteh, The conical bore in musical acoustics, Amer. J. Physics 53 (6) (1985), 528–537.