Revision | 量子计算

Abstract.

• 基础与概览
  • 量子门通用性
  • 基础算法
• 基于量子傅里叶变换的算法
  • 量子相位估计
  • 求元素的阶
  • Shor 算法
• 基于 $SU(2)$ 旋转的量子算法
  • Grover
  • Quantum Random Walk
    • Quantum Random Walk 中的旋转变换
    • 判断完全图中是否有标记
    • 元素区分问题
• 基于 Hamiltonian 模拟的算法
  • 乘积公式
  • 稀疏 Hamiltonian 模拟
  • 连续时间量子游走

基础与概览

量子门通用性

对于经典电路，称一个门的集合是通用的，若其能够计算一切布尔函数 $f : {0, 1}^n\rightarrow {0, 1}^m$。我们熟知 ${\mathrm{NAND}}, {\mathrm{AND}, \mathrm{NOT}}$ 都是通用的。（需要指出的是，在经典计算中，我们默认可以使用复制输出的 FAN-OUT 门）。

下面的门称作 Toffoli 门

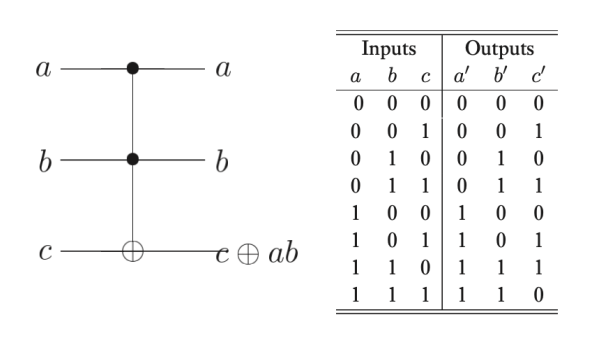
容易发现 Toffoli 门可以制作经典 NAND 门和 FAN-OUT 门，因此 Toffoli 门是通用的。此外注意到 Toffoli 门作用两次相当于什么都没发生，因此 Toffoli 门是可逆的。现在使用 Toffoli 门，我们可以计算一切布尔函数，输入 $x_1, …, x_n$，结果为 $y_1, …, y_m$，但是需要引入若干初始为 $0$ 的辅助比特，这些辅助比特在经过电路之后变成了 $j_1, …, j_k$，那么可以通过如下变换来消除掉辅助比特：

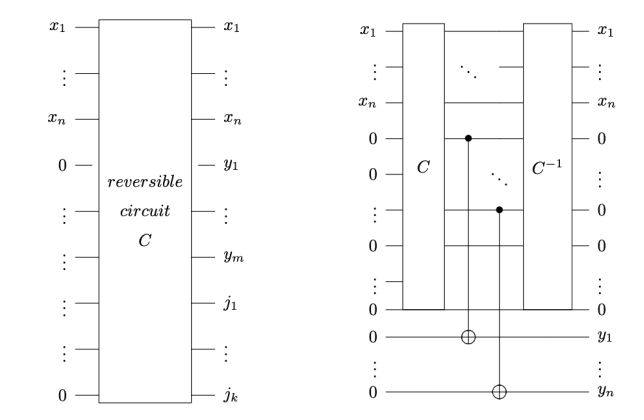
命题 1.1.1. 一切布尔函数都可以用 Toffoli Gate 配上若干初始和结尾都为 $0$ 的辅助比特来计算。

在量子线路中我们接受这些单、双量子比特门：

• Pauli $X, Y, Z$ 门
  $$
  X = \begin{pmatrix}
  0 & 1 \\
  1 & 0
  \end{pmatrix} \quad Y = \begin{pmatrix}
  0 & -i \\
  i & 0
  \end{pmatrix} \quad Z = \begin{pmatrix}
  1 & 0 \\
  0 & -1
  \end{pmatrix}
  $$
  及其拓展版本 $R_X(\theta) = \exp\left(-i\frac\theta 2 X\right)， R_Y(\theta) = \exp\left(-i\frac\theta 2 Y\right)， R_Y(\theta) = \exp\left(-i\frac\theta 2 Y\right)$。

• Hadamard 门，$S$ 门，$T$ 门。
  $$
  H = \frac 1{\sqrt 2}\begin{pmatrix}1& 1 \\
  1 &-1\end{pmatrix}\quad S = \begin{pmatrix}1& 0\\
  0 &i\end{pmatrix}\quad T = \begin{pmatrix}1& 0 \\
  0 &e^{i\frac \pi4}\end{pmatrix}
  $$

• 受控 $U$ 门：$\textsf c!-!U = \ket 0\bra 0 \otimes I + \ket 1\bra 1\otimes U$，一个特例是 CNOT 门（$\mathrm{CNOT} = \ket 0\bra 0 \otimes I + \ket 1 \bra 1 \otimes X$）。

有时也可以使用 Toffoli 门。

注意一个态总是可以表示成（忽略全局相位）
$$
\ket\psi = \cos \frac \theta 2\ket 0 + e^{i\phi} \sin \frac \theta 2\ket 1
$$
以 $\phi, \theta$ 作为球坐标，可以将一个态画在一个单位球面（Bloch Sphere）上。经过一些琐碎的讨论，可以证明对于 $\hat n= (n_x, n_y, n_z)\in \mathbb{S}^3$（$\mathbb S^3$ 指三维欧几里得空间中的单位球面），下面形式的酉变换：
$$
R_{\hat n}(\theta) = e^{i\frac \theta 2(n_x X + n_yY + n_zZ)}
$$
是球面上绕 $\hat n$ 旋转 $\theta$ 度。接下来我们证明如下结论：

命题 1.1.2. 任何的 $1$-qubit 门都可以被分解为
$$
e^{i\phi}R_z(\theta_3)R_x(\theta_2)R_z(\theta_1)
$$
其中 $\phi, \theta_1, \theta_2, \theta_3\in \R$。

证明. 所有的 $1$-qubit 门都是酉变换，而任意的酉变换 $U$ 都可以对角化，其特征值全为模长为 $1$ 的复数：
$$
U = P^\dagger{\rm diag}(e^{i\theta_1}, e^{i\theta_2})P = \exp\left(iP^\dagger {\rm diag}(\theta_1, \theta_2)P\right)
$$
注意 $P^\dagger {\rm diag}(\theta_1, \theta_2)P$ 是 Hermit 矩阵，而 Pauli 矩阵 $I, X, Y, Z$ 是二阶 Hermit 矩阵的一组基，所以存在实数 $c_1, c_2, c_3, c_4$ 使得
$$
P^\dagger {\rm diag}(\theta_1, \theta_2)P = c_1I + c_2X + c_3Y + c_4 Z
$$
若 $c_2, c_3, c_4 = 0$，那么该酉变换就是一个全局相位。于是不妨设 $c_2^2 + c_3^2 + c_4^2 = (2 / \theta)^2 > 0$。令 $n_x = c_2 / (\theta / 2), n_y = c_3 / (\theta / 2), n_z = c_4 / (\theta / 2)$。则
$$
U = \exp\left(ic_1 I + i\frac\theta 2(n_xX + n_yY + n_zZ)\right)
$$
注意 $I$ 和一切矩阵对易，所以 $U = e^{ic_1}R_{\hat n}(\theta)$。只需要验证一切三维空间中的旋转都可以拆分成一次绕 $z$ 轴的旋转，一次绕 $x$ 轴的旋转，一次绕 $z$ 轴的旋转即可。

这个很符合直觉，而且我也有一个几何证明（但是太丑了不想放上来），所以我不写证明。

接下来讨论量子门的通用性。然而因为系数非常复杂，恐怕不能用有限的门集合精确实现一切酉变换。因此我们定义一个度量：
$$
E(U, V) = \max_{\ket \psi} \left\lVert U\ket \psi - V\ket \psi \right\rVert
$$
称一个量子门的集合是通用的，若对于任意的正整数 $n$，$n$-qubit 酉变换 $U$ 和 $\varepsilon > 0$，都存在一个序列 $V_1, V_2, …, V_k$，使得该门被 $\varepsilon$-近似，即
$$
E(U, V_1\cdots V_k) \leq \varepsilon
$$

• 经典 Toffoli 门是通用的，但是在量子计算下，它无法把 $\ket 0^{\otimes n}$ 映射到纠缠态。
• ${\mathrm{CNOT}, X, Y, Z}$ 也不是通用的，它也不能把 $\ket 0^{\otimes n}$ 映射到纠缠态。

下面的结论证明都超出了能力范围。

命题 1.1.3. 通用的 $1$-qubit 门集合并上产生纠缠态的门集合得到通用的门集合。

${\mathrm{CNOT}, H, T}$ 是完备的。因为 $HTHT, THTH$ 给出了无理数旋转角，而 $\mathrm{CNOT}, H$ 可以产生纠缠态。

定理 1.1.4 (Solovay-Kitaev). 给定一个在求逆下封闭的通用的 $1$-qubit 门的集合，任意的 $1$-qubit 门都可以用 $O(\log^4(1/\varepsilon))$ 个该集合中的门 $\varepsilon$-近似。

这个指数现在被优化到了 $1.44043$。

基础算法

首先定义 Bell 基：
$$
\ket{\beta_{zx}} = ((Z^zX^x)\otimes I)\frac 12(\ket{00} + \ket{11})
$$
容易验证这是一组标准正交基。

量子超密编码

Alice 和 Bob 共享一个纠缠态 $\ket{\beta_{00}}$。那么 Alice 可以给 Bob 发送一个 qubit 来使 Bob 获得两个经典 bit 的信息。

假设 Alice 想要发送 $zx\in{0, 1}^2$，那么：

• Alice 在她的 qubit 上作用 $Z^zX^x$。
• Alice 把她的 qubit 发送给 Bob。
• Bob 在贝尔基下测量，立即知道 Alice 作用了什么酉变换，从而知道 Alice 要发送的经典 bit。

量子隐形传态

Alice 和 Bob 共享一个纠缠态 $\ket{\beta_{00}}$，Alice 手里有一个态 $\ket\psi$，那么 Alice 可以给 Bob 发送两个经典 bit 来把 $\ket\psi$ 发送给 Bob。

考虑如下过程：

• Alice 在 Bell 基下测量自己手里的两个 qubit，得到 $\beta_{zx}$。
• Alice 发送 $z, x$ 给 Bob。
• Bob 在他的 qubit 上作用 $Z^zX^x$。

我们计算这个过程中，整个系统会发生了什么。这是一个三量子比特的系统，简单计算发现
$$
\begin{aligned}
\ket \psi\ket{\beta_{00}} &= (a_0\ket 0 + a_1\ket 1)\frac 1{\sqrt 2}(\ket{00} + \ket{11}) \\
&= \frac 1{\sqrt 2}(a_0\ket{00}\ket 0 + a_1\ket{10}\ket 0 + a_0\ket{01}\ket 1 + a_1\ket{11}\ket 1) \\
&= \frac{1}{2}(\ket{\beta_{00}}\ket\psi + \ket{\beta_{01}}X\ket\psi + \ket{\beta_{10}}Z\ket\psi + \ket{\beta_{11}}XZ\ket\psi)
\end{aligned}
$$
所以如果 Alice 测量得到了 $\beta_{zx}$，那么 Bob 手里的比特会坍缩到 $X^xZ^z \ket\psi$。只需要作用 $Z^zX^x$，即可还原出 $\ket\psi$。这个过程可以用如下电路来描述：

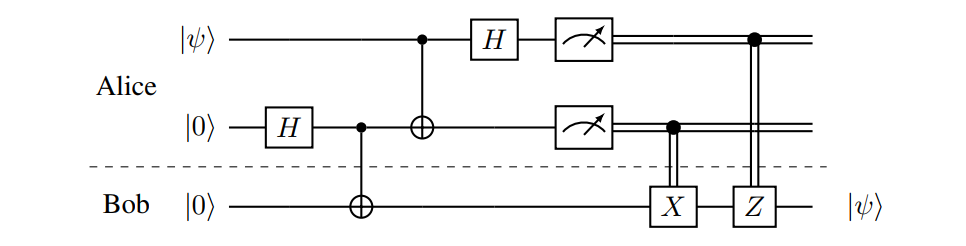
其中最开始的 $H, \mathrm{CNOT}$ 用于产生 Bell 基。

---

接下来的问题都是关于布尔函数 $f : {0, 1}^n\rightarrow {0, 1}$。此时我们将获得 $f$ 的一个 oracle 算符，它将对应的函数值装载到一个辅助比特上：
$$
U_f : \ket x\ket y \mapsto \ket x\ket{y\oplus f(x)}
$$
其中 $x$ 是 $n$-qubit 态，而 $y$ 是 $1$-qubit 态。那么容易发现有如下性质：

命题 1.2.1 (Phase Kickback) 一个 $f$ 的上述形式的 oracle 等价于将 $f(x)$ 装载到 $x$ 的相位上。
$$
U_f \ket x\ket - = (-1)^{f(x)}\ket x\ket -
$$

这个技巧可以用来解决下面的一系列问题。接下来我们将随机使用将函数值装载到辅助比特上的形式和装载到相位上的形式，应当可以通过上下文推断。

Deutsch 问题

给定一个 $f : {0, 1}\rightarrow {0, 1}$，判断 $f$ 是常函数还是 Balanced 函数。

Balanced 函数的定义是
$$
\mathrm{Pr}_x[f(x) = 1] = \frac 12
$$

注意到
$$
U_f\ket + = \frac{1}{\sqrt 2}((-1)^{f(0)}\ket 0 + (-1)^{f(1)}\ket 1)
$$
如果 $f(0)$ 和 $f(1)$ 是相同的，那么右边和 $\ket +$ 差一个全局相位，否则和 $\ket -$ 差一个全局相位。我们在标准正交基 ${\ket +, \ket -}$ 下测量此结果（即先作用 $H$ 再在 ${\ket 0, \ket 1}$ 下测量），即解决问题。因此电路为：

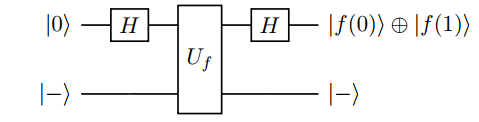
只查询了一次，经典必须查询两次，获得了常数级别的优化。

Deutsch-Jozsa 问题

给定一个 $f : {0, 1}^n\rightarrow{0, 1}$，保证 $f$ 或者是常函数，或者是 Balanced 函数。你需要区分这两种情况。

和上面的思路完全一样。首先制备一个均一叠加态（$H^{\otimes n}\ket 0^{\otimes n}$）
$$
\ket\psi = \frac 1{\sqrt{2^n}}\sum_{x\in{0, 1}^n} \ket x
$$
将此态通过 $U_f$ 得到
$$
U_f\ket\psi = \frac 1{\sqrt{2^n}}\sum_{x\in{0, 1}^n}(-1)^{f(x)} \ket x
$$
如果 $f(x)$ 是个常函数，那么此时得到的态和 $\ket\psi$ 只差一个全局相位。否则，$\ket\psi$ 在其中的投影长度为：
$$
\begin{aligned}
|\bra\psi U_f\ket\psi| &= \left|\frac 1\sum_{x\in{0, 1}^n} \bra x\sum_{y\in{0, 1}^n}(-1)^{f(y)} \ket y\right| \\
&=\left|\frac 1{2^n}\sum_{x\in{0, 1}^n}(-1)^{f(x)} \right| \\
&= 0
\end{aligned}
$$
也就是只需要在 $\ket \psi$ 扩充成的标准正交基下测量，如果测出 $\ket\psi$ 就回答常函数，否则回答 Balanced。当然实际上你没法“在 $\ket \psi$ 扩充成的标准正交基下测量”，合理的办法是先作用 $H^{\otimes n}$ 然后在 computational basis 下测量。最终电路为

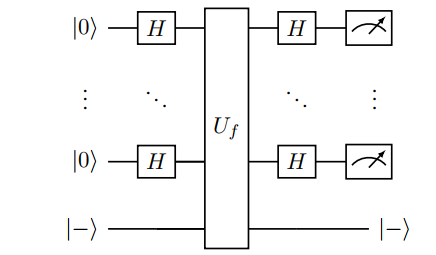
只查询了 $1$ 次。经典确定性算法复杂度为指数级，$1-\delta$ 概率成功的算法复杂度为 $O(\log 1/\delta)$。

Simon 问题

给定函数 $f: {0, 1}^n\rightarrow X$，其中 $|X|\geq 2^{n-1}$，你可以认为其中的值被离散化到了 ${0, 1}^m$，其中 $m \geq n-1$。保证 $f$ 满足性质：存在 $s$，$f(x) = f(y)$ 当且仅当 $x = y$ 或者 $x \oplus y = s$。你的任务是求出 $s$。

书上这个硬算感觉非常的不 intuitive。我们提供一个关于此问题的 insight：**$H^{\otimes n}$ 实际上是 Walsh-Hadamard 变换。**

考虑你对如下的态：
$$
\frac{1}{\sqrt{2^n}}\sum_{x\in{0, 1}^n}\ket x\ket{f(x)}
$$
作用上 $H^{\otimes n}\otimes I$，发生了什么。
$$
\begin{aligned}
&(H^{\otimes n}\otimes I)\frac{1}{\sqrt{2^n}}\sum_{x\in{0, 1}^n}\ket x\ket{f(x)} \\
=& \frac{1}{2^n}\sum_{x\in{0, 1}^n}\bigotimes_{i=1}^n(\ket 0 + (-1)^{x_i}\ket 1)\ket{f(x)} \\
=& \sum_{y\in {0, 1}^n}\ket y\color{red}\frac{1}{2^n}\sum_{x\in{0, 1}^n}(-1)^{x\cdot y}\ket{f(x)}
\end{aligned}
$$
红色的部分正是 $f(x)$ 在阿贝尔群 $G = \mathbb{Z}_2^n$ 下面的傅里叶变换（即 Walsh-Hadamard 变换）！

而这个问题中 $f$ 满足的性质是 $f(x) = f(x\oplus s)$。定义函数 $g_s(x) = [x = s]$，那么这个性质就是 $f = 2^n f * g$。两边做 Walsh-Hadamard 变换得到 $\hat f = 2^n \hat f \cdot \hat g$。而 $\hat g$ 实际上是
$$
\frac{1}{2^n}\sum_{y\in{0, 1}^n} (-1)^{x\cdot y}g(s) = \frac{(-1)^{s\cdot x}}{2^n}
$$
代入到关于 $\hat f$ 和 $\hat g$ 的关系式中，得到
$$
\hat f(x) = \hat f(x)\cdot (-1)^{x\cdot s}
$$
这表明如果 $x\cdot s\bmod 2 = 1$，那么 $\hat f(x) = 0$！而其他时候，简单验算一下发现 $\hat f(x)$ 的模长都是一样的。

回到原问题。先用 $U_f(H^{\otimes n}\otimes I)$ 制备带 $f$ 的均一叠加态，然后用 $H^{\otimes n}\otimes I$ 做 Walsh-Hadamard 变换，现在测量前 $n$ 个比特，将等概率得到 $x$，满足 $x\cdot s = 0$。重复 $k$ 次可以得到关于 $s$ 的 $k$ 个线性方程组。如果我们只随机 $n - 1$ 次，随出来的方程线性无关的概率是
$$
\prod_{i=1}^{n - 2}\left(1 - \frac 1{2^i}\right)\geq \prod_{i=1}^{\infty}\left(1 - \frac 1{2^i}\right)
$$
放缩这东西是一个经典高中题目，总之成功概率是常数。获得了这种线性无关的 $n - 1$ 个方程之后，立即可以解出 $s$。因此只需要 $O(n\log 1 / \delta)$ 次即可保证高概率成功。

经典算法只能进行生日悖论攻击，复杂度为 $O(2^{n / 2})$，我们实现了指数级加速。

基于量子傅里叶变换的算法

在上面的讨论中我们看到量子计算的能力很大一部分是来自它可以快速的做 Walsh-Hadamard 变换，即 $\mathbb{Z}_2^n$ 上的傅里叶变换。实际上，在接下来的讨论中我们将看到它可以做 $\mathbb{Z}_{2^n}$ 上的快速傅里叶变换：
$$
\ket x \mapsto \frac{1}{\sqrt{2^n}}\sum_{y\in[2^n]} e^{\frac{2\pi ixy}{2^n}} \ket y = \ket{\tilde{x}}
$$
根据经典结论，我们熟知傅里叶变换的逆是
$$
\ket {\tilde x} \mapsto \frac{1}{\sqrt{2^n}}\sum_{y\in[2^n]} e^{-\frac{2\pi i\tilde xy}{2^n}} \ket y = \ket x
$$

这里所有的 $\mathbb{Z}_{2^n}$ 中的整数都被编码成 $n$-qubit 量子态。我们考察这个变换实际上是在做什么：
$$
\begin{aligned}
\ket{x_1}\ket{x_2}\cdots\ket{x^n}\mapsto& \frac{1}{\sqrt {2^n}}\sum_{y\in[2]^n}\prod_{i=0}^{n-1}e^{\frac{2\pi i xy_i2^i}{2^n}}\bigotimes_{i=0}^{n-1}\ket{y_i} \\
=&\frac{1}{\sqrt {2^n}}\sum_{y\in[2]^n}\bigotimes_{i=0}^{n-1}e^{\frac{2\pi i xy_i2^i}{2^n}}\ket{y_i} \\
=& \bigotimes_{i=0}^{n - 1}\frac 1{\sqrt 2}(\ket 0 + e^{\frac{2\pi ix}{2^{n - i}}}\ket 1) \\
=& \bigotimes_{i=0}^{n - 1}\frac{1}{\sqrt 2}(\ket 0 + e^{2\pi i\cdot 0.x_ix_{i+1}…x_{n-1}}\ket 1)
\end{aligned}
$$
指数上的小数是二进制小数。剖析出傅里叶变换的本质是制作这样一个乘积态之后，我们自然得出如下暴力算法：

• 从 $0$ 到 $n - 1$ 枚举 $i$。

  • 让 $\ket{x_i}$ 变成 $\ket 0 + e^{2\pi i\cdot 0.x_i}\ket 1$。这其实就是在第 $i$ 个 qubit 上作用 Hadamard 门。

  • $j$ 从 $i + 1$ 到 $n - 1$ 递增。

    • 若 $x_j$ 是 $1$，那么将 $\ket 1$ 的相位乘上 $e^{\pi i / 2^{j - i}}$。这可以用受控 $R_k$ 门来实现，其中 $R_k$ 的 $SU(2)$ 表示是
      $$
      R_k = \begin{pmatrix}
      1 & 0 \\
      0 & e^{\frac{2\pi i}{2^k}}
      \end{pmatrix}
      $$

容易将上述过程实现成下面的电路（$\mathrm{QFT}$）：

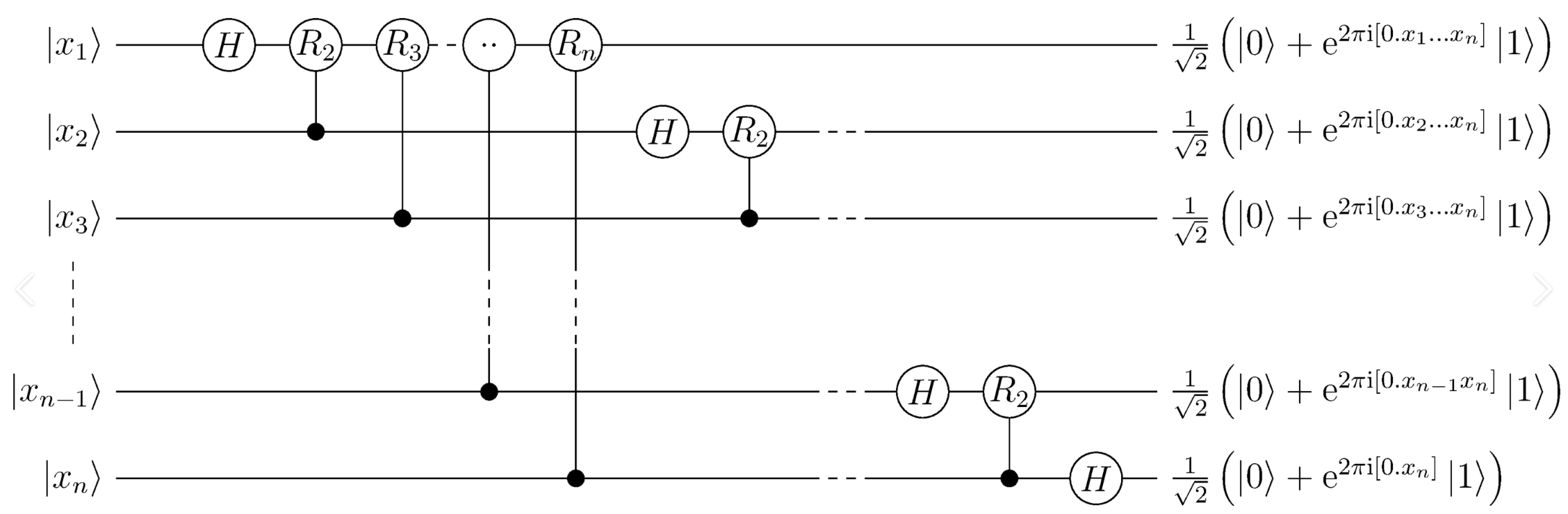
那么傅里叶变换的逆自然就是（$\mathrm{QFT}^{\dagger}$）

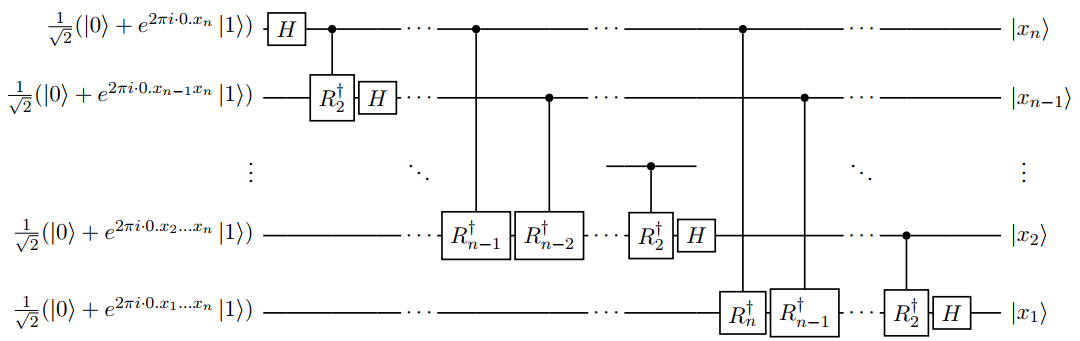
量子相位估计

给定一个酉算符 $U$ 的受控门，和 $U$ 的一个本征态 $\ket \psi$，满足 $U\ket \psi = e^{i\theta} \ket \psi$。

目标是求 $\theta$。

首先考虑 $\theta = 2\pi\cdot 0.x_0x_1…x_{n - 1}$。观察上文，我们已经实现了 IQFT，这个算法可以将装载在相位上的二进制小数恢复出来。那么我们的想法很简单，就是制备所有的
$$
\ket 0 + e^{2\pi i\cdot 0.x_{i}…x_{n - 1}}\ket 1
$$
注意到
$$
\begin{aligned}
&(\op 0 \otimes I + \op 1\otimes U^{2^k})(H\otimes I)\ket 0\ket \psi \\
=& (\op 0 \otimes I + \op 1\otimes U^{2^k})\frac 1{\sqrt 2}(\ket 0 + \ket 1)\ket\psi \\
=& \frac 1{\sqrt 2}\ket 0\ket \psi + \frac{1}{\sqrt 2}\ket 1
U^{2^k}\ket \psi \\
=& \frac{1}{\sqrt 2}(\ket 0 + e^{2\pi i\cdot 0.x_k…x_{n - 1}}\ket 1)\ket \psi
\end{aligned}
$$
实现成电路就是

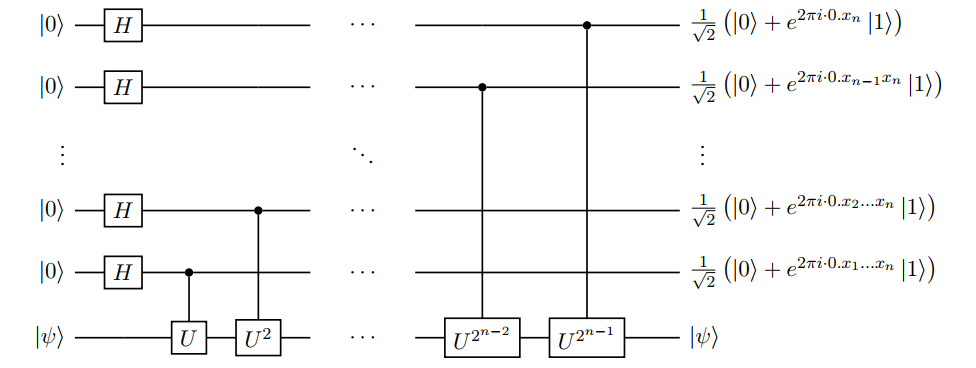
总共使用的门数量为 $O(2^n + n)$。

那么只需要在前 $n$ 个 qubit 上接上 $\textrm{QFT}^{\dagger}$，即可恢复出 $x_0, …, x_{n - 1}$。

在 $\theta / 2\pi$ 的二进制小数表示超过 $n$ 位时，直觉上误差也不会很大。这里我们具体计算一下测量出结果的分布。

假设 $U\ket\psi = e^{2\pi i \varphi}\ket\psi$，那么经过 Hadamard 门和受控 $U$ 门阵列之后得到的态是
$$
\bigotimes_{i=1}^n\frac{1}{\sqrt 2}(\ket 0 + e^{\pi i2^{i}\varphi}\ket 1) = \frac{1}{\sqrt{2^n}}\sum_{x = 0}^{2^{n} - 1}e^{i\varphi x}\ket x
$$
再做 $\mathrm{QFT}^{\dagger}$ 得到（注意此时 $\varphi - 2\pi y / 2^n$ 非零，后面是一个等比数列，方便起见记 $\tilde \varphi = \varphi - 2\pi y / 2^n$）
$$
\begin{aligned}
\frac{1}{2^n}\sum_{x = 0}^{2^n - 1}\sum_{y = 0}^{2^n - 1}e^{i\varphi x}e^{-\frac{2\pi i xy}{2^n}}\ket y &= \frac{1}{2^n}\sum_{x = 0}^{2^n - 1}\ket y\sum_{x = 0}^{2^n - 1}\exp\left(ix\left(\varphi - \frac{2\pi y}{2^n}\right)\right) \\
&= \frac{1}{2^n}\sum_{y = 0}^{2^n - 1}\ket y\frac{1 - e^{i\tilde\varphi2^{n}}}{1 - e^{i\tilde\varphi}}
\end{aligned}
$$
测出结果为 $y$ 的概率为
$$
\begin{aligned}
\mathrm{Pr}[y] =& \frac{1}{2^{2n}}\left|\frac{1 - e^{i\tilde\varphi2^n}}{1 - e^{i\tilde\varphi}}\right|^2 \\
=&\frac{1}{2^{2n}}\left|\frac{1 - \cos\tilde\varphi2^n - i\sin\tilde\varphi2^n}{1 - \cos\tilde\varphi - i\sin\tilde\varphi}\right|^2 \\
=&\frac{1}{2^{2n}}\left|\frac{2\sin^2\frac{\tilde\varphi2^n}{2} + i\cdot 2\sin\frac{\tilde\varphi2^n}{2}\cos\frac{\tilde \varphi2^n}{2}}{2\sin^2\frac{\tilde\varphi}{2} + i\cdot 2\sin\frac{\tilde\varphi}{2}\cos\frac{\tilde \varphi}{2}}\right|^2 \\
=&\frac{1}{2^{2n}}\frac{\sin^2\left(\left(\varphi - \frac{2\pi}{2^n}y\right)2^{n - 1}\right)}{\sin^2\left(\left(\varphi - \frac{2\pi}{2^n}y\right) / 2\right)}\color{lightgrey}\left|\frac{\exp(i\tilde\varphi 2^{n - 1})}{\exp(i\tilde\varphi / 2)}\right|^2
\end{aligned}
$$

命题 2.1.1. 设 $\frac{2\pi k}{2^n}\leq \varphi \leq \frac{2\pi(k + 1)}{2^n}$，则测出 $y = k$ 和 $y = k + 1$ 的概率和至少是 $\frac{8}{\pi^2}$。

证明. 纯 Dirty work，求导发现 $\varphi$ 在中间的时候答案最小，然后直接带进去硬放。

总结起来，我们得到如下结论：

定理 2.1.2. 给定酉算符 $U$ 和本征向量 $\ket\varphi$，可以用 $O((\log 1 / \varepsilon)^2)$ 的 $\mathrm{QFT}^{\dagger}$和 $O(1/\varepsilon)$ 的受控 $U$ 门，来以至少 $\frac{8}{\pi^2}$ 获得其特征值的相位的一个绝对误差至多为 $\varepsilon$ 的近似。

求元素的阶

给定正整数 $a$ 和 $N$，求最小的正整数 $r$ 使得 $a^r\equiv 1\pmod n$。

保证 $\gcd(a, N) = 1$。

由于 $\gcd(a, N) = 1$，$U : \ket x \mapsto \ket{ax}$ 是酉变换。此变换有高效的经典算法实现，所以 $U$ 是可以制作的。

记 $\langle a\rangle$ 是 $a$ 在 $\bmod n$ 乘法群中生成的子群。考虑 $\langle a\rangle$ 作用在 $\mathbb{Z}_N^* = {1, …, N - 1}$ 上，作用为乘法。根据轨道 - 稳定子定理，每个轨道的大小都相同。方便起见，我们取 $1$ 所在的轨道 $1^{\langle a\rangle}$ 来研究，这个轨道是 $G$ 的不变子空间（实际上在后面的算法中，你会发现我们的态矢确实都落在这个不变子空间中）。这个子空间同构于 $\mathbb{Z}_{r}$ 上的加法群。在加法群上，我们的酉变换 $U$ 实际上相当于 $P : \ket x \mapsto \ket{x + 1\bmod r}$。这是一个循环矩阵，我们熟知它的特征值是 $e^{-2\pi ik / r}$，对应特征向量
$$
\ket{\tilde k} = \frac{1}{\sqrt r}\sum_{x = 0}^{r - 1}e^{\frac{2\pi ikx}{r}}\ket x
$$
那么回到乘法群上，$G | 1^{\langle a\rangle}$ 的特征向量是
$$
\ket{u_k} = \frac{1}{\sqrt r}\sum_{x = 0}^{r - 1}e^{\frac{2\pi i kx}{r}}\ket{a^x\bmod N}
$$
自然，它也是 $G$ 的一个特征向量。如果我们对 $u^k$ 做相位估计，立即得到 $1 - k / r$ 的估计。只需要解决下面的问题：

• 如何在不知道 $k, r$ 的情况下制备 $\ket {u_k}$？
• 如何用估计值逼近 $k / r$ 的真实值？
• 如果 $k, r$ 有公因子，如何区分是否约分？

如何在不知道 $k, r$ 的情况下制备 $\ket {u_k}$？

我们虽然不能制备 $\ket{u_k}$，但是可以制备 $\ket{u_k}$ 关于 $k$ 的均一叠加。
$$
\frac{1}{\sqrt r}\sum_{k = 0}^{r - 1}\ket{u_k} = \frac{1}{r}\sum_{k = 0}^{r - 1}\sum_{x = 0}^{r - 1}e^{\frac{2\pi i k x}{r}}\ket{a^x\bmod N} = \ket{1\bmod N}
$$
这样一来我们做 Phase Estimation 后测量，就能够知道估计值 $\widetilde{k / r}$，其中 $k$ 从 $[r]$ 中均一抽取。注意这时候制备 $U^{2^k}$ 的时候，只需要 ${\rm poly}(k)$ 个门（使用快速幂）。因此此时相位估计的开销为 $O({\rm poly}(m))$。其中 $m$ 是选定的有效位数。

如何用估计值逼近 $k / r$ 的真实值？

这里我们选择使用连分数逼近来得到 $k / r$ 的真实值。我们 input 连分数逼近的如下性质：

定理 2.2.1. 对于任意的实数 $x$，$p/q$ 是 $x$ 的渐进分数当且仅当它是 $x$ 的第二类最优逼近。即对于任意的 $0 < b\leq q$，$a, b\in \mathbb{Z}$，且 $a/b\ne p/q$ 都有
$$
|bx - a| > |qx - p|
$$

我们取 $n$ 使得 $2^n > 2r^2$（此时 $n$ 为 $\log N$ 级别），然后做 $n$ 位的相位估计。此时将得到 $k / r$ 的估计 $x$，满足

$$
\left|x - \frac kr\right| < \frac{1}{2^n} \quad \Rightarrow \quad \left|x - \frac kr\right| < \frac{1}{2r^2}
$$

不妨设 $x = k/r + \Delta$，其中 $\Delta < 1 / 2r^2$。现在证明 $k / r$ 是 $x$ 的第二类最优逼近。考虑 $a, b$，有

$$
\begin{aligned}
\left|x - \frac ab\right| =& \left|\frac{k}{r} - \frac{a}{b} + \Delta\right| \\
\geq& \frac 1{br} - |\Delta| \\
\ge & \frac{1}{2r^2}\frac{r}{b} \\
\ge & \frac rb\left|x - \frac kr\right|
\end{aligned}
$$

化简即得到 $|bx - a| > |rx - k|$。因此 $k / r$ 必将出现在 $x$ 的连分数逼近序列中。此序列的长度为 $O(n)$ 级别，因为求连分数逼近的过程就是在对分子分母做辗转相除。

因此只需要对 $x$ 的连分数逼近的每一项 $p / q$ 验证 $q$ 是否是 $a$ 的阶即可。如果碰巧你抽到的 $k$ 和 $r$ 互质，你就能找到这个阶。

如何处理 $k$ 和 $r$ 不互质的情况？

因为 $k$ 是从 $[r]$ 中均一抽取的，所以我们抽到一个互质的 $k$ 的概率是 $\varphi(k) / k$。其中 $\varphi$ 是欧拉函数。

著名的结果是 $\varphi(n) / n = \Omega(1 / \log\log n)$，因此随 $\log\log N$ 次就可以高概率成功。

Shor 算法

首先可以排除两种平凡的情况：

• $n$ 是偶数，直接返回 $2$
• $n = p^{\alpha}$。计算 $n$ 的 $2, 3, …, \log_3$ 次方根，判断是不是整数。
• $n$ 是素数，可以用 AKS 素性测试。

算法的核心思路是找到 $1$ 的二次剩余。设 $x\ne \pm 1$ 且 $x^2 \equiv 1\pmod N$，那么
$$
kN = (x + 1)(x - 1)
$$
$(x + 1)$ 和 $(x - 1)$ 不可能都和 $N$ 互质。

然后我们在 ${1, …, N - 1}$ 里面随机一个 $x$，如果 $\gcd(x, N)$ 不是 $1$，直接返回此数。否则用上一节的算法求 $x$ 的阶 $r$。如果 $r$ 是偶数且 $x^{r / 2}$ 不是 $-1$（条件 $\star$），我们的算法就结束，否则重复。

---

首先设 $N = \prod_{i = 1}^l p_i^{\alpha_i}$用中国剩余定理把 $x$ 打到模 $p_i^{\alpha_i}$ 的环上去。在 $N$ 中随机 $x$ 等价于随机
$$
(x_1, …, x_l)\in \prod_{i=1}^l \mathbb{Z}_{p_i^{\alpha_i}}^*
$$
只要任意一个 $x_i$ 在 $\mathbb{Z}_{p_i}^{\alpha_i}$ 中满足 $(\star)$，$x$ 就满足 $(\star)$。

首先熟知奇素数的幂都有原根 $g$，因此存在同构 $\tau : \mathbb{Z}_{p^{\alpha}}^*\cong \mathbb{Z}_{\varphi(p^{\alpha})}$。设 $n = \varphi(p^\alpha)$。设我们随机到的 $x = g^s, -1 = g^{t}$，设 $n = 2^k q$，其中 $q$ 是奇数，那么：

• $x$ 的阶是 $n / \gcd(n, s)$。
• $x^{r / 2} = -1$ 等价于 $sr = 2t$。
• 因为 $-1$ 是二阶元，所以 $\gcd(n, t) = 2$。

现在考虑如下情况：$s$ 是奇数。显然，这种情况出现的概率为 $1/2$。而出现这种情况时：

-

基于 $SU(2)$ 旋转的量子算法

Grover

我们期望解决下面所述的无结构搜索问题：

问题. 给定一个函数 $f : [n] \rightarrow \\{0, 1\\}$，包装成一个 oracle：

$$
|x, z\rangle \xmapsto{U_f} |x, z \oplus f(z)\rangle
$$

搜索其中的一个 $x$，满足 $f(x) = 1$。

首先考虑使用 phase kickback 技巧：

$$
|x, -\rangle \xmapsto{U_f \otimes I} (-1)^{f(x)}|x, -\rangle
$$

这个操作（带有一个辅助比特）成为一次 phase query。考虑这个操作作用在一个均一叠加态 $|\psi\rangle = 1 / \sqrt{n} \sum_{x = 1}^n |x\rangle$ 上：

$$
|\psi\rangle\xmapsto{\text{phase query}} \left(\sum_{x:f(x) = 0}|x\rangle\right) - \left(\sum_{x:f(x) = 1}|x\rangle\right)
$$

这个操作形如某种“反射”。Grover 算法的出发点是，用两种“反射”构造“旋转”，将均一叠加态转到 $f(x) = 1$ 的方向。

---

首先考虑只有一个元素 $w$ 使得 $f(w) = 1$ 的情况。那么上述的 phase query 写成酉矩阵就是

$$
U = I - 2|w\rangle\langle w|
$$

接下来定义（$\psi$ 是均一叠加态）

$$
V = 2|\psi\rangle\langle\psi| - I
$$

我们来制备此门。注意为了实现类似于分支判断的操作，受控门是一个很好的选择，但是受控门对叠加态并不友好。所幸我们注意到

$$
V = H^{\otimes m}(2|0^m\rangle\langle0^m| - I)H^{\otimes m}
$$

因此下图用 $O(\log n)$ 个门制备了该门。

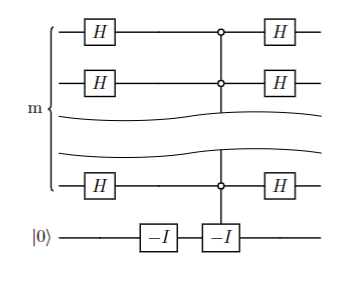
万事俱备。Grover 算法的完整过程如下：

• 制备均一叠加态 $|\psi\rangle$（$O(\log n)$ 个门）
• 重复 $t = \pi / 4\sqrt{n}$ 次
  • 作用 $U$。
  • 作用 $V$。
• 测量。

做一些简单的计算：

$$
\begin{align}
U|\psi\rangle &= |\psi\rangle - \frac{2}{\sqrt n}|w\rangle \\
U|w\rangle &= -|w\rangle \\
V|\psi\rangle &= |\psi\rangle \\
V|w\rangle &= \frac{2}{\sqrt n} |\psi\rangle - |w\rangle
\end{align}
$$

因此 $|\psi\rangle, |w\rangle$ 生成 $U, V$ 下的不变子空间。方便起见，我们将这组基 Schmidt 正交化为 $|w\rangle, |w^\perp\rangle$，其中

$$
|w^\perp\rangle = \frac{|\psi\rangle - \langle w|\psi\rangle|w\rangle}{\parallel |\psi\rangle - \langle w|\psi\rangle|w\rangle\parallel}
$$

于是（假设 $\theta = \arcsin \frac{1}{\sqrt n}$）

$$
\begin{align}
|\psi\rangle &= \frac{1}{\sqrt n}|w\rangle + \sqrt{1 - \dfrac{1}{n}}|w^\perp\rangle \\
&= \sin\theta |w\rangle + \cos\theta|w^\perp\rangle
\end{align}
$$

现在可以方便地在 $|w\rangle, |w^\perp\rangle$ 下研究 $U, V$ 的矩阵表示，我们将看到它正是平面内旋转 $2\theta$ 度：

$$
U = \begin{pmatrix}
-1 & 0 \\
0 & 1
\end{pmatrix}, V = \begin{pmatrix}
-\cos 2\theta & \sin 2\theta \\
\sin 2\theta & \cos 2\theta
\end{pmatrix},
VU = \begin{pmatrix}
\cos 2\theta & \sin 2\theta \\
-\sin 2\theta & \cos 2\theta
\end{pmatrix}
$$

因此

$$
(VU)^t|\psi\rangle = \sin (2t + 1)\theta|w\rangle + \cos(2t + 1)\theta|w^\perp\rangle
$$

如果在标准正交基下测量，想要使得 $w$ 的出现概率尽可能大，就要使得 $(2t + 1)\theta \rightarrow \frac{\pi}{2}$，即 $t\simeq \frac{\pi}{4}\sqrt n$。

Quantum Random Walk

Quantum Random Walk 中的旋转变换

考虑一个有稳态 $\pi$、且在 $\pi$ 上细致平衡随机游走 $P$。细致平衡定义为：
$$
\pi_iP_{ij} = \pi_j P_{ji}
$$
定义其 Discriminant Matrix 为
$$
D_{ij} = \sqrt{P_{ij}P_{ji}}
$$

容易证明此矩阵满足如下性质：

命题 4.2.1. $P$ 的稳态 $\ket\pi = \sum_i\sqrt{\pi_i}\ket i$ 是 $D$ 的本征值为 $1$ 的特征向量，且因为 $D$ 和 $P$ 是相似的：
$$
D = \mathrm{diag}(\sqrt \pi) P (\mathrm{diag}(\sqrt \pi))^{-1}
$$
所以他们有相同的本征值。

证明. 对于第一个断言
$$
\begin{aligned}
\bra i D\ket \pi &= \sum_{j} D_{ij}\braket{j}{\pi} \\
&= \sum_{j}\sqrt{P_{ij}P_{ji}}\sqrt{\pi_{j}} \\
&= \sum_{j}\sqrt{\pi_i}P_{ij} = \sqrt{\pi_i}
\end{aligned}
$$
且 $D_{ij} = \sqrt{P_{ij}P_{ji}} = \sqrt{\pi_i}P_{ij}(\sqrt{\pi_j})^{-1} = (\mathrm{diag}(\sqrt \pi) P (\mathrm{diag}(\sqrt \pi))^{-1})_{ij}$。

假设给定了如下的 Oracle
$$
O_p \ket{0^n}\ket j = \sum_k \sqrt{P_{jk}}\ket k\ket j
$$
可以通过如下方法把 $D$ 编码在电路中：令
$$
U_D = O_p^\dagger \cdot \mathrm{SWAP} \cdot O_p
$$
这是一个 Hermit 算子。则有

命题 4.2.2. 对于任意的 $i, j\in[N]$ 都有
$$
\bra i \bra{0^n} U_D\ket{0^n}\ket j = D_{ij}
$$
即
$$
U_D = \begin{pmatrix} D & \cdot \\
\cdot & \cdot \end{pmatrix} = \ket{0^n}\bra{0^n}\otimes D + \cdots
$$
此形式称作 $D$ 的块编码。

证明. 直接硬算：
$$
O_p \ket{0^n}\ket j = \sum_k \sqrt{P_{jk}}\ket k\ket j
$$
因此
$$
\begin{aligned}
\bra i\bra{0^n}U_D\ket {0^n}\ket j &= (O_p\ket i\ket{0^n})^\dagger (\mathrm{SWAP\cdot}O_p\ket{0^n}\ket j) \\
&= \sum_{k}\sqrt{P_{ik}}\bra k\bra i\sum_{k’}\sqrt{P_{jk’}}\bra j\bra {k’} \\
&= \sqrt{P_{ji}P_{ij}} = D_{ij}
\end{aligned}
$$

假设 $D$ 有谱分解 $D = \sum_i \lambda_i\op{v_i}$，那么 $U_D$ 作用在一个特征向量上就是
$$
U_D\ket{0^n}\ket{v_i} = \ket{0^n}D\ket{v_i} + \ket{\tilde\bot_i} = \lambda_i \ket{0^n}\ket{v_i} + \ket{\tilde\bot_i}
$$
其中 $\ket{\tilde\bot_i}$ 已经和前面的态正交。需要注意到的是 $\ket{0^n}\ket{v_i}$ 和 $\ket{\tilde\bot_i} = \sqrt{1 - \lambda_i^2}\ket{\bot_i}$ 张成了 $U_D$ 的不变子空间：在上式两边同时作用 $U_D$ 得到
$$
\ket{0^n}\ket{v_i} = \lambda_i(\lambda_i\ket{0^n}\ket{v_i} + \sqrt{1 - \lambda_i^2}\ket{\bot_i}) + \sqrt{1 - \lambda_i^2}U_D\ket{\bot_i} \\
\Rightarrow U_D\ket{\bot_i} = \sqrt{1 - \lambda_i^2}\ket{0^n}\ket{v_i} - \lambda_i\ket{\bot_i}
$$
那么 $U_D$ 在基 $\beta_i = { \ket{0^n}\ket{v_i}, \ket{\bot_i}}$ 下的矩阵表示就是
$$
[U_D]_{\beta_i} = \begin{pmatrix}
\lambda_i & \sqrt{1 - \lambda_i^2} \\
\sqrt{1 - \lambda_i^2} & -\lambda_i
\end{pmatrix}
$$
如果我们能做关于第一个基向量的反射：
$$
Z_\Pi = I - 2\op{0^n}
$$
那么就可以获得一个旋转矩阵 $O_D = U_DZ_{\Pi}$，其 $SU(2)$ 表示为
$$
[O_D]_{\beta_i} = \begin{pmatrix}
\lambda_i & \sqrt{1 - \lambda_i^2} \\
-\sqrt{1 - \lambda_i^2} & \lambda_i
\end{pmatrix} = \begin{pmatrix}
\cos\theta_i & \sin\theta_i \\
-\sin\theta_i & \cos\theta_i
\end{pmatrix}
$$
实际上 $Z_\Pi$ 的制作可以使用 $n$ 路 Toffoli 门，因此如下电路可以实现 $O_D$：

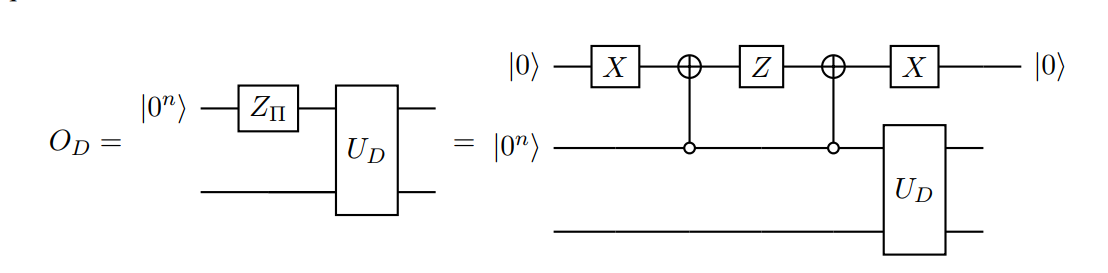
命题 4.2.3. $O_D$ 的特征值为 $e^{\pm i\arccos(\lambda_i)}$。

证明. 直接特征方程，其根为
$$
x = \frac{2\cos\theta_i \pm \sqrt{4\cos^2\theta_2 - 4}}{2} = e^{\pm i\theta_i}
$$

因为 $\arccos(1 - \delta) = O(\sqrt{2\delta})$，所以 $O_D$ 的 spectral gap 是 $D$ 的根号倍，实现了 spectral gap amplification。

判断完全图中是否有标记

考虑如下抽象的简单问题：

隐藏一个完全图，只可能有两种情况：

• 图中所有点都不带标记。
• 图中有 $m$ 个点带标记。（$m = o(1)$）

每次你可以询问一个点 $u$，oracle 以等概率返回其邻居和其自身，如果询问的点有标记，则总是返回自己。

你需要区分这两种情况。

在经典情况下，你只能尝试硬问，打中带标记的点的期望时间为 $n/m$。而在量子情况下，假设上述询问被打包成了一个 oracle $U_D$，那么我们可以制备 $O_D$。

在情况 1 下，矩阵 $P$ 为 $\frac 1N e_Ne_N^{T}$，只有 $e_N$ 是其特征值为 $1$ 的特征向量，其余特征向量的特征值都是 $0$。

在情况 2 下，矩阵 $\tilde P$ 为
$$
\tilde P = \begin{pmatrix}
I & 0 \\
\frac{1}{n}J_{n - m, m} & \frac 1n J_{n - m, n - m}
\end{pmatrix}
$$
其中 $J_{XY} = e_X^Te_Y$。那么其 discriminant matrix 就是
$$
\tilde D = \begin{pmatrix}
I & 0 \\
0 & \frac{1}{n}J_{n - m, n - m}
\end{pmatrix}
$$
容易看到该矩阵的特征值为 $1$（重数为 $m$），$(n - m) / n$（重数为 $1$），一堆 $0$。

注意到：令初状态为
$$
\ket{0^n}\ket\psi = \ket{0^n}\frac 1{\sqrt{n}}\sum_{i=1}^n\ket i
$$
那么 $\ket \psi$ 是 $D$ 的特征值为 $1$ 的特征向量，在 $\beta_1$ 中的旋转为 $0$ 度旋转，无论如何最后测量第一个寄存器都将得到 $1$。

而
$$
\ket\psi = \sqrt{\frac{m}{n}}\ket{\tilde\pi} + \sqrt{\frac{n - m}{n}}\ket{\tilde{v}}
$$
其中 $\ket{\tilde\pi} = \sum_{i=1}^m \frac{1}{\sqrt m}\ket i$，是特征值为 $1$ 的特征向量，$\ket{\tilde v} = \sum_{i=m + 1}^{n}\frac{1}{\sqrt{n - m}}\ket 1$ 是特征值为 $\frac{n - m}{n}$ 的特征向量。记 $\varepsilon = m / n$（这个值实际上是 $\tilde D$ 的 spectral gap）。我们作用 $k = \pi / (2\arccos\frac{n - m}{n}) = O(\sqrt{m / n})$ 次 $O_{\tilde D}$，即可得到
$$
O_{\tilde D}^k = \sqrt{\varepsilon}\ket{0^n}\ket\pi + \ket{\tilde \bot_k}
$$
测出 $0$ 的概率只有 $\varepsilon$。于是用 $O(1 / \sqrt{\varepsilon})$ 次量子游走然后测量 $0$ 来高概率成功区分此问题。

元素区分问题

首先我们列举一个证明超出能力范围的事实（上面的讨论中虽然把这个问题的复杂度分析清楚了，但是非常 adhoc）

给定一个在强正则图 $G$ 上的，启动时间为 $S$，转移时间为 $U$，检验是否为标记元素时间为 $C$ 的随机游走，若被标记元素的比例至少为 $\varepsilon$，$G$ 的 spectral gap 为 $\delta$，则量子游走可以在如下时间内解决问题：
$$
S + \frac{1}{\sqrt{\delta\varepsilon}}(U + C)
$$

元素区分问题是这样的一个问题：

给定一个一个函数 $f : {1, 2, …, N}\rightarrow S$，判断是否存在 $x, y$ 使得 $f(x) = f(y)$。

有一个与其非常类似的问题，称作 collision problem，其形式如下：

给定一个函数 $f$，它或者是一对一的，或者是严格二对一的，区分这两种情况。

解法. 首先取前 $B$ 个元素，用经典算法断定这些元素是否两两不同。如果没找到，用 Grover 算法在后面的元素中找和前面一样的元素（假设你可以把前 $B$ 个元素存下来，然后 $O(1)$ 判断是不是相同）。因为好元素的个数是 $B$ 个，所以 Grover 的复杂度是 $O(\sqrt{n / B})$。取 $B = n^{1/3}$ 得到复杂度 $O(n^{1/3})$。

复杂度下界. 可以证明此问题复杂度下界就是 $O(n^{1/3})$。

我们用 collision problem 的下界证明元素区分问题的下界。假设能在 $T(n)$ 时间内解决规模为 $n$ 的元素区分问题。那么对于 collision problem，我们随机取 $\sqrt n$ 个元素（这里正确的做法是取 $[\sqrt n]\rightarrow [n]$ 的哈希函数）做生日悖论攻击，如果元素区分问题给出了重复元素，那么函数就是二对一的，从而在 $T({\sqrt n})$ 时间内解决了 collision problem，因此
$$
T(\sqrt n)\geq n^{1/3}
$$
得到 $T(n) = \Omega(n^{2/3})$。而这个下界确实可以用量子游走达到。这个算法的设计遵循 Hamming 图上的量子游走范式。

定义 4.2.4. Hamming 图 $H(n, m)$ 是这样的一个图：

• 图的点集是 $[n]^m$。
• 两个点连边当且仅当其 hamming distance 为 $1$。

标记一个点当且仅当一个点表示的向量中存在 $x\ne y, f(x) = f(y)$。则标记的点占比至少为
$$
\varepsilon\geq \frac{1}{N^M}\binom M 2 \cdot 2 \cdot (N - 2)^{M - 2} = \frac{M(M - 1)\cdot (N - 2)^{M -2}}{N^M}
$$
接下来需要知道 Hamming 图的谱信息。Hamming 图的邻接矩阵是
$$
\begin{aligned}
A &= (J - I)\otimes I \otimes \cdots \otimes I \\
&+ I \otimes (J - I)\otimes \cdots \otimes I \\
&\ \ \vdots \\
&+I\otimes I\otimes \cdots \otimes (J - I)
\end{aligned}
$$
我们来计算 $A$ 的特征值。首先从 $(J - I)$ 入手，他有重数为 $1$ 的特征值 $(n - 1)$ 和重数为 $n - 1$ 的特征值 $-1$。对应的特征向量全都是 $I$ 的特征向量。因此 $A$ 的 $n^m$ 个特征向量形如：
$$
\ket {v_1}\ket{v_2}\cdots\ket{v_m}
$$
其中 $\ket{v_i}$ 为 $(J - I)$ 的特征值。其特征值形如 $(n - 1)\cdot k + (-1)\cdot(m - k)$。所以最大特征值是 $N(M - 1)$，其次是 $N(M - 1) - M$。对应的随机游走的 spectral gap 是
$$
\delta = \frac{N}{M(N - 1)}
$$
观察上面的复杂度式子，你肯定不会希望每次量子游走完之后为了计算是不是标记状态，还要给每一维查一次 $f$。所以正确的做法是把所有的 $f$ 带着一起走，维护
$$
\ket{x_1, x_2, …, x_m, f(x_1), f(x_2), …, f(x_m), \text{DS}}
$$
其中 $\textrm{DS}$ 是一些 $O(m)$ 空间经典数据结构，比如哈希表，然后你就可以实现：

• $S = m$，一开始需要查 $m$ 次 $f$。

• $U = O(1)$，每次修改需要查两次 $f$：
  $$
  \begin{aligned}
  &\ket{x_1, x_2, …, x_m, f(x_1), f(x_2), …, f(x_m), \text{DS}} \\
  \xrightarrow{U_f^{\dagger}} & \ket{x_1, x_2, …, x_m, 0, f(x_2), …, f(x_m), \text{DS}} \\
  \rightarrow& \ket{x_1’, x_2, …, x_m, 0, f(x_2), …, f(x_m), \text{DS}}\\
  \xrightarrow{U_f} & \ket{x_1’, x_2, …, x_m, f(x_1’), f(x_2), …, f(x_m), \text{DS}} \\
  \end{aligned}
  $$

• $C = O(1)$，因为所有东西都存好了。

根据上面的理论，最终复杂度是
$$
M + \sqrt{\frac{M(N - 1)N^M}{N\cdot M(M - 1)\cdot (N - 2)^{M -2}}} = O\left(M + \frac{N}{\sqrt M}\right)
$$
取 $M = N^{2/3}$ 得到最优复杂度。

我总感觉这里差了很多东西，而且那个硬套的 $\textrm{DS}$ 也非常难绷。但是只能不管了。

基于 Hamiltonian 模拟的算法

称一个 $n$-qubit 的哈密顿量 $H$ 能够被高效模拟，若对于任意的 $t > 0, \varepsilon > 0$，存在一个电路包含 ${\rm poly}(n, t, 1/\varepsilon)$ 个门的电路 $U$ 使得 $\Norm{U - e^{-iHt}} \leq \varepsilon$。我们一般假设 $\Norm H = \mathrm{poly}(n)$。这里 $\Norm \cdot$ 是谱范数，即最大奇异值。

注意下文中高效模拟和高效实现是两回事。高效实现就是实现 $U$，要求 $U$ 是 unitary，高效模拟是实现 $e^{-iHt}$，要求 $H$ 是 Hermitian。

有一些简单的结论

1. 若 $H$ 只作用在常数个 qubit 上，那么 $H$ 可被高效模拟。

   考虑 Solovay-Kitaev 定理。

2. 若 $H$ 能被高校模拟，那么 $cH$ 能被高效模拟。（$c = \mathrm{poly}(n)$）

   注意 $H = cHc^{-1}$，因此要拟合 $e^{-icHt}$，只需要将 $t$ 乘 $c$ 即可。对于 $c < 0$ 的情况，只需要先造 $c > 0$ 的，然后对电路取 $\dagger$。

3. 若 $H$ 能被高效模拟，$U\in \mathbb{C}^{2^n\otimes 2^n}$ 能被高效实现，那么 $UHU^\dagger$ 能被高效模拟。

   只需注意到 $e^{i(uHU^\dagger)t} = Ue^{-iHt}U^\dagger$。

4. 若 $H\in \mathbb{C}^{2^n\times 2^n}$ 是对角的，且对角元 $\bra k H\ket k$ 都能被高效计算，那么 $H$ 能被高效模拟。

   若 $H$ 是对角的，那么只需要实现 $\ket{d(k)}\mapsto e^{-id(k)t}$。为了保证常数误差，只需要将 $d(k)$ 算成精度为 $l = \log_21/\varepsilon$ 的浮点数。假设 $d(k) = 0.d_1…d_l$，存在 $l$ 个 qubit 当中，那么只需要如下的门：
   $$
   R_Z(-t / 2^j) = \begin{pmatrix}
   1 & 0 \\
   0 & e^{-it / 2^j}
   \end{pmatrix}
   $$
   作用 $l$ 次，即可实现目标。

乘积公式

称 $H$ 是 $k$-local 哈密顿量，若它是若干个作用在至多 $k$ 个 qubit 上的 Hamiltonian 的和。

接下来考虑如下问题：

若 $H_1, H_2$ 能被高效模拟，那么 $H_1 + H_2$ 是否能被高效模拟？

若 $H_1, H_2$ 对易，那么是显然的。但大多数情况下 $H_1, H_2$ 并非对易，此时我们有

定理 5.1.1 (Lie product formula)
$$
e^{-i(H_1 + H_2)t} = \lim_{m\rightarrow \infty}\left(e^{-iH_1t / m}e^{-iH_2t/m}\right)^m
$$
证明. 定量分析收敛速度。即我们想要知道 $m$ 为多大时
$$
\Norm{\left(e^{-iH_1t / m}e^{-iH_2t/m}\right)^m - \left(e^{-i(H_1 + H_2)t / m}\right)^m} \leq \varepsilon \tag{$\triangle$} \label{ieq:e-e}
$$
注意
$$
\begin{aligned}
\Norm{a^m - b^m} &= \Norm{(a - b)\left(\sum_{i=0}^{m - 1}a^i b^{m - 1 - i}\right)} \\
&\leq m\left\lVert a - b \right\rVert (\max{\norm a, \norm b})^m
\end{aligned}
$$
上式中的 $e^{(\cdot)}$ 都是酉矩阵，因此后面的 $\max$ 项是 $0$。要计算 $\left\lvert a - b \right\rvert$，我们将 $e^{(\cdot)}$ 泰勒展开，经过一些平凡的计算得到 $\ref{ieq:e-e}$ 左侧为
$$
O\left(\frac 1m \max{\Norm {-iH_1 t}, \Norm{-iH_2 t}}^2\right) \leq \varepsilon
$$
得到
$$
m = O\left(\frac{t^2\max{\Norm {H_1}, \Norm {H_2}}^2}{\varepsilon}\right)
$$
因为 $H_1, H_2$ 都是多项式，所以这里也是多项式。

另外还有别的乘积公式，比如

定理 5.1.2 (Trotter-Suzuki formula).
$$
\Norm{\left(e^{-iH_1t/2m}e^{-iH_2t/m}e^{-iH_1t/2m}\right)^m - e^{-i(H_1 + H_2)t}} = O\left(\frac{t^3}{m^2}\right)
$$
证明和上面如出一辙。

对于高维的情形，我们也有
$$
e^{-i(H_1 + \cdots + H_k)t} = \lim_{m\rightarrow \infty}\left(e^{-iH_1t/m}\cdots e^{-iH_k t/m}\right)^m
$$
对于 $k$-local Hamiltonian，其求和项只有最多 $\binom nk$ 项，当 $k = O(1)$ 时，这是 $n$ 的多项式级别。至此我们证明了

定理 5.1.3. $O(1)$-local Hamiltonian 可以被高效模拟。

稀疏 Hamiltonian 模拟

称一个 Hamiltonian 是 $d$-sparse 的，若其每行只有 $d$ 个非零位置。

显然 $k$-local Hamiltonian 是 $2^k\binom nk$-sparse 的。在 $k = O(1)$ 时，这是 $n$ 的多项式级别。

考察 $d$-sparse 的几何意义。注意 Hamiltonian 都是 Hermit 矩阵，所以是对称的，相当于给出了一个每个点度数都不超过 $d$ 的无向图。

命题. 给定一个度数不超过 $d$ 的二分图，可以将其分解为 $d^2$ 个二分图之和。

证明 5.2.1. 给每个点的邻居顶一个顺序。对边 $(u, v)$，假设 $v$ 是 $u$ 的第 $i$ 个邻居，$v$ 是 $u$ 的第 $j$ 个邻居，那么将此边加入第 $id+j$ 个图。

通过下面的办法将一般图的情形约减到二分图：对于 $d$-sparse 的 $H$，$X\otimes H$ 是 $d$-sparse 二分图。而
$$
\begin{aligned}
e^{-(X\otimes H)t} &= I\otimes \left(\sum_{i=0}^\infty\frac{(-it)^{2i}H^{2i}}{(2i)!}\right) + Z\otimes \left(\sum_{i=0}^\infty\frac{(-it)^{2i+1}H^{2i+1}}{(2i+1)!}\right)
\end{aligned}
$$
注意到 $I\ket + = Z\ket + = \ket +$，因此
$$
e^{-i(X\otimes H)t}\ket +\ket \psi = \ket +\otimes e^{-iHt}\ket \psi
$$
用一个辅助比特即实现 $H$ 的模拟。根据乘积公式，我们只需要能做 $1$-sparse Hamiltonian 即可。

假设对于 $1$-sparse Hamiltonian，我们可以查它某一行是哪一个位置非零，以及对应的位置，用如下的 oracle 给出：
$$
U\ket{x, 0, 0} = \ket{x, v(x), H_{x, v(x)}}
$$
因为 Hamiltonian 是 $1$-sparse 的，我们将其放在每条边连接的两个点张成的子空间里考虑。那么此时
$$
H|_{\langle\ket i, \ket{v_i}\rangle} = \begin{pmatrix}
0 & z \\
\bar z & 0
\end{pmatrix} \Rightarrow e^{iHt} |_{\langle\ket i, \ket{v_i}\rangle} = \cos (t|z|) I - i\frac{\sin(t|z|)}{|z|} H | _{\langle\ket i, \ket{v_i}\rangle}
$$
在子空间上是相位旋转。下面的结论不保证正确：

引理 5.2.2. 如果有 $SU(2)$ 上的酉变换 $U$，就用 $O(1)$ 个门可以实现：
$$
\ket a\ket b\ket v \mapsto \ket a\ket b \widehat U\ket v
$$
其中 $\widehat U$ 是唯一的线性映射使得 $\widehat U = U\eta$，其中 $\eta : \ket a\ket b\mapsto \ket 0, \ket b\ket a\mapsto 1$。

证明. 感觉如果存在一个 unitary 能够实现 $\ket a\ket b\ket 0\mapsto \ket a\ket b\ket{[a = b]}$，那么一切都好起来了。这个 unitary 只要有 $n$-qubit Toffoli 好像就可以了。

于是我们可以实现 $\widehat H$ 和 $\widehat T$ 以及受控的这两个门。根据 Solovay-Kitaev 定理，${H, T}^l$ 是旋转变换的 $\varepsilon$-net（其中 $l$ 是 $O({\rm poly}\log 1/\varepsilon)$ 级别的），这表明我们可以制备一条长度为 $2l$ 的 $\widehat H, \widehat T$ 门阵列，然后用 Solovay-Kitaev 定理中的构造算法判断 $e^{-iH(z)t}$ 对应的是哪个序列，从而实现高效模拟。

总算法如下：

• 对于读入的 $\sum_i a_i\ket{x_i}$：
• 作用 $U$ 得到 $\sum_i a_i\ket{x_i}\ket{v(x_i)}\ket{H_{x_i, v(x_i)}}$。
• 作用上面谈到的受控旋转得到

因为我不知道 Solovay-Kitaev 有没有给出构造 / 构造算法复杂度是多少，所以不确定上面的做法对不对。但想了下好像也只能这么干了。

连续时间量子游走

考虑一个图 $G$ 的 Laplace 矩阵 $L$，考虑一个“扩散”过程
$$
\frac{\mathrm{d}}{\mathrm{d}t}\mathbf{p} = L\mathbf{p}
$$
那么这个方程的解显然就是
$$
\mathbf{p}(t) = e^{Lt}\mathbf{p}(0)
$$
这个方程长得和薛定谔方程很像。薛定谔方程的解是
$$
\ket{\psi(t)} = e^{-iHt}\ket{\psi(0)}
$$
只差了一个 $i$，但是有本质不同，因为容易证明：

1. $e^{Lt}$ 是一个随机矩阵，保向量的 $l_1$ 范数。
2. $e^{-iLt}$ 是一个酉矩阵，保向量的 $l_2$ 范数。

在经典情况下，$\mathbf{p}$ 快速趋近于均匀分布。在 $[1, T]$ 内随机一个时间，过这一段时间后观测到某个点 $v$ 的概率接近 $1/v$。但是在量子情况下，这个概率是
$$
\begin{aligned}
p_{a\rightarrow b}(T) &= \frac{1}{T}\int_{0}^T|\bra b e^{-iHt}\ket a|^2\mathrm{d}t \\
&=\frac 1T\int_0^T\bra ae^{iHt}\ket b\bra be^{-iHt}\ket a\mathrm{d}t \\
&= \frac 1T\int_0^T\sum_{\lambda, \lambda’}e^{-i\lambda t}\braket{b}{\lambda}\braket{b}{\lambda}e^{i\lambda’ t}\braket{a}{\lambda’}\braket{a}{\lambda’}\mathrm{d}t \\
&= \sum_{\lambda, \lambda’} \braket{b}{\lambda}\braket{b}{\lambda}\braket{a}{\lambda’}\braket{a}{\lambda’}\int_{0}^T e^{-i(\lambda’ - \lambda)t}\mathrm{d}t
\end{aligned}
$$
假设 $H$ 的特征值是非简并的，那么式子可以拆成
$$
\sum_{\lambda}|\braket{a}{\lambda}\braket{b}{\lambda}|^2 + \sum_{\lambda\ne \lambda’}\braket{b}{\lambda}\braket{\lambda}{a}\braket{a}{\lambda’}\braket{\lambda’}{b}\frac{1 - e^{-i(\lambda - \lambda’)T}}{i(\lambda - \lambda’)T}
$$
后面一项被 $2/(\min(\lambda - \lambda’)T)$ 控制，接下来你可以看到第一项其实非常大。

---

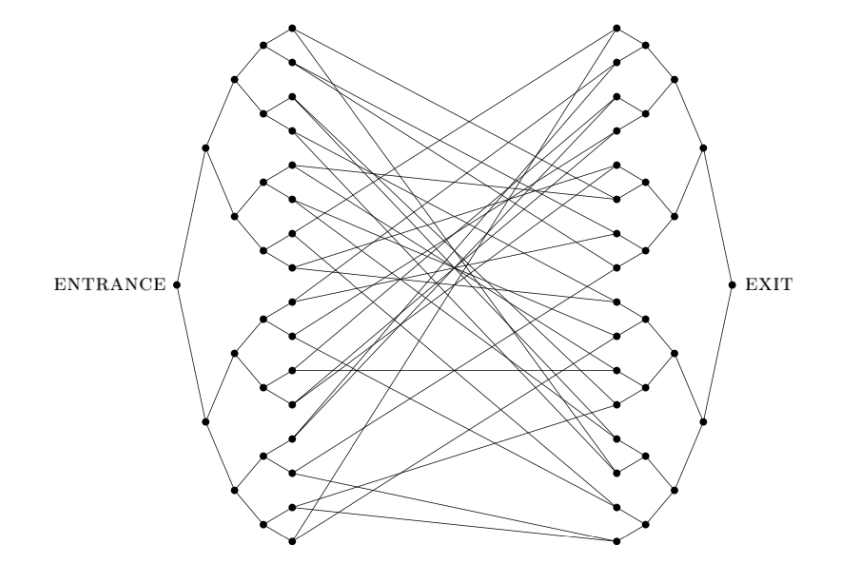
下面的问题称作胶合树问题：

给定一个胶合树

和起点编号，每次可以询问邻居，目标是输出 EXIT 的编号。

假设给定了树上随机游走的 oracle：
$$
A\ket x = \frac{1}{\sqrt{|\mathrm{Neighbor}(x)|}}\sum_{y\in \mathrm{Neighbor}(x)}\ket y
$$
注意到树有对称性，因此定义
$$
\ket{\mathrm{col}_j} = \frac{1}{\sqrt{N_j}} \sum_{dis(a, \text{ENT}) = j}\ket a
$$
简单计算得到 $\mathrm{col}$ 之间的转移概率为：

可以证明胶合树的邻接矩阵在 $\langle\mathrm{col}_i\rangle$ 下特征值非简并，且任意两个特征值之间的差都是至少 $\Omega(n^{-3})$ 的，于是套上之前的分析，有
$$
p_{\mathrm{ENT}\rightarrow\mathrm{EXIT}}(\infty) = |\braket{\mathrm{ENT}}{\lambda}\braket{\mathrm{EXIT}}{\lambda}|^2
$$
注意这个图非常对称，这启发我们可能 $\braket{\mathrm{ENT}}{\lambda}$ 和 $\braket{\mathrm{EXIT}}{\lambda}$ 之间相差不多。考虑一个反射
$$
R : \ket{\mathrm{col}_{j}} \mapsto \ket{\mathrm{col}_{2n + 1 - j}}
$$
则 $R$ 只有 $\pm 1$ 的特征值，其特征向量为 $\frac{1}{\sqrt 2}(\ket{\mathrm{col}_j}\pm \ket{\mathrm{col}_{2n + 1 - j}})$，且 $R$ 和 $A$ 是交换的。那么对于 $A$ 的所有特征向量 $\ket\lambda$ 都有
$$
AR\ket\lambda = RA\ket\lambda = \lambda R\ket\lambda
$$
因为 $A$ 的特征值非简并，但你找到了 $R\ket\lambda$ 和 $\ket\lambda$ 都是 $A$ 的特征向量，因此只能有 $\ket \lambda$ 是 $R$ 的特征向量，特征值为 $\pm 1$。这样一来，它必然和 $\ket{\mathrm{ENT}}\mp \ket{\mathrm{EXIT}}$，从而
$$
\braket{\mathrm{ENT}}{\lambda} = \pm\braket{\mathrm{EXIT}}{\lambda}
$$
继续化简从 $\mathrm{ENT}$ 走到 $\mathrm{EXIT}$ 的概率：
$$
\begin{aligned}
p_{\mathrm{ENT}\rightarrow\mathrm{EXIT}}(\infty) &= \sum_{\lambda}(|\braket{\mathrm{ENT}}{\lambda}|^2)^2 \\
&\geq \frac{1}{2n + 2}\left(\sum_{\lambda}|\braket{\mathrm{ENT}}{\lambda}|^2\right)^2 = \frac{1}{2n + 2}
\end{aligned}
$$
容易证明余下的东西
$$
\begin{aligned}
&\sum_{\lambda\ne \lambda’}\braket{\mathrm{EXIT}}{\lambda}\braket{\lambda}{\mathrm{ENT}}\braket{\mathrm{ENT}}{\lambda’}\braket{\lambda’}{\mathrm{EXIT}} \\
\leq& \frac{2}{T\min(\lambda - \lambda^2)}\sum_{\lambda, \lambda^2} |\braket{\mathrm{EXIT}}{\lambda}|^2|\braket{\mathrm{ENT}}{\lambda’}|^2 \\
=& O\left(\frac{n^3}{T}\right)
\end{aligned}
$$
因此取 $T = Cn^4$，就可以以 $O(n^{-1})$ 概率成功。只需要重复 $n$ 次，就可以高概率成功。

另外注意 $A$ 是一个 $3$-sparse 的 Hamiltonian，所以 $A$ 的模拟式多项式级别的，总复杂度也是多项式的。

对比经典情况，你只能硬走，转移概率大概是

基本上是一直在中间荡来荡去。走到 $\mathrm{EXIT}$ 的期望时间式指数级的。