【Under Construction】应用线性代数学习笔记 (1) 无结构搜索
Abstract. 实际上是量子计算课程的学习笔记。但是在我对底层原理有充分理解之前,我会将我学的东西称为“应用线性代数”。
本片
Grover’s Algorithm
我们期望解决下面所述的无结构搜索问题:
问题. 给定一个函数 $f : [n] \rightarrow \{0, 1\}$,包装成一个 oracle:
$$
|x, z\rangle \xmapsto{U_f} |x, z \oplus f(z)\rangle
$$
搜索其中的一个 $x$,满足 $f(x) = 1$。
首先考虑使用 phase kickback 技巧:
$$
|x, -\rangle \xmapsto{U_f \otimes I} (-1)^{f(x)}|x, -\rangle
$$
这个操作(带有一个辅助比特)成为一次 phase query。考虑这个操作作用在一个均一叠加态 $|\psi\rangle = 1 / \sqrt{n} \sum_{x = 1}^n |x\rangle$ 上:
$$
|\psi\rangle\xmapsto{\text{phase query}} \left(\sum_{x:f(x) = 0}|x\rangle\right) - \left(\sum_{x:f(x) = 1}|x\rangle\right)
$$
这个操作形如某种“反射”。Grover 算法的出发点是,用两种“反射”构造“旋转”,将均一叠加态转到 $f(x) = 1$ 的方向。
首先考虑只有一个元素 $w$ 使得 $f(w) = 1$ 的情况。那么上述的 phase query 写成酉矩阵就是
$$
U = I - 2|w\rangle\langle w|
$$
接下来定义($\psi$ 是均一叠加态)
$$
V = 2|\psi\rangle\langle\psi| - I
$$
我们来制备此门。注意为了实现类似于分支判断的操作,受控门是一个很好的选择,但是受控门对叠加态并不友好。所幸我们注意到
$$
V = H^{\otimes m}(2|0^m\rangle\langle0^m| - I)H^{\otimes m}
$$
因此下图用 $O(\log n)$ 个门制备了该门。
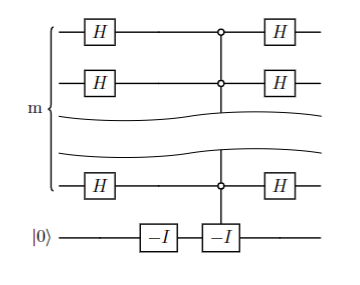
万事俱备。Grover 算法的完整过程如下:
- 制备均一叠加态 $|\psi\rangle$($O(\log n)$ 个门)
- 重复 $t = \pi / 4\sqrt{n}$ 次
- 作用 $U$。
- 作用 $V$。
- 测量。
做一些简单的计算:
$$
\begin{align}
U|\psi\rangle &= |\psi\rangle - \frac{2}{\sqrt n}|w\rangle \\
U|w\rangle &= -|w\rangle \\
V|\psi\rangle &= |\psi\rangle \\
V|w\rangle &= \frac{2}{\sqrt n} |\psi\rangle - |w\rangle
\end{align}
$$
因此 $|\psi\rangle, |w\rangle$ 生成 $U, V$ 下的不变子空间。方便起见,我们将这组基 Schmidt 正交化为 $|w\rangle, |w^\perp\rangle$,其中
$$
|w^\perp\rangle = \frac{|\psi\rangle - \langle w|\psi\rangle|w\rangle}{\parallel |\psi\rangle - \langle w|\psi\rangle|w\rangle\parallel}
$$
于是(假设 $\theta = \arcsin \frac{1}{\sqrt n}$)
$$
\begin{align}
|\psi\rangle &= \frac{1}{\sqrt n}|w\rangle + \sqrt{1 - \dfrac{1}{n}}|w^\perp\rangle \\
&= \sin\theta |w\rangle + \cos\theta|w^\perp\rangle
\end{align}
$$
现在可以方便地在 $|w\rangle, |w^\perp\rangle$ 下研究 $U, V$ 的矩阵表示,我们将看到它正是平面内旋转 $2\theta$ 度:
$$
U = \begin{pmatrix}
-1 & 0 \\
0 & 1
\end{pmatrix}, V = \begin{pmatrix}
-\cos 2\theta & \sin 2\theta \\
\sin 2\theta & \cos 2\theta
\end{pmatrix},
VU = \begin{pmatrix}
\cos 2\theta & \sin 2\theta \\
-\sin 2\theta & \cos 2\theta
\end{pmatrix}
$$
因此
$$
(VU)^t|\psi\rangle = \sin (2t + 1)\theta|w\rangle + \cos(2t + 1)\theta|w^\perp\rangle
$$
如果在标准正交基下测量,想要使得 $w$ 的出现概率尽可能大,就要使得 $(2t + 1)\theta \rightarrow \frac{\pi}{2}$,即 $t\simeq \frac{\pi}{4}\sqrt n$。