常微分方程(1.5)应用举例
Abstract. 本文讨论几个拥有前置知识初等积分法之后可以解决的问题。解决问题的过程中用到了一些建模技巧和神秘手法,具有一些学习价值。此外后面几个关于生态的模型导出的结果是富有趣味和现实意义的,可供消遣。
等角轨线
给定由方程
$$
\Phi(x, y, c) = 0
$$
确定的以 $c$ 为参数的曲线族,求另一个曲线族
$$
\Psi(x, y, k) = 0
$$
满足其中每一条曲线和 $(45)$ 中每一条曲线相交成定角 $\alpha\in \left(-\frac \pi 2, \frac \pi 2\right]$。此时 $(46)$ 称为 $(45)$ 的等角轨线族;若 $\alpha = \frac \pi 2$ 称为正交轨线族。
先进行一些通用的推导。首先有
$$
\begin{cases}
\Phi(x, y, c) = 0 \\
\Phi_{, x}(x, y, c)\mathrm{d}x + \Phi_{, y}(x, y, c)\mathrm{d}y = 0
\end{cases}
$$
从中第一行中还原出 $c$,然后代入第二行中得到
$$
\frac{\mathrm{d}y}{\mathrm{d}x} = -\frac{\Phi_{, x}(x, y, c(x, y))}{\Phi_{, y}(x, y, c(x, y))}
$$
简便起见,将 RHS 记作 $H(x, y)$,即曲线族 $(45)$ 在 $(x, y)$ 点的斜率。那么曲线族 $(46)$ 的计算归结为求解下面两个微分方程之一:
$$
\tan \alpha = \frac{y’ - H(x, y)}{1+y’H(x, y)}
$$
若 $\alpha \ne \frac{\pi}{2}$,或者当 $\alpha = \frac{\pi}{2}$ 时
$$
y’ = -\frac 1 {H(x, y)}
$$
例子 1.1. 求抛物线族 $y = cx^2$ 的正交曲线族。
求解.
首先利用下列方程解出原曲线族在每一点处的斜率 $H(x, y)$:
$$
\begin{cases}
y = cx^2 \\
y’ = 2cx
\end{cases} \color{blue} \Rightarrow y’ = \frac{2y}{x}
$$
故正交曲线族需要满足
$$
\frac{\mathrm{d}y}{\mathrm{d}x} = -\frac{x}{2y}
$$
这是一个简单的分离变量方程,解出
$$
x^2 + 2y^2 = k^2
$$
为同心椭圆族。
Riccati 方程
形如
$$
\frac{\mathrm{d}y}{\mathrm{d}x} = a(x)y^2 + b(x)y + c(x)
$$
其中 $a, b, c$ 是某区间上的连续函数,$a(x)\not\equiv 0$。有定理
定理 2.1. 当 $a(x)\equiv a_0, b(x)\equiv 0, c(x) = c_0x^m$ 时,当且仅当 $m = 0, -2, \frac{-4k}{2k+1}, \frac{-4k}{2k-1}$ 时可以用初等积分法求解。
我们现在的技术不足以证明必要性。但是对于充分性的前两种情况,需要知道当 $m=0$ 时方程是分离变量的,当 $m=-2$ 时换元 $u=xy$ 后得到的方程是分离变量的。
所幸这个方程在知道至少一个解之后可以方便地求解。
定理 2.2. 若已知 $\phi(x)$ 是 $y’ = a(x)y^2 + b(x)y + c(x)$ 的解,那么其它解可以通过解 Bernoulli 方程
$$
y’ = a(x)y^2 + (2\phi(x)a(x)+b(x))y
$$
推得。(事实上这里的 $y$ 解出另一个解和 $\phi(x)$ 的差)
证明.
已知条件指出
$$
\phi’(x) = a(x)\phi^2(x) + b(x)\phi(x) + c(x)
$$
假设 $\psi(x)$ 也是解,即
$$
\psi’(x) = a(x)\psi^2(x) + b(x)\psi(x) + c(x)
$$
将两式做差得到
$$
(\psi(x) - \phi(x))’ = a(x)(\psi(x) +\phi(x))(\psi(x) - \phi(x)) + b(x)(\psi(x) - \phi(x))
$$
可知任意两个解的差值 $\psi(x) - \phi(x)$ 满足下列微分方程:
$$
y’ = a(x)(y + 2\phi(x))y + b(x)y
$$
也就是
$$
y’ = a(x)y^2 + (2\phi(x)a(x) + b(x))y
$$
这是一个 Bernoulli 方程,可以简单地求解。
我们求解一下这个 Bernoulli 方程,顺带复习简单微分方程的解法,依照惯用手法两边除掉 $y^2$ 并换元 $u = y^{-1}$:
$$
u’(x) + (2\phi(x)a(x)+b(x))u(x) + a(x) = 0
$$
然后用经典手法两边乘上 $\exp\left(\int_{x_0}^x2\phi(t)a(t)+b(t)\mathrm{d}t\right)$ 后换元 $v = \exp\left(\int_{x_0}^x 2\phi(t)a(t)+b(t) \mathrm{d}t\right) u(x)$ 得到
$$
v’(x) + a(x)\exp\left(\int_{x_0}^x 2\phi(t)a(t)+b(t) \mathrm{d}t\right) = 0
$$
解出
$$
v(x) = c - \int_{x_0}^x a(t)\exp\left(\int_{x_0}^t 2a(s)\phi(s)+b(s)\mathrm{d}s\right)\mathrm{d}t
$$
进而
$$
y = \exp\left(\int_{x_0}^x 2\phi(t)a(t)+b(t) \mathrm{d}t\right)\left(c - \int_{x_0}^x a(t)\exp\left(\int_{x_0}^t 2a(s)\phi(s)+b(s)\mathrm{d}s\right)\mathrm{d}t\right)
$$
定理 2.3. 若 $\phi_1(x), \phi_2(x)$ 是 $y’ = a(x)y^2 + b(x)y + c(x)$ 的解,那么该方程的任意解 $y$ 均满足
$$
\frac{y - \phi_1(x)}{y - \phi_2(x)} = c\exp\left(\int_{x_0}^x a(t)(\phi_2(t) - \phi_1(t))\mathrm{d}t\right)
$$
其中 $c$ 是常数,取值范围在诸解的公共存在区间中。
证明.
已知 Ricatti 方程的两个解的差值可以用一个 Bernoulli 方程表示:
$$
(y - \phi_i(x))’ = a(x)(y - \phi_i(x))^2 + (2\phi(x)a(x) + b(x))(y - \phi_i(x))
$$
现在我们尝试用这个关系式比较对称地构造欲证明等式的左侧,发现:
$$
\left(\ln \frac{y - \phi_1(x)}{y - \phi_2(x)}\right)’ = a(x)(\phi_2(x) - \phi_1(x))
$$
解出
$$
\frac{y - \phi_1(x)}{y - \phi_2(x)} = c\exp\left(\int_{x_0}^x a(t)(\phi_2(t) - \phi_1(t))\mathrm{d}t\right)
$$
我怀疑书上这里错了一个符号。
推论 7.2.4. 假设 $\phi_1(x), \phi_2(x), \phi_3(x)$ 是原方程的三个不同解,那么方程任意解满足
$$
\frac{y - \phi_1(x)}{y - \phi_2(x)} \big{/} \frac{\phi_3(x) - \phi_1(x)}{\phi_3(x) - \phi_2(x)} = c
$$
人口模型
基于下面两个基本假设对种群数量进行建模:
- 不存在迁入迁出。
- 每个个体具有相同死亡或繁殖机会。
记当前种群数量为 $N(t)$。
附加假设单位时间出生率减去死亡率恒定为 $r$,有如下关系式
$$
N(t + \Delta t) = N(t) + rN(t)\Delta t
$$
采用一个同名的连续函数来拟合这个 $N(t)$,并令 $\Delta t\rightarrow 0$ 立即得到
$$
N’(t) = rN(t)
$$
配上边界条件,这表明 $N(t) = N_0\exp r(t-t_0)$。这正是众所周知的 J 型增长曲线,称为 Malthus 模型。
然而事实上种群数量净增长率可能是一个和种群数量负相关的函数,于是附加假设 $r(t) = r_0 - r_1N(t)$,则
$$
N’(t) = (r_0 - r_1N(t))N(t)
$$
解得
$$
N(t) = \frac{Cr_0\mathrm{e}^{r_0(t-t_0)}}{1+Cr_1\mathrm{e}^{r_0(t-t_0)}}
$$
配上初值条件 $N(t_0) = N_0$ 解出 $C = \frac{N_0}{r_0-N_0r_1}$,带入得到
$$
N(t) = \frac{N_0r_0\mathrm{e}^{r_0(t-t_0)}}{r_0+N_0(r_1\mathrm{e}^{r_0(t-t_0)}-1)}
$$
这正是所谓的 Logistic 曲线,也就是 S 型增长曲线。其有一条渐近线
$$
\lim_{t\rightarrow +\infty} N(t) = \frac{r_0}{r_1}
$$
Volterra 系统
本节考虑两类捕食关系的物种,假设
- A 只以 B 为食
- B 食物充足
进一步假设两物种的增长率关于另一者都是线性的,于是
$$
\frac{\mathrm{d}x}{\mathrm{d}t} = (-a + by)x, \frac{\mathrm{d}y}{\mathrm{d}t} = (c - dx)y
$$
先消去参数 $t$。
$$
\frac{\mathrm{d}y}{\mathrm{d}x} = \frac{(c-dx)y}{(-a+by)x}
$$
Remark. 这里直接乘除方程的理论依据是
- 方程的解是存在的。
- 解 $x = x(t)$ 的反函数存在。
- 链式法则。
解出
$$
dx + by - c\ln x - a\ln y = C
$$
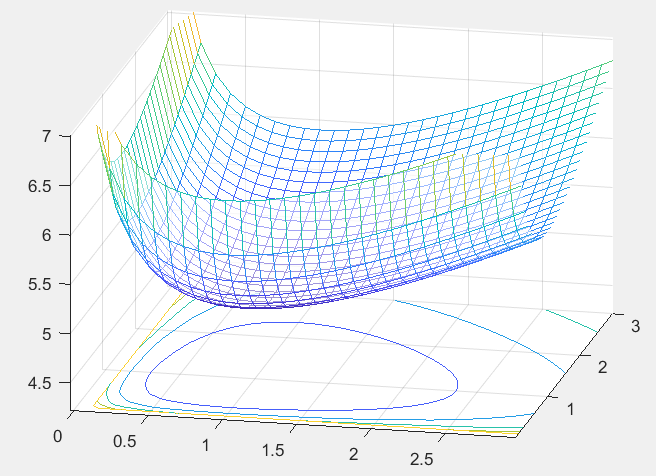
令 $F(x, y) = dx + by - c\ln x-a\ln y$,求 $F(x, y)$ 的前两阶导数
$$
\frac{\partial F}{\partial x} = d - \frac{c}{x},
\frac{\partial F}{\partial y} = b - \frac{a}{y},
\frac{\partial^2 F}{\partial x^2} = \frac{c}{x^2},
\frac{\partial^2 F}{\partial y^2} = \frac{a}{y^2},
\frac{\partial^2 F}{\partial x\partial y} = 0
$$
发现 $F(x, y)$ 的 Hessian 总是正定,于是对于绝大多数 $C$,$F(x, y) = C$ 是凸曲线。
其次我们发现最低点总是 $F(x, y) = C$ 所围成区域 $\mathcal{D}(C)$(i.e. ${(x, y) : F(x, y)\leq C}$)的内点。于是可以取完全包含于 $\mathcal{D}(C)$ 的开圆,在开圆中可以接一个矩形,表明存在某个 $\varepsilon > 0, || (x’(t), y’(t)) || > \varepsilon$ 总是成立。
经过一些琐碎的讨论(可能需要结合初值问题解的唯一性)可以证明本方程所有的解都是周期解(当然有一个平凡的常数解 $x \equiv \frac{c}{d}, y \equiv \frac{a}{b}$)。
Remark. 本人的做法路径为取 $P = \left(\frac{c}{d}, \frac{a}{b}\right)$ 为一基准点,令 $\theta$ 为 $P$ 到 $(x(t), y(t))$ 的极角(由于曲线的凸性,这里将存在一个以 $2\pi$ 周期内的一一对应),然后证明 $\mathrm{d}\theta / \mathrm{d}t$ 有大于 $0$ 的下界(类似于证明 $\inf ||(x’(t), y’(t))|| > 0$),进而显然存在 $t$,$\theta = 2\pi$。此后只需用存在唯一性定理验证周期性确实成立即可。
至此我们还没有学过存在唯一性定理的严格表述,因此这是一个可能的漏洞。
现在假设 $T_C$ 是常数 $C$ 对应解的周期。我们将计算此时种群数量的期望值,简单计算发现用广义积分计算和用一周期计算等价。于是我们对原始方程稍作变形后两边同时从 $0$ 积到 $T_K$,得到:
$$
\int_0^{T_C}\frac{\mathrm{d}x}{x} = \int_0^{T_C} (-a+by)\mathrm{d}x
$$
化简得到
$$
\frac{1}{T_C}\int_0^{T_C} y(t)\mathrm{d}t = \frac{a}{b}
$$
另一边同理,不再抄写。
最后考虑一个趣味问题,如果此时同时对两边做一个外加的小捕捉操作,使得方程组变成下式,两种群的种群数量期望值如何变化?
$$
\frac{\mathrm{d}x}{\mathrm{d}t} = (-a - \varepsilon + by)x, \frac{\mathrm{d}y}{\mathrm{d}t} = (c - \varepsilon - dx)y
$$
重新计算可以知道
$$
\mathbb{E}(x) = \frac{c - \varepsilon}{d}, \mathbb{E}(y) = \frac{a + \varepsilon}{b}
$$
可知捕食者期望数量减少,被捕食者期望数量增加。