一些逻辑话题:如何证明自然演绎系统的一致性、完备性,以及直觉主义逻辑
Abstract. 本文讨论了几个形式系统的语法和语义之间联系的问题,包括证明自然演绎系统的一致性和完备性,以及直觉主义逻辑中不能推导出 $(\neg\neg P)\rightarrow P$。阅读本文需要的对数理逻辑的理解大概与清华大学出版社的“数理逻辑与集合论”前三章一致,如果没有相关知识可以参考这篇笔记。但本文不采用其中定义的公理系统和证明方式,这点在“声明与记号”中有所说明。
声明和记号
在前面两节当中,我们采用的形式系统是Dirk van Dalen, Logic and Structure(Fifth Edition), Springer(2004) 2.4 节定义的自然演绎。不同于国内教材中常见的将证明过程写作有序列表的形式,我们的证明均写作树形。系统的语义仍然采用众所周知的布尔代数来表示。
定义 1.1. 对于 $m : \mathbf{PROP}\rightarrow \{0, 1\}$(这样的映射 $m$ 称为模型),若命题 $\phi$ 中的原子命题 $p_1, …, p_n$ 均以 $m(p_1), …, m(p_n)$ 赋值,在布尔代数当中能够推出 $\phi$ 的真值为 $1$,则称
$$
m\vDash \phi
$$
定义 1.2. 考虑命题 $\phi_1, …, \phi_n$ 和命题 $\psi$,若对于任意的模型 $m$,一旦 $m\vDash \phi_i$ 均成立则 $m\vDash \psi$ 也成立,则称
$$
\phi_1 \cdots \phi_n \vDash \psi
$$
定义 1.3. 考虑命题 $\phi_1, …, \phi_n$ 和命题 $\psi$,如果存在一个自然演绎系统的证明树推导出了 $\psi$,其中所有未被 $\rightarrow I$ 推理取消的叶子恰为 $\phi_1, …, \phi_n$,则称
$$
\phi_1 \cdots \phi_n \vdash \psi
$$
前面的命题序列若具体内容不重要,通常简写作 $\Gamma$。
例子 1.4. 我们有 $p \vdash q\rightarrow p$,因为存在这样一个证明树:
$$
\dfrac{p \quad [q]_1}{q\rightarrow p}\scriptsize(\rightarrow I_1)
$$
其推导出 $q\rightarrow p$,叶子有 $p, q$,但 $q$ 被 $\rightarrow I$ 推理取消。
通常的一致性和完备性定理是指下面两条定理:
定理 1.5(一致性). 若 $\vdash \phi$ 则 $\vDash \phi$。
定理 1.6(完备性). 若 $\vDash \phi$ 则 $\vdash \phi$。
这无非是对于任意的 $\Gamma$ 都有 $\Gamma \vDash \phi \Leftrightarrow \Gamma \vdash \phi$ 的简单推论,在接下来的两节中我们将对这个形式做证明。这里特别声明我们考虑的所有字符串(命题序列、命题本身、证明树)都是有限长度的。
一致性定理的证明
一致性定理的证明是高度平凡的,只需要对所有的证明树做归纳法,在最后一次推理处验证即可。整个证明都不超过习题难度,因此不写。
完备性定理的证明
兹重申我们要证明的结论是如果
$$
\phi_1 \cdots \phi_n \vDash \psi
$$
则必有
$$
\phi_1 \cdots \phi_n \vdash \psi
$$
现在提取 $(6)$ 中所有出现过的原子命题,记作 $p_1, …, p_m$。
Remark. 现在思考如何将语义上验证和语法上推导联系在一起。此处的突破点是模型 $m$ 到底做了什么事情:事实上模型 $m$ 指定了每个原子命题的真假性。在语法层面模拟这个事情,可以定义出命题集合 $\Gamma = \{\hat p_1, …, \hat p_m\}$,其中 $\hat p_i = p_i$ 或者 $\neg p_i$。因为 $\Gamma$ 事实上枚举了每个命题的真假性,所以存在唯一的模型 $m\vDash\Gamma$。我们是否能验证若 $m \vDash \psi$ 则 $\Gamma \vdash \psi$?
事实上,有
引理 3.1. 考虑命题序列 $\Gamma = {\hat p_1, …, \hat p_m}$,其中 $\hat p_i = p_i$ 或 $\neg p_i$,$p_1, …, p_m$ 为所有的原子命题。此时恰好存在一个模型 $m\models\Gamma$,那么
- 若 $m \models \psi$,则 $\Gamma \vdash\psi$。
- 否则 $\Gamma \vdash \psi\rightarrow \bot$。
证明. 只需对命题 $\psi$ 做结构归纳。原子命题的情形是简单的。
若 $m\models \psi$:
- 若 $\psi = \neg\phi$,那么必然有 $m\not\models\phi$,于是根据归纳假设 $m\vdash\phi\rightarrow\bot$ 即 $m\vdash\psi$。
- …
若 $m\not\models\psi$:
- 若 $\psi = \neg\phi$,那么必然有 $m\models\psi$,于是 $\Gamma\vdash\phi$,容易证明 $\vdash\phi\rightarrow\neg\neg\phi$。
- …
打省略号的部分无非是用惯用的手法做一些琐碎的分类讨论。读者只需知道此思路确实能够证明结论即可。
引理 3.2. 若 $\phi_1 \cdots \phi_n \vDash\psi$,那么任取命题序列 $\Gamma = {\hat p_1, …, \hat p_m}$,其中 $\hat p_i = p_i$ 或 $\neg p_i$,$p_1, …, p_m$ 为所有的原子命题,都有 $\phi_1 \cdots\phi_n, \Gamma\vdash\psi$。
证明. 此时存在唯一的模型 $m$ 使得 $m\vDash \Gamma$。
- 若 $m \vDash \psi$,那么由引理 3.1 直接证毕。
- 否则因为 $\phi_1 \cdots\phi_n\vDash\psi$,必然存在 $i$,$m\not\models\neg\phi_i$,引理 3.1 指出 $\Gamma\vdash\phi_i\rightarrow\bot$。于是 $\phi_1\cdots\phi_n, \Gamma\vdash\bot$。使用 $\bot$ 规则推出 $\psi$。
上面两条引理扫除了证明工作的绝大部分障碍,现有 $2^n$ 种 $\phi_1\cdots\phi_n, \Gamma\vdash\psi$,只需要将 $\Gamma$ 消去即可。
引理 3.3. 对于命题集合 $S$,若 $S, \phi \vdash \psi$ 且 $S, \neg\phi \vdash \psi$,那么 $S\vdash\psi$。
证明.
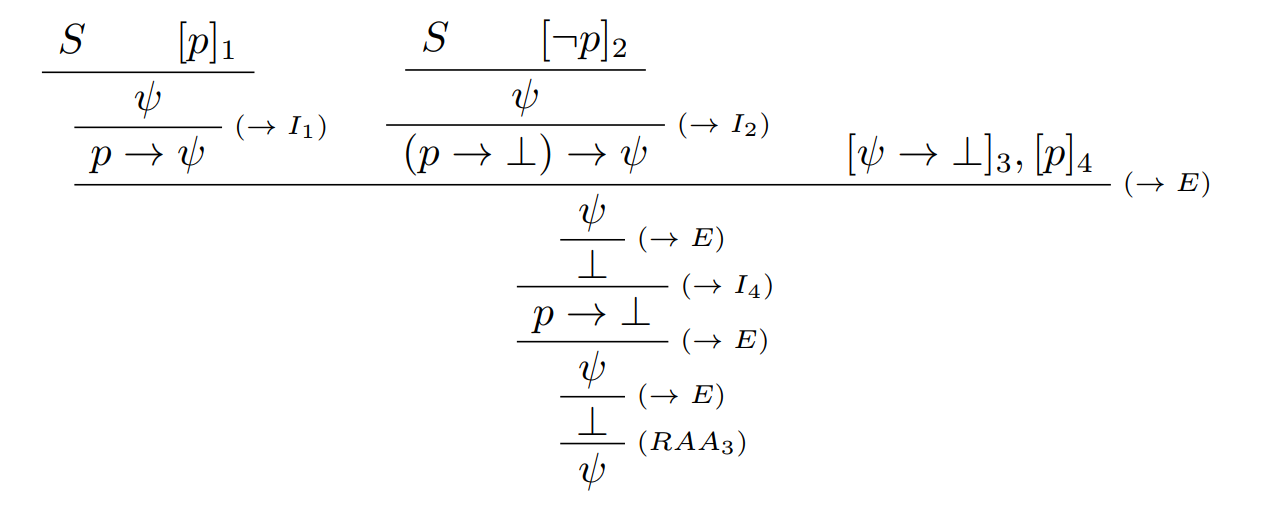
读者不妨自行思考如何基于此引理从 $\phi_1\cdots\phi_n, \Gamma\vdash\psi$ 导出 $\phi_1\cdots\phi_n\vdash\psi$。
直觉主义逻辑:如何证明去掉反证法的系统是不完备的?
我们都知道在 Coq 中不能证明 $\neg\neg P \rightarrow P$(Double Negation Elimination,简称 DNE)或者几个等价的命题,如反证法,排中律,Pierce 律等(参见 Logic in Coq - Software Fundations Vol 1.)。与 Coq 类似的,排中律独立的形式系统称为直觉主义的。那么应当如何证明某个形式系统中无法证明一条结论?
简单考虑自然演绎系统去掉 RAA 组成的形式系统,并尝试证明在其中不能证明 Double Negation Eliminatation。
若只从语法的角度切入这个问题,可以想象的证明方法只有枚举一切的证明树,其难度可想而知。因此我们必须将语义和语法结合起来,于是不难想象这样一条证明路线:
- 为形式系统构造一个新语义(因为布尔代数保证了逻辑就是二值的,排中律必然成立)。
- 证明该形式系统在此语义下是一致的。
- 发现 DNE 在此语义下并不成立。
直觉主义逻辑最知名的语义是如下的 Kripke’s Model:
定义 4.1. 一个 Kripkle’s Model 包含如下资料:偏序集 $W$,映射 $V : W\rightarrow 2^{\mathbf{PROP}}$ 满足若 $u, v\in W, u\leq v$ 则 $V(u)\subseteq V(v)$,配上一个 形如 $(W, V, w), w\in W$ 的三元组 与 命题 之间的二元关系 $\Vdash$。其中:
- $(W, V, w)\Vdash p$ 若 $p\in V(w)$,其中 $p$ 为原子命题。
- $(W, V, w)\Vdash \bot$ 总是不成立。
- $(W, V, w)\Vdash p\wedge q$ 若 $(W, V, w)\Vdash p$ 且 $(W, V, w)\Vdash q$。
- $(W, V, w)\Vdash p\rightarrow q$ 若任给 $v\geq w$,都有一旦 $(W, V, v)\Vdash p$ 则 $(W, V, v)\Vdash q$。
在同构意义下 $W, V$ 显得不太重要,下文我们可能将 $W, V$ 省略不写,将 $(W, V, w)\Vdash \phi$ 简单地记录为 $w\Vdash \phi$。
为了与原来的语法和语义区分,若一个命题 $\phi$ 能在去掉 RAA 的系统中被证明,称 $\vdash_i \phi$。若对于任意的 $W, V, w$ 都有 $(W, V, w)\Vdash \phi$,则称 $\vDash_i\phi$。
定理 4.2. 若 $\vdash_i \phi$ 则 $\vDash_i\phi$,即自然演绎系统去掉 RAA 在 Kripke’s Model 下是一致的。
虽然 Kripke’s Model 比布尔代数稍微抽象一些,但是本定理的证明仍然同布尔代数语义的版本一样简单,所以这里省略不写。至此我们已经可以尝试证明系统不能推出 DNE:
定理 4.3.
$$
\not\vdash_i ((P\rightarrow \bot)\rightarrow \bot)\rightarrow P
$$
并且
$$
\not\vdash_i (((P\rightarrow\bot)\rightarrow\bot)\rightarrow P) \rightarrow\bot
$$
证明. 反之假设 $\vdash_i ((P\rightarrow\bot)\rightarrow\bot)\rightarrow P$。完备性定理指出此时有
$$
\vDash_i ((P\rightarrow\bot)\rightarrow\bot)\rightarrow P
$$
然而我们令 $W = \{\varnothing, {P}\}, V = \mathrm{Id}_W$,可以从左到右地验证下表:
| $w\Vdash$ | $P$ | $P\rightarrow\bot$ | $(P\rightarrow \bot)\rightarrow \bot$ | $((P\rightarrow\bot)\rightarrow\bot)\rightarrow P$ | $\mathrm{DEM}\rightarrow\bot$ |
|---|---|---|---|---|---|
| $\varnothing$ | NO | NO | YES | NO | NO |
| $\{P\}$ | YES | NO | YES | YES | NO |
注意第二行给出 $(W, V, \varnothing)\not\Vdash ((P\rightarrow\bot)\rightarrow\bot)\rightarrow P$,矛盾。上表同样表明 DNE 不能被证伪。明所欲证。
Remark. 我们做的事情看起来很奇怪。用一句批话来说,我们用反证法证明了自然演绎系统去掉反证法之后不能证明反证法。但我们做的事情事实上没有任何问题。
首先,论证一个形式系统的性质必须采用更高级的语言。否则你将无法区分下面两种情况:
- 形式系统是正确的。
- 形式系统能够证明错误的命题,其中包括“自身是正确的”这一条命题。
其次读者不妨区分这两组概念:
- 定理 $p$ 能被证明 / 能被证伪。(i.e. $\vdash p$ 和 $\vdash p\rightarrow\bot$)在直觉主义逻辑中这两者并不是总有一者成立。
- 定理 $p$ 能被证明 / 不能被证明。(i.e. $\vdash p$ 和 $\not\vdash p$)。在人类对 $\vdash$ 的定义下这两者必有一者成立。