Machine Learning (1)(模型选择、线性模型、决策树)
Abstract. 本文是周志华《机器学习》的学习笔记,从中摘要一些没见过或者有意思的东西。
每次卡住了就开一篇新文章。
绪论
在一个多分类问题中,一个损失函数 $L(x, y)$ 被称为 Homogeneous 的,若其满足
$$
\forall x, \sum_i L(x, i) = 1
$$
Theorem 1.1(No Free Lunch, Wolpert 1996). 假设真实的目标函数服从均匀分布,对于 Homogeneous 的损失函数 $\mathcal{L}(\cdot, \cdot)$,任何机器学习算法具有相同的期望泛化性能。
形式化地,此时我们要用一个机器学习算法来拟合 $f : \mathcal{X}\rightarrow \mathbb{Z}/n\mathbb{Z}$,我们的训练集是 $X\subseteq \mathcal{X}$,机器学习算法 $\mathfrak{L}_a$ 可以抽象为经过训练集的训练之后,其以 $P(h | \mathcal{X}, \mathfrak{L}_a)$ 的概率产生函数 $h$。此时该算法的期望泛化性能为
$$
\sum_f P(f) \sum_h P(h | \mathcal{X}, \mathfrak{L}_a) \sum_{\boldsymbol{x}\in \mathcal{X}\setminus X} P(\boldsymbol{x})\mathcal{L}(h(\boldsymbol{x}), f(\boldsymbol{x}))
$$
Proof.
直接进行简单的推导即可:
$$
\begin{align}
&\sum_f P(f) \sum_h P(h | \mathcal{X}, \mathfrak{L}_a) \sum_{\boldsymbol{x}\in \mathcal{X}\setminus X} P(\boldsymbol{x}) \mathcal{L}(h(\boldsymbol{x}), f(\boldsymbol{x})) \\
=&\sum_{\boldsymbol{x}\in \mathcal{X}\setminus X} P(\boldsymbol{x}) \sum_h P(h | \mathcal{X}, \mathfrak{L}_a) \sum_f P(f) \mathcal{L}(h(\boldsymbol{x}), f(\boldsymbol{x})) \\
=&\sum_{\boldsymbol{x}\in \mathcal{X}\setminus X} P(\boldsymbol{x}) \sum_h P(h | \mathcal{X}, \mathfrak{L}_a) \frac{1}{n} \\
=&\frac 1n \sum_{\boldsymbol{x}\in \mathcal{X}\setminus X} P(\boldsymbol{x})
\end{align}
$$
$(4)\Rightarrow (5)$ 用到 $f$ 的均匀分布性质和 $\mathcal{L}$ 的 homogeneous 性质,跳过了枚举 $f(\boldsymbol{x})$ 的值然后交换求和顺序一步。$\square$
这个定理的实际上没有什么道理,因为现实中 $f$ 并非服从均匀分布。从寓意上来讲这个定理告诉我们谈论算法的优劣必须考虑具体的问题。
模型评估与选择
小数据集上一个比较有道理的数据集划分方法:Bootstrapping。
对于一个大小为 $m$ 的初始数据集,做 $m$ 次均匀采样得到训练集,未被采到的划入验证集。
简单分析可以知道这个相当于一个 $\frac{1}{\mathrm{e}}$ 大小验证集的划分,但是每一个元素都有机会出现在训练集中。多次做 Bootstrapping 可以得到多个训练集/验证集,可以用于集成学习。但是需要注意这个做法改变了初始数据集的分布,可能引入估计偏差。
上学期 AI 基础学 Object Detection 的时候有一个很神秘的精度率-召回率图:
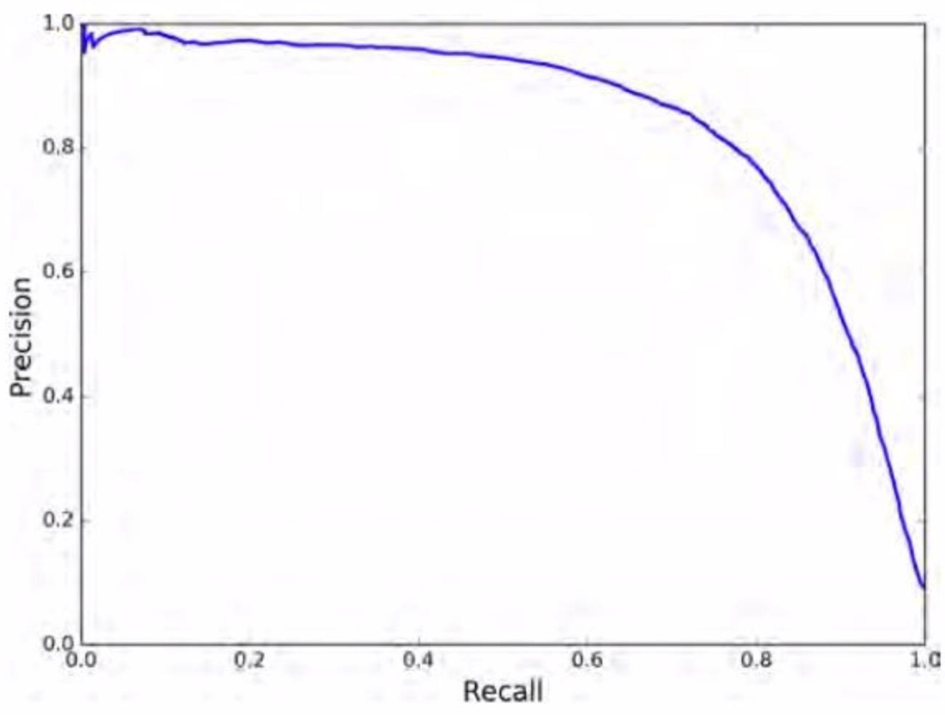
当时不知道此图如何得到,现在简述一下。
这个图是模型进行一次预测之后得到的,目的是为了调整分类为正类的阈值。将阈值设定为不同的值,可以得到不同的精度率和召回率。将这些数据描点连线即可得到上述图表。
得到了这个图之后模型的比较可以基于如下方法:
- 严格优于: $A$ 模型的曲线完全包络了 $B$ 模型的曲线。
- $F_1$: 比较关键字为精度率和召回率的调和平均。
- $F_\beta$: 比较关键字为精度率和召回率依次带上权重 $\beta^2, 1$ 的加权调和平均。
另一种图是召回率 $\frac{TP}{TP+FN}$ - 假阳性率 $\frac{FP}{FP+TN}$ 图(ROC 图),简单计算可以发现阈值从小到大增长的过程中这会是一个从 $(0, 0)$ 到 $(1, 1)$ 的曲线。如果两个算法的 ROC 图之间出现了包含关系,那么可以断言一者完全由于另一者,否则一个比较科学的方法是比较曲线下面积(AUC)。
下面介绍几个所谓的比较检验法。我们不能知道一个模型的泛化误差,但是假设测试集是从数据中均匀采样得到的,那么我们可以从测试误差估计泛化误差。
Binomial Test. 假设一个模型的泛化误差为 $\varepsilon$,测试集大小为 $m$,那么该模型被测出具有测试误差 $\hat{\varepsilon}$ 的概率为
$$
P(\hat{\varepsilon}; \varepsilon) = \binom{m}{\hat{\varepsilon}m}\varepsilon^{\hat{\varepsilon}m}(1-\varepsilon)^{m-\hat{\varepsilon}m}
$$
接下来我们试图放缩 $\varepsilon$ 的上界:即假设 $\varepsilon < \varepsilon_0$。则对于指定的容错率 $\delta$,我们可以找到
$$
\bar{\varepsilon} = \min\left\{\varepsilon ~\Bigg| \sum_{i=\varepsilon m + 1}^m \binom{m}{i}\varepsilon_0^i(1-\varepsilon_0)^{m-i} < \delta \right\}
$$
若 $\hat{\varepsilon} > \bar{\varepsilon}$ 则可以说有 $1-\delta$ 的把握认为 $\varepsilon < \varepsilon_0$ 成立。
Remark. 这段话是书上写的,我并不是很认同, 因为我算了一下总感觉哪个不等号的方向反过来了,他写的 Binomial Test 和正常的 Binomial Test 也不是很像。要么是我哪里看错了。
$t$-Test、McNemar Test、Friedman Test、Nemenyi Test
这部分涉及到一些 $\chi^2$ 分布、$t$ 分布的使用,但是因为我对这两个东西完全不熟悉,所以先跳过这一节的推导,停留在会查表格的程度。
查表格只是一些琐碎的工作,这里不写。
Bias-Variance Decomposition
假设 $D$ 是一个数据集 $\boldsymbol{x}\in D$ 是某一个训练样本,$y_D$ 是其在数据集中的标注。$y$ 为其真实标记(这里 $y_D\ne y$,表示标注错误),$f(\cdot; D)$ 是算法在 $D$ 上拟合到的函数,$\bar f(\boldsymbol{x}) = \mathbb{E}_{D} (f(\boldsymbol{x}; D))$。
假设 $y_D$ 是 $y$ 添加随机噪声 $\varepsilon$ 得到的,其中 $\mathbb{E}[\varepsilon] = 0, \mathrm{D}[\varepsilon] = \sigma^2$,$y$ 和 $\varepsilon$ 独立。学习算法和误差无关,即 $f$ 和 $\varepsilon$ 独立。现在考察数据集上的期望误差:
$$
\begin{align}
\mathbb{E}_{D, \boldsymbol{x}}[(y_D - f(\boldsymbol{x}; D))^2] &= \mathbb{E}_{D, \boldsymbol{x}}[y_D^2] - 2\mathbb{E}_{D, \boldsymbol{x}}[y_D f(\boldsymbol{x}; D)] + \mathbb{E}[f(\boldsymbol{x}; D)^2]
\end{align}
$$
现在逐项化简。
$$
\begin{align}
\mathbb{E}_{D, \boldsymbol{x}}[y_D^2] &= \mathbb{E}_{D, \boldsymbol{x}}[(y + \varepsilon)^2] \\
&= \mathbb{E}_{D, \boldsymbol{x}}[y^2] + 2\mathbb{E}[y]\mathbb{E}[\varepsilon] + \sigma^2 & \color{blue}{\text{($y$ and $\varepsilon$ are independent)}} \\
&= \mathbb{E}_{\boldsymbol{x}}[y^2] + \sigma^2\\
\mathbb{E}_{D, \boldsymbol{x}}[y_D f(\boldsymbol{x}; D)]
&= \mathbb{E}_{D, \boldsymbol{x}}[yf(\boldsymbol{x}; D)] + \mathbb{E}_{D, \boldsymbol{x}}[\varepsilon f(\boldsymbol{x}; D)] \\
&= \mathbb{E}_{D, \boldsymbol{x}}[yf(\boldsymbol{x}; D)] & \color{blue}{\text{($f$ and $\varepsilon$ are independent)}} \\
\mathbb{E}_{D, \boldsymbol{x}}[f(\boldsymbol{x}; D)^2]
&= \mathrm{D}_{D, \boldsymbol{x}}[f(\boldsymbol{x}; D)] + \mathbb{E}_{D, \boldsymbol{x}}[f(\boldsymbol{x}; D)]^2 \\
&= \mathrm{D}_{D, \boldsymbol{x}}[f(\boldsymbol{x}; D)] + \mathbb{E}_{\boldsymbol{x}}[\bar{f}(\boldsymbol{x})]^2
\end{align}
$$
加起来不难得到
$$
\mathbb{E}_{D, \boldsymbol{x}}[(y_D - f(\boldsymbol{x}; D))^2] = \underbrace{\mathbb{E}_{D, \boldsymbol{x}}[(\bar{f}(\boldsymbol{x})-y)^2]}_{bias^2} + \underbrace{\mathrm{D}_{D, \boldsymbol{x}}[f(\boldsymbol{x}; D)]}_{variance} + \underbrace{\sigma^2}_{noise}
$$
书上的推导有一些跳步导致很难看懂,所以我们换了一种做法。
感性理解,起来,模型越复杂,拟合效果越好(bias 越小),但鲁棒性越差(variance 越大),这导致总的训练效果存在一均衡点[1]:
线性模型
LDA, 1936
假设现在欧式空间中有两类、若干数据点,现在要做一条直线,使得两类投影到该直线上之后,区分地尽量开。
到这里给人的感觉就有一点像分类版本的 PCA,在后面给出做法之后我们会发现两者确实很类似。
量化考虑这一件事情。区分的尽量开可以有两个指标:
- 异类点之间的距离尽量大。
- 同类点的方差尽量小。
我们考虑定义下面几个量:
$X_i$ 表示第 $i$ 类点的集合。
$\boldsymbol{\mu}_i$ 表示第 $i$ 类点的均值。
$\Sigma_i$ 表示第 $i$ 类点的协方差矩阵。这个概念有点陌生,我们稍作解释。
$\Sigma_i$ 是一个阶数为空间维数的矩阵,它的计算方法为
$$
\Sigma_i = \sum_{\boldsymbol{x}\in X_i} (\boldsymbol{x} - \boldsymbol{\mu}_i)(\boldsymbol{x} - \boldsymbol{\mu}_i)^T
$$可以用这个矩阵计算这些向量投影到一个子空间 $W$ 上之后的协方差矩阵。假设 $W$ 有一组标准正交基 $\boldsymbol{w}_1, …, \boldsymbol{w}_r$,令 $\mathbf{W} = (\boldsymbol{w}_1, …, \boldsymbol{w_r})$,那么显然有
$$
\Sigma’_i = \mathbf{W}^T \Sigma_i \mathbf{W}
$$而可以用协方差矩阵推知方差:
$$
D_i = \mathrm{tr}(\Sigma_i)
$$
LDA 假设 $\Sigma_i$ 均满秩,其最大化
$$
J = \frac{||\boldsymbol{w}^T\boldsymbol{\mu}_0 - \boldsymbol{w}^T\boldsymbol{\mu}_1||^2}{\boldsymbol{w}^T(\Sigma_0 + \Sigma_1)\boldsymbol{w}}
$$
我们定义 $\mathbf{S}_w = \Sigma_0 + \Sigma_1, \mathbf{S}_b = (\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1)(\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1)^T$ 来简化上式的形式。观察这两个矩阵的形式,$\mathbf{S}_w$ 是正定的,$\mathbf{S}_b$ 是半正定的,并且是投影。我们现在要最大化
$$
J = \frac{\boldsymbol{w}^T\mathbf{S}_b\boldsymbol{w}}{\boldsymbol{w}^T\mathbf{S}_w\boldsymbol{w}}
$$
Claim. 当
$$
\boldsymbol{w} = \mathbf{S}_w^{-1}(\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1)
$$
时,原优化问题取到最优。
书上有基于拉格朗日乘子法的推导,但是很遗憾我们对矩阵求导并不熟悉,因此我们考虑纯线性代数推法。
Derivation.
上面的式子是齐次式,所以下面的讨论中我们将在合理的地方忽略向量的长度。
注意 $\mathbf{S}_w$ 是正定矩阵,因此存在正定矩阵 $\mathbf{C}$ 使得 $\mathbf{S}_w = \mathbf{C}^T\mathbf{C}$。令
$$
\boldsymbol{w_1} = \mathbf{C}\boldsymbol{w}, \mathbf{S_1}_b = (\mathbf{C}^{T})^{-1}\mathbf{S}_b\mathbf{C}^{-1}
$$
那么原式变成了
$$
J = \frac{\boldsymbol{w_1}^{T}\mathbf{S_1}_b\boldsymbol{w_1}’}{||\boldsymbol{w_1}||^2}
$$
这个式子很经典,它的最大值是 $\mathbf{S_1}_b$ 的最大特征值,$\boldsymbol{w_1}$ 取特征向量时取等。
$\dim \mathrm{Im~}\mathbf{S_1}_b = 1$,因此想要得到这个特征值的特征向量,只能在像空间里面找,我们让它乘上一个向量 $\boldsymbol{v}$:
$$
\mathbf{S_1}_b\boldsymbol{v} = \mathbf{C}^{-1}(\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1)\color{red}{(\boldsymbol{\mu}_0 - \boldsymbol{\mu_1})^T\mathbf{C}^{-1}\boldsymbol{v}}
$$
注意红色部分是标量,因此 $\mathbf{C}^{-1}(\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1)$ 是特征向量(你可以验证这一点,将其带入上式,根据 $\mathbf{S}_w$ 的正定性立即得到红色部分不是 $0$),即原最优化问题的解。还原到 $\boldsymbol{w}$ 一侧得到
$$
\boldsymbol{w} = \mathbf{S}_w^{-1}(\boldsymbol{\mu}_0 - \boldsymbol{\mu}_1)
$$
时原问题最优。
这个做法有点太 Adhoc 了。所谓的拉乘做法是添加分母为 $0$ 的条件然后最大化分子。对 $\boldsymbol{w}$ 求偏导之后得到 $\mathbf{S}_b\boldsymbol{w} = \lambda \mathbf{S}_w\boldsymbol{w}$,后面也需要注意到 $\mathbf{S}_b$ 的像是一维的。
考虑 $k$ 分类的 LDA,我们定义
$$
\mathbf{S}_w = \sum_{i=1}^k \Sigma_i, \mathbf{S}_b = \sum_{i=1}^k |X_i|(\boldsymbol{\mu_i} - \boldsymbol{\mu})(\boldsymbol{\mu}_i - \boldsymbol{\mu})^T
$$
这里 $\boldsymbol{\mu}$ 是全局重心。现最大化
$$
\frac{\mathrm{tr}(\mathbf{W}^T\mathbf{S}_b\mathbf{W})}{\mathrm{tr}(\mathbf{W}^T\mathbf{S}_w\mathbf{W})}
$$
Claim. 当且仅当 $\mathbf{W}$ 每一列都为 $\mathbf{S}_w^{-1}\mathbf{S}_b$ 的最大特征值的特征向量时(至少有一列不是 $0$)取最大值。
Proof.
将 $\mathbf{W}$ 写成分块矩阵 $(\boldsymbol{w}_1, …, \boldsymbol{w}_r)$,那么目标等于
$$
\frac{\sum \boldsymbol{w}_i^{T}\mathbf{S}_b \boldsymbol{w}_i}{\sum \boldsymbol{w}_i^{T}\mathbf{S}_w \boldsymbol{w}_i}
$$
注意 $\lambda$ 是最大的特征值,那么首先将整个空间分解成特征子空间的直和 $V = \bigoplus V_{\lambda_i}$,然后将向量 $\boldsymbol{w}$ 分解成不同特征值的特征向量的和 $\boldsymbol{w} = \sum \boldsymbol{w}_i$。于是
$$
\frac{\boldsymbol{w}^T \mathbf{S}_b \boldsymbol{w}}{\boldsymbol{w}^T \mathbf{S}_w \boldsymbol{w}} = \frac{\lambda_i\boldsymbol{w}^T \mathbf{S}_w \boldsymbol{w}}{\boldsymbol{w}^T \mathbf{S}_w \boldsymbol{w}} \leq \lambda
$$
取等仅当 $\boldsymbol{w}\in V_\lambda$。用这个式子对目标放缩即得到答案。$\square$
Remark. 早这么算就屁事没有了。
如果 $\boldsymbol{w}_1, \cdot, \boldsymbol{w}_r$ 取 $V_\lambda$ 的标准正交基,本质上这里相当于将整个空间用 $\mathbf{W}$ 投影到 $V_\lambda$ 里,实现了数据的保持类别区别的降维。
二分类构造多分类
三种方法。
- OvO,学习 $\binom n2$ 个二分类(两两之间),最后输出通过投票产生。
- OvR,学习 $n$ 个二分类(一个和其他),最后输出选置信度最大的。
- RvR,学习 $m$ 组,每一组中将一部分编为正类,一部分编为负类,得到每一类在这 $m$ 次分类中得到的结果 $r_1, …, r_m$。最后输出测试结果 $r$ 在 $r_1, …, r_m$ 中的最近邻(汉明或者欧式)
类别不平衡处理
假设正例个数有 $m_+$ 个,反例个数有 $m_-$ 个。
rescaling 基于数据集从实际情况无偏采样得到的假设,只需
$$
\frac y{1-y} > \frac{m_+}{m_-}
$$即认为是正类。对比原来的式子,只需要给 log odds 乘上 $m_-/m_+$ 即可。
这个做法的问题是其假设不一定对。
undersampling 丢掉多的类。
为了防止丢失信息最好进行集成学习。
oversampling 对于少的类进行反复采样。
如果简单地重复采样会导致过拟合。可以考虑插一下值。
决策树
基本算法
首先考虑信息都是 Category 的情况。
粗略来说就是每次选择一个可以继续分割的节点,选择一个最优的属性,创建儿子节点。
一个节点 $u$ 上样本的集合为 $S_u$,其中有 $k_u$ 个类别的样本,第 $i$ 类占比为 $p_{ui}$,其信息熵记为
$$
\mathrm{Ent}(u) = -\sum_{i=1}^{k_u} p_{ui}\log p_{ui}
$$
熟知这东西越大表明集合越混乱。
假设按照属性 $a$ 划分之后产生的儿子集合为 $\mathrm{son}(u, a)$,那么下面的量(称为信息增益)可以作为比较标准:
$$
\mathrm{Gain}(u, a) = \mathrm{Ent}(u) - \sum_{v\in\mathrm{son}(u, a)} \frac{|S_v|}{|S_u|}\mathrm{Ent}(v)
$$
这个指标导致算法倾向于选择属性较多的类(比如说如果引入一个“编号”类,它会直接去选择编号这一属性),会导致过拟合。所以我们引入一个因子来平衡这个东西:
$$
\mathrm{IV}(u, a) = -\sum_{v\in \mathrm{son}(u, a)} \frac{|S_v|}{|S_u|}\log\frac{|S_v|}{|S_u|}
$$
新的比较标准(称为信息增益率)如下
$$
\mathrm{GainRatio}(u, a) = \frac{\mathrm{Gain}(u, a)}{\mathrm{IV}(u, a)}
$$
实践中发现加入这个量之后会偏好取值较少的类,只能加一些启发式的算法比如先选出信息增益高于平均值的,然后选增益率最大的。
此外还有一个可以衡量集合混乱程度的东西,称为基尼值(组合意义是 uniform sample 两个样本,类别不一致的概率):
$$
\mathrm{Gini}(u) = 1 - \sum_{i=1}^{k_u} p_{ui}^2
$$
因此下面的基尼指数也可以作为比较标准:
$$
\mathrm{GiniIndex}(u, a) = -\sum_{v\in\mathrm{son}(u, a)} \frac{|S_v|}{|S_u|}\mathrm{Gini}(v)
$$
剪枝
防止过拟合。用验证集来估计模型的泛化能力。一般有两种:
- Prepruning. 在要进行一次划分的时候做验证,观察准确率是不是掉了,如果掉了就放弃划分。
- Postpruning. 训练完之后按深度从大到小考察每个节点,如果放弃划分验证准确率变高了就放弃划分。
连续值
显然你只能考虑将节点上的样本的连续值拿出来排序,然后取相邻两个数的中位点 / 某一个数作为划分的阈值,每次把节点裂成两个。
然后你发现目标函数(信息熵 / 基尼指数)关于这个决策点都没有什么好性质,可能既不凸也不单调,最极端的情况只需要考虑正类和反例总和为偶数,且间隔排列的情况,严格来说似乎没有优于枚举的做法。但是如果你的特征选的非常好的话应该不会有这种极端情况,此时可能至少模拟退火之类的局部搜索算法是能用的。
只考虑单变量的决策树只能用一个锯齿来拟合分类边界,想要拟合斜线可以考虑对于多个变量,考虑一个线性的式子作为分类依据:
$$
\sum_{i=1}^t \omega_i v_i + \beta \leq 0
$$
参数是 $\omega_i, \beta$(其实 $\beta$ 换成 $1$ 也没什么问题)。同样的这个东西不凸也不单调,用梯度下降来优化绝对是没有什么道理的,但是局部搜索可能能用。
神经网络
关于 MLP、反向传播的内容是众所周知的,直接跳过。
至少有一个隐藏层的 MLP 是 Universal Approxiator 这个事实很有意思,但是我暂时不会证明。
怎么这一章全是批话,看了跟没看一样。
