Revision | AI 基础（期中）

Abstract. AI 基础复习笔记。背书。

里面有一些不知道有什么道理的批话，均用斜体表出。

• 历史
• Math for AI
  • 最大似然估计（MLE）
  • 最大后验概率（MAP）
  • 信息论
• 机器学习选讲
  • 线性回归
  • 逻辑回归
  • 其他东西
• 神经网络
• CNN
  • 批话
  • 代表性网络
  • 应用
    • Object Detection
    • Image Segmentation
    • Face Recognition
• GAN
  • 经典算法
• RNN
• Transformer
  • 网络结构
  • 预训练模型

历史

1955, Dartmouth 会议提出人工智能一词。

• 初心：有智能的机器。 [Turing, 1948]
  • 任务：定理证明，下棋，说话，看图，像人一样行动，
  • 目标：通用。
  • 路径：将人类智慧输入机器（符号派）、神经网络（连接派），强化学习（行为派）。
• 早期：百花齐放
  • Logical Theorist，1955-1956，数学定理（数学原理）证明，启发式搜索。
  • IBM 深蓝，1985，国际象棋，Minimax 搜索、Alpha-Beta 剪枝。
  • Georgetown 实验，1953-1954，机器翻译（有机化学领域）。
  • ELIZA，1964-1966，对话，关键词打分、查找表。
  • SHRDLU（积木世界），1968-1970，回答并按要求挪动物品（拥有记忆单元），逻辑推理。
  • STRIPS，1971，自动规划问题。
  • Conway Game，1950，模拟生物细胞自我复制。
  • Perceptron，1943，图像识别，单层神经网络。不能解决异或问题。
• 中期：符号主义
  • 自动定理证明：王浩 1958（一阶逻辑），吴文俊（几何）。
  • Dendral（第一个专家系统软件）：有机化学，推理分子组成和结构。
  • MYCIN：识别细菌，推荐抗生素。推理引擎、知识库、不精确推理。
  • 知识库：Cyc，Semantic Network，WordNet $\Rightarrow$ IBM watson。
  • 日本五代机：失败。
• 近期：联结主义
  • AlexNet：CNN（ReLU，Dropout，LRN）
  • AlphaGo：监督学习，强化学习，MCTS。AlphaGo Zero：放弃人类专家经验，从零开始学习。
  • ChatGPT。

Math for AI

Theorem.(Bayes)

$$
p(Y|X) = \frac{p(X|Y)p(Y)}{\sum_Y p(X|Y)p(Y)} \propto p(X|Y)p(Y)
$$

Nomenclatures.

• 后验概率（posterior）：$P(Y|X)$，观察到结果 $X$ 之后的概率。
• 似然（likelihood）：$P(X|Y)$，对于参数设置，观察到数据集的可能性。
• 先验（prior）：$P(Y)$，对参数分布的猜测。

分母称为归一化因子。

最大似然估计（MLE）

假设数据独立同分布，给定一个观测到的数据，求一个参数 $\theta$ 来最大化概率，i.e.

$$
\mathrm{argmax}_\theta \sum_{i=1}^n \log p(x_i | \theta)
$$

Example. 给定一组数据，假设服从正态分布，用 MLE 估计分布。

Hint.

直接求偏导即可。可以解出 $\mu$ 就是本组数据的均值，$\sigma^2$ 就是本组数据的方差。

最大后验概率（MAP）

假设数据独立同分布，给定一个观测到的数据和你对参数 $\theta$ 服从的分布的假设 $p(\theta)$，i.e.

$$
\mathrm{argmax}_\theta \sum_{i=1}^n \log p(x_i | \theta) p(\theta)
$$

信息论

Definition.(KL-divergence)

$$
D_{KL}(P || Q) = \mathbb{E}_{x\sim P} (\log P(x) - \log Q(x))
$$

衡量两个分布之间的差异，根据 Gibss 不等式其总是大于零。感性理解起来这个量表示如果用分布 $Q$ 来解析信息，期望丢失多少信息。

Definition.(Cross Entropy)

$$
H(P, Q) = H(P) + D_{KL}(P || Q)
$$

一般最小化交叉熵和最小化 KL 散度等价。

机器学习选讲

大纲. 机器学习指基于经验的算法的设计与分析使得模型在某些任务上的表现得到提升。

• 任务 监督学习（分类，回归），无监督学习（聚类，密度估计，降维），半监督学习，弱监督学习，强化学习。
• 经验 指训练数据。好的机器学习模型应当不过拟合到训练数据，可以泛化到测试数据。
• 表现 有多种方法进行衡量，数学上反映为最小化某个损失函数（0/1 loss, square loss, cross entropy loss）等。

线性回归

给定一组数据 ${(\boldsymbol{x}_1, y_1), …, \boldsymbol{x}_n, y_n}$，用一个模型来估计最接近 $y_i$ 的连续标量。

考虑用一个线性函数来拟合。

$$
f(x_i) = \boldsymbol{w}^T \boldsymbol{x}_i + b
$$

这里可以通过在所有 $\boldsymbol{x}_i$ 后面加一个 $1$ 然后把 $b$ 整合进 $\boldsymbol{w}$ 中来消掉常数项。

采用 $L_2$ Loss 来衡量差异：

$$
\mathbb{E}((f(X) - Y)^2)
$$

将 $(\boldsymbol{x}_1, …, \boldsymbol{x}_n)$ 记为 $\mathbf{A}$，$(y_1, …, y_n)^T$ 记为 $\boldsymbol{y}$，那么根据线性代数经典结论，$\boldsymbol{w}$ 是

$$
\mathbf{A}^T\mathbf{A}\boldsymbol{x} = \mathbf{A^T}\boldsymbol{y}
$$

的解。该方程总是有解，且在 $\mathbf{A}^T\mathbf{A}$ 可逆时有 closed-form 解。

虽然如此我们不会用矩阵求逆来计算解，而是使用 Gradient Descent 法来求近似解。换言之从一个初始点开始，不断迭代：

$$
\boldsymbol{x}’ = \boldsymbol{x} + \alpha \nabla L(\boldsymbol{x})
$$

其中 $\alpha$ 为学习率，$L$ 为损失函数。如果 $\alpha$ 小，收敛慢，残差小；$\alpha$ 大，收敛快，残差大且可能振动。

如果数据量小于特征维度时 $\mathbf{A}^T\mathbf{A}$ 不可逆，没有 closed-form 解。此时要保证模型不会过拟合到这些数据，依然具有充分好的泛化性能，我们应当对模型进行正则化。

Hint. 正则化为什么是有道理的（正则化的本质）

这里本质上是数据不能给我们足量的信息，于是我们假设参数满足某个先验分布然后做 MAP。即（下面要学习的参数是 $\boldsymbol{\beta}$）

$$
\mathrm{argmax}_\theta \log p((\boldsymbol{x}_i, y_i) | \boldsymbol{\beta}, \theta^2) + \log p(\boldsymbol{\beta})
$$

假设 $\boldsymbol{\beta}$ 服从

$$
p(\boldsymbol{\beta}) \propto \exp(-\boldsymbol{\beta}^\boldsymbol{\beta} / \tau^2)
$$

此时先验分布一项变成了

$$
\lambda ||\boldsymbol{\beta}||^2
$$

即 $L_2$ loss 的某个倍数。

如果假设 $\boldsymbol{\beta}$ 服从 Laplace 分布即

$$
p(\boldsymbol{\beta}) = \exp(|\boldsymbol{\beta}| / \tau^2)
$$

那么就会产生

$$
\lambda ||\boldsymbol{\beta}||
$$

分别对应了 Ridge Regression 和 Lasso Regression 正则项。

从几何角度感性理解，Ridge Regression 生成每一维都较小的解，Lasso Regression 生成稀疏解。

逻辑回归

模型输出

$$
\hat{y} = f_{w, b}(\boldsymbol{x}) = \frac{1}{1 + \exp(-\boldsymbol{w}^t\boldsymbol{x} + b)}
$$

本质上是

$$
\ln \frac {\hat{y}} {1-\hat{y}} = \boldsymbol{w}^T\boldsymbol{x} + b
$$

相当于一个线性模型输出分类为正类的相对概率。这时如果 ground truth 为正类，$\hat y$ 就是给定数据，模型输出正类的概率，可以认为是得到某个参数的后验概率，ground truth 为负类时 $1 - \hat{y}$ 的意义同理。

此时假设正类为 $1$ 负类为 $0$，得到 MAP 的目标函数为

$$
y \ln f_{w, b}(\boldsymbol{x}) + (1-y) \ln (1 - f_{w, b}(\boldsymbol{x}))
$$

发现是真实分布和估计分布之间的交叉熵。

在优化的时候需要计算梯度。简单计算一下可以知道

$$
\frac{\partial L}{\partial w_i} = \sum_{j=1}^n -(y_j - f_{w, b}(\boldsymbol{x}^j))x^j_{i}
$$

不采用 $L_2$ Loss 而是采用 Cross Entropy Loss 的理由是 $L_2$ Loss 计算梯度可以得到

$$
\frac{\partial L_2}{\partial w_i} = 2(f_{w, b}(\boldsymbol{x}) - y)f_{w, b}(\boldsymbol{x})(1-f_{w, b}(\boldsymbol{x}))x_i
$$

当 $y = 0$ 时，预报接近目标和远离目标均发生梯度消失。

其他东西

• Multinomial Logestic Regression 用 Softmax 函数激活，多分类。
• NN Classifier 和 $k-$NN Classifier，超参数为 $k$ 和距离函数。

超参数的确定方法为进行 Cross Validation，在验证集上调参，选取平均结果最好的一组。

• $k-$means 聚类的一个未知近似比的算法：随机撒点，重复对数据点找最近的关键点，关键点 Recenter 到离其最近的数据点的 means。

关键点的选择对种子非常敏感，有些收敛很慢或者收敛到非最优解。选择是应当尽量让初始种子互相远离并且多次随机。

神经网络

• Bias：改变输出的范围。
• 激活函数：Sigmoid，Tanh（多用于限制范围回归），ReLU，Leaky ReLU，Softmax。为神经网络模型提供非线性性。
• 损失函数：交叉熵，$L_p$ 范数，MSE（均方误差，即 $L_2$），MAE（平均绝对误差，即 $L_1$）

为了做梯度下降，需要求解每一层的梯度。

假设 $f(\boldsymbol{x})$ 为激活函数，$\mathcal{L}$ 为损失函数。层数为 $L$。网络结构为

• 输出 $\mathcal{L} = (\boldsymbol{y} - \boldsymbol{a}^L)^2$
• 全连接 $\boldsymbol{z}^i = \mathbf{W}^{lT}\boldsymbol{a}^{l - 1} + \boldsymbol{b}^l$
• 激活 $\boldsymbol{a}^l = f(\boldsymbol{z}^l)$

为了递推我们记录中间结果，令

$$
\delta^l = \frac{\partial \mathcal{L}}{\partial \boldsymbol{z}^l}
$$

那么对于输出层

$$
\delta^L = \frac{\partial \mathcal{L}}{\partial \boldsymbol{a}^L} f’(\boldsymbol{z}^L)
$$

对于其他层

$$
\begin{align}
\delta^l &= \frac{\partial \mathcal{L}}{\partial \boldsymbol{z}^l} \\
&= \frac{\partial \mathcal{L}}{\partial \boldsymbol{z}^{l + 1}}\frac{\partial \boldsymbol{z}^{l + 1}}{\partial \boldsymbol{z}^l} \\
&= \delta^{l + 1}\frac{\partial}{\partial \boldsymbol{a}^l}((\mathbf{W}^{l+1})^T\boldsymbol{a}^l + \boldsymbol{b}^{l + 1})\frac{\partial \boldsymbol{a}^l}{\partial\boldsymbol{z}^l} \\
&= \delta^{l + 1} (\mathbf{W}^{l+1})^T f’(\boldsymbol{z}^l)
\end{align}
$$

通过辅助变量可以直接算出梯度

$$
\begin{align}
\frac{\partial \mathcal{L}}{\partial \mathbf{W}^l} &= \frac{\partial \mathcal{L}}{\partial \boldsymbol{z}^l}\frac{\partial \boldsymbol{z}^l}{\partial \mathbf{W}^l} && = \delta^l (\boldsymbol{a}^{l-1})^{T} \\
\frac{\partial \mathcal{L}}{\partial \boldsymbol{b}^l} &= \frac{\partial \mathcal{L}}{\partial \boldsymbol{z}^l}\frac{\partial \boldsymbol{z}^l}{\partial \boldsymbol{b}^l} && = \delta^l
\end{align}
$$

Remark. 这个推导看起来很神秘。事实上你如果严格把每一层都写开，它确实就是对的。这里我们简单解说一下上面和下面都是矩阵的求偏导，来让他看起来有道理一点。

$\dfrac{\partial \mathbf{A}}{\partial \mathbf{B}}$ 表示 $\dfrac{\partial}{\partial \mathbf{B}} \otimes \mathbf{A}$，这里 $\otimes$ 表示 Kronecker 积。其中 $\dfrac{\partial}{\partial \mathbf{B}}$ 是一个算子，它作用在一个元 $f$ 上得到的结果和 $\mathbf{}{B}^T$ 有相同的形状，其中

$$
\frac{\partial f}{\partial \mathbf{B}}_{ij} = \frac{\partial f}{\partial B_{ji}}
$$

你可以自行验证这个算子的线性性，和写成这种形式的求导线性性、链式法则均成立。

ReLU 函数 可以用来防止梯度消失，同时可以看到 ReLU 函数激活相当于将某一个点的斜率加上一个值（Slope Trick），因此可以用若干个并排的 ReLU 神经元来拟合复杂曲线。

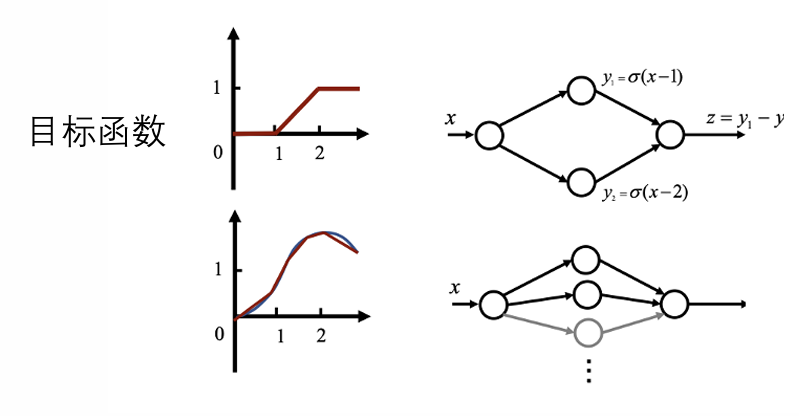
• 优化方法
  • 梯度下降
  • 随机梯度下降（SGD）
  • 自适应学习率的梯度下降（RMSProp, Adagrad, Adam, AMSGrad, AdaBound 等）
• 超参数调整
  • 在 Validation Set 上调整超参数
• 防止过拟合
  • 正则化
  • 数据增强
  • 提前停止
  • Dropout

CNN

批话

人眼识别有平移不变性，相当于空间上的权重共享。

• 卷积核（滤波器）形状包括

  • Padding（边框）
  • Strides（步长）
  • Filter size（矩阵大小）

  容易根据两块之间的大小差距计算上面三个东西、参数量、感受野大小。

• 空洞卷积 可以获得更大的感受野

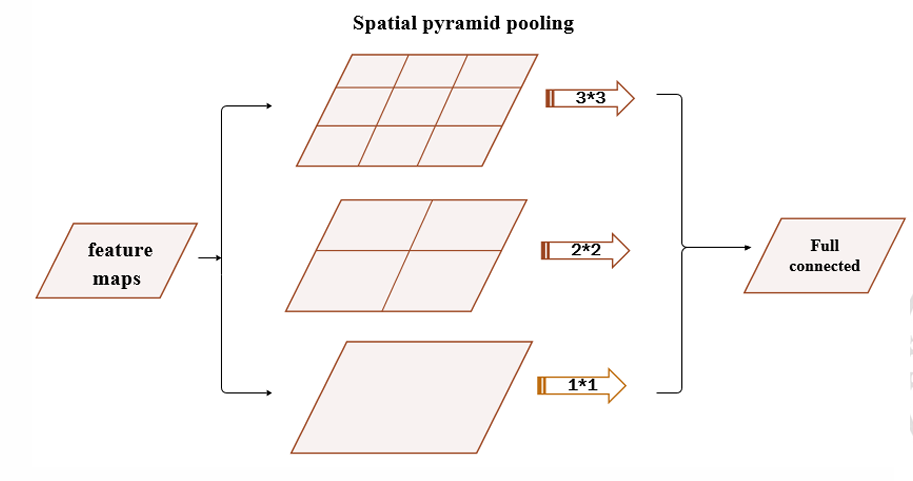
• 池化 MaxPooling，MeanPooling，空间金字塔池化。

  

• 分层表示学习 堆叠多个层次的卷积层来构建神经网络，目的是获得更大的感受野。越靠近输入的层看到的特征越细。

• 反卷积 实现 decode 的过程。

代表性网络

• AlexNet 创造历史，取得 $10%$ 的性能提升。
• VGG16 连续的 $3\times 3$ 卷积层等效于一个具有更大感受野的卷积层，参数量更小。可以作为 Feature Extractor。
• ResNet 加入残差连接（浅层特征和深层特征求和）。
• 三个快速网络

  • Squeeze Net，其中有一种 Fire Block 机制（将正常卷积和一个 $1\times 1$ 卷积块拼在一起），在 CPU 上非常快。

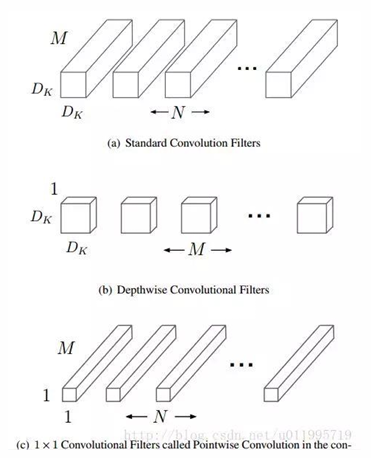
  • Mobile Net，采用深度可分离卷积的 Trick，先对每一个 input channel 做卷积，然后通过逐点卷积对得到的特征进行混合。观察下图可以发现参数量明显减少（$M$：input channels，$N$：output channels，$D_k$：特征图尺寸）。

    

  • Shuffle Net，组卷积，同组共享权重，然后打乱层，将不同组的信息合并。

应用

Object Detection

一种监督学习任务。

采用 Jacard Similarity（课件中叫做交并比，Intersection over Union）来判定是否检测成果。如果 Jacard Similarity 大于某个阈值，则认为检测成功。

评估模型一般考虑下面几个比例

真实值 \ 预测值	反例	正例
反例	TN（真阴性）	FP（假阳性）
正例	FN（假阴性）	TP（真阳性）

一般检查下面两个量

• 精度 $\mathrm{Precision} = \dfrac{\mathrm{TP}}{\mathrm{TP} + \mathrm{FP}}$。
• 召回 $\mathrm{Recall} = \dfrac{\mathrm{TP}}{\mathrm{TP} + \mathrm{FN}}$。

下面是代表性算法。

• R-CNN

  1. 选择性搜索算法，提取约 2000 个候选区域。我不知道选择性搜索算法是如何工作的。
  2. Resize 每个候选区域，喂给 VGG 生成特征图。
  3. 喂给 SVM Classifier。
  4. 非极大值抑制。

  有以下局限：

  • 选择性搜索速度慢。
  • Resize 候选区域影响分类准确性。
  • 每个区域单独输入 VGG 非常慢。
  • 非端到端。

• SPP Net

  先把整张图喂给 VGG 得到特征图，然后在特征图上用选择性搜索得到区域。

  对候选区域使用空间金字塔池化，然后喂给 SVM。

  解决了 R-CNN 的第二、第三个局限性。

• Fast R-CNN 将空间金字塔池化换成简化版的感兴趣区域池化（ROI），将 SVM 换成神经网络。

  实现了近似端到端训练。

• Faster R-CNN 将选择性搜索换成区域提议网络（Region Proposal Network）。

  速度更快，实现了真正的端到端训练。

• YOLO 删掉区域提议。首先将图划分成 $7\times 7$ 的网格，每个网格负责预测两个中心在其内部的 Bounding Box 和分类标签，以及匹配到每种物体的概率（注意可以有两个边界框，但只匹配一种物体），最后保留置信度高的边界框，并做非极大值抑制。

  只需要看一次图，但其局限性为难以检测小物体。

• YOLO v2 预定义先验框。

• Single Shot Multibox Detector（SSD） 另一种只看一次的算法。

Image Segmentation

细粒度的分类。使用全卷积神经网络。

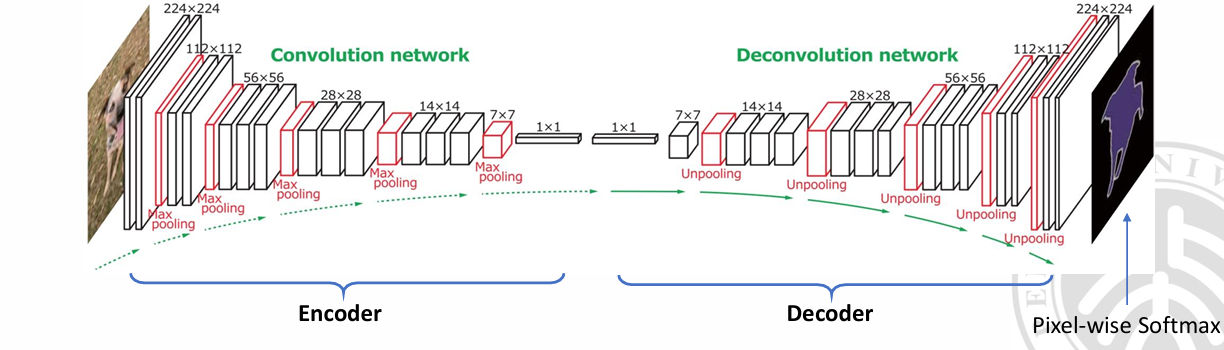
随着层数增加，低级别特征可能会丢失，因此考虑跳跃连接。

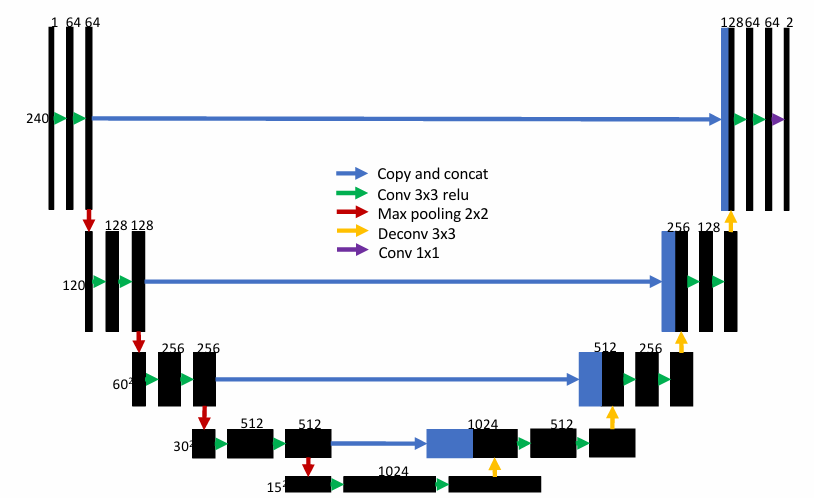
用了这个 trick 的两个网络：

• SegNet

  

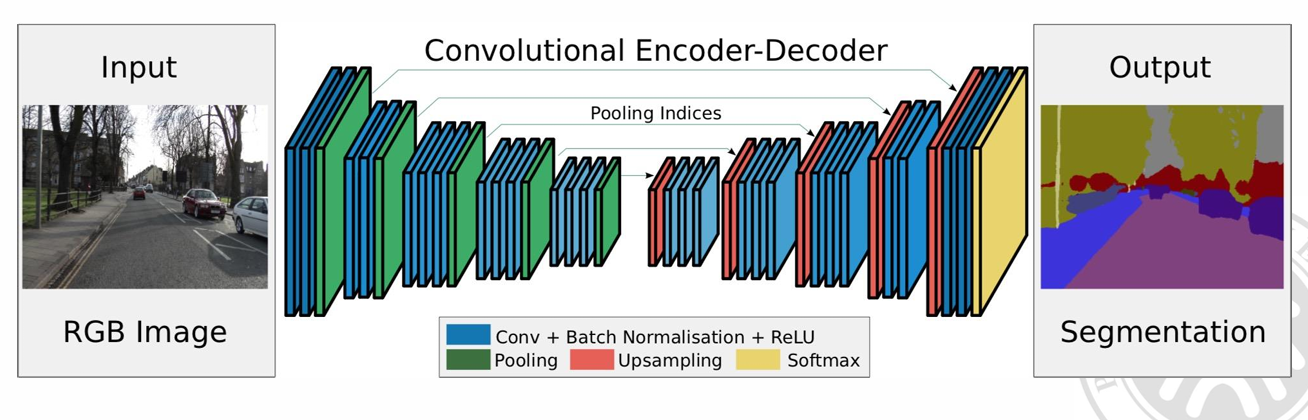
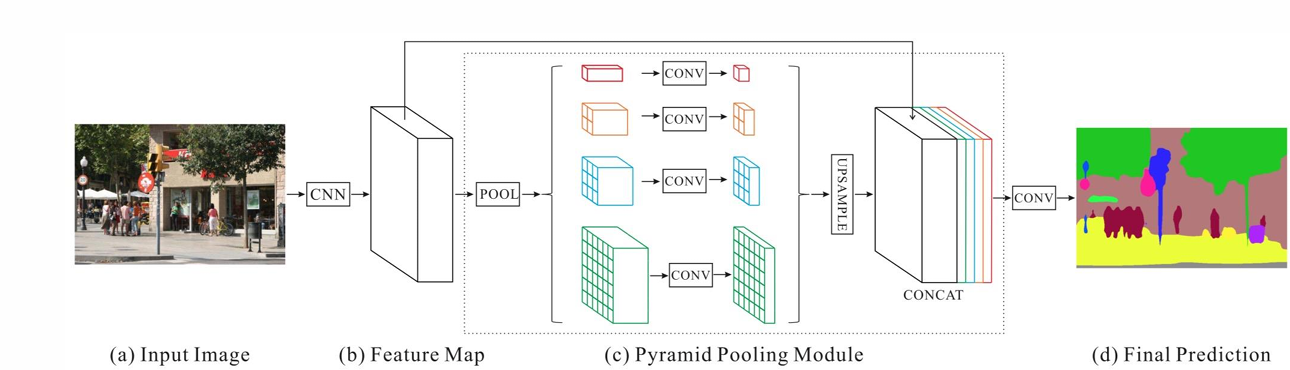
• PSPNet（Pyramid Scene Parsing Network）

  

衡量模型表现可以考虑：

• Pixel-wise cross entropy，对每个像素算交叉熵，对于分割小物体的性能较差。

• Dice coefficient，将预测区域看成 01 向量（按是否在内部）定义

  $$
  \mathrm{Dice} = \frac{2|A\cdot B|}{|A| + |B|}
  $$

  类似于 IoU，但是可以求导。

图像分割的一个更强的任务是 Instance Segmentation。

$$
\mathrm{Instance Segmentation} = \mathrm{Object Classification} + \mathrm{Object Detection} + \mathrm{Semantic Segmentation}
$$

代表算法是 Mask R-CNN。

Segmentation 的时候容易丢失小物体和边界信息，因此有如下技巧：

• 镜像填充。
• 损失加权，增加边缘权重、小物体权重。

Face Recognition

1. 检测图像中的人脸位置。
2. 将人脸对齐到图像中心。
3. 身份识别。

可以进行分类

• Identification（识别出来是谁）
• Verification（判断是不是给定人）

按照是否动态分为

• Close-set，人脸数据不会变化，简单的分类问题。
• Open-set，会输入新的数据，注意你不能重新训练模型。

Open-set 的问题是特征提取问题。本质上是通过监督学习来学习区分特征空间。要点是设计新的网络架构和损失函数。

---

其他一些应用：

• Pose Estimation
  • Convolutional Pose Machine, CPM Top-down 算法。先找人的边界框，然后提取特征，再用 CNN 输出关键点的 heatmap。
  • OpenPose，CPM + Bottom-up。在 CPM 的基础上输出肢节的 heatmap。
  • Pose Proposal Networks, PPN，YOLO + OpenPose（视为目标检测问题）。

GAN

判别式模型寻找决策边界，生成式模型寻找联合分布。

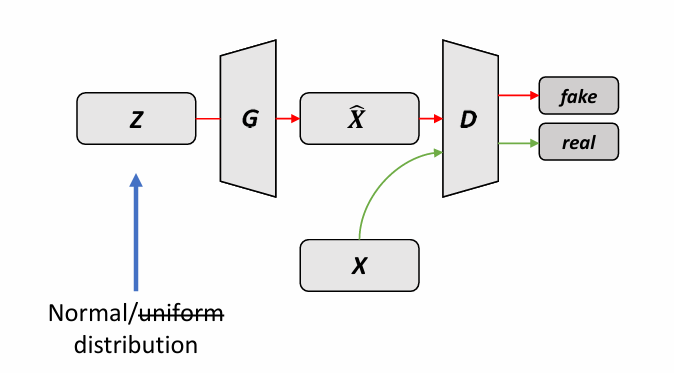
其中 $G$ 相当于构造一个从 Gauss 向量到另一个向量的一一映射。$G$ 的目标是生成像是数据集中的图像，$D$ 的目标是区分图像是否来自数据集。

分开来看，两个网络的损失函数分别是

$$
\begin{align}
\mathcal{L}_D &= -\mathbb{E}_{\boldsymbol{x} \sim p{data}} \log D(\boldsymbol{x}) - \mathbb{E}_{\boldsymbol{z}\sim p_z}\log(1 - D(G(\boldsymbol{z}))) \\
\mathcal{L}_G &= -\mathbb{E}_{\boldsymbol{z}\sim p_z}\log D(G(\boldsymbol{z}))
\end{align}
$$

感性理解，我们可以直接优化

$$
\min_G\max_D V(D, G) = \mathbb{E}_{\boldsymbol{x} \sim p_{data}} \log D(\boldsymbol{x}) + \mathbb{E}_{\boldsymbol{z}\sim p_z}\log(1 - D(G(\boldsymbol{z})))
$$

注意后一项的增减性。定义 $p_g$ 为 $\boldsymbol{z}\sim p_z$ 时 $G(\boldsymbol{z})$ 的概率分布。那么损失函数变成

$$
\min_G\max_D V(D, G) = \mathbb{E}_{\boldsymbol{x} \sim p_{data}} \log D(\boldsymbol{x}) + \mathbb{E}_{\boldsymbol{z}\sim p_g}\log(1 - D(\boldsymbol{z}))
$$

Claim. 该损失函数达到全局最优解时 $p_g = p_{data}$。

Proof.

考虑 $G$ 固定，那么

$$
V(G, D) = \int_{\boldsymbol{x}} p_{data}\log D(x) + p_g(\boldsymbol{x})\log(1 - D(\boldsymbol{x}))\mathrm{d}x
$$

现在 $D$ 想要最大化这个函数，需要放出被积函数的一个下界，根据费马原理达到下界时必然有（注意这里把 $D(\boldsymbol{x})$ 看成变量）

$$
\frac{\partial}{\partial D(\boldsymbol{x})}p_{data}\log D(x) + p_g(\boldsymbol{x})\log(1 - D(\boldsymbol{x})) = \frac{p_{data(\boldsymbol{x})}}{D(\boldsymbol{x})} - \frac{p_g(\boldsymbol{x})}{1 - D(\boldsymbol{x})}
$$

注意此时 $D$ 时全局最优解，因此最优的 $D^*$ 满足

$$
D^* = \frac{p_{data}}{p_g + p_{data}}
$$

接下来固定 $D^*$，$G$ 想要最小化

$$
\mathbb{E}_{\boldsymbol{x}\sim p_{data}} \log \frac{p_{data}(\boldsymbol{x})}{p_{data}(\boldsymbol{x}) + p_g(\boldsymbol{x})} + \mathbb{E}_{\boldsymbol{x}\sim p_g}\log \frac{p_g(\boldsymbol{x})}{p_{data}(\boldsymbol{x}) + p_g(\boldsymbol{x})}
$$

这个式子和两个 KL 散度的和只差一个常数（分母必须是一个分数），我们通过减去 $2\log 2$ 来进行微调，原式等于

$$
-2\log 2 + D_{KL}(p_{data} || \frac{p_d + p_{data}}{2}) + D_{KL}(p_{g} || \frac{p_d + p_{data}}{2})
$$

根据 Gibbs 不等式取下界当且仅当 $p_g = p_{data} = \frac{p_d + p_{data}}{2}$，解得此时 $p_g = p_{data}$

训练时应当分多步反复训练 $G$ 和 $D$ 而不是一开始就将 $D$ 训练至最优：给 $G$ 一个优化的动力。

经典算法

• DCGAN 使用卷积神经网络。使用的 technique 如下
  • 对所有层批量归一化，除了 $G$ 的最后一层和 $D$ 的输入层，衰减系数 $0.9$。
  • 使用 Adam，一阶动量 $0.5$。
  • $0.2\alpha$ 的 Leaky ReLU。
  • 跨步卷积替代最大池化。
  • 学习率 $0.0001$。

在 DCGAN 之前使用 VAE 做生成式任务（训练一个 Encoder 从 data 打到高斯分布，然后训练一个 Decoder，计算 $L_2(\boldsymbol{x}, D(E(\boldsymbol{x})))$）。VAE 可以学习 Latent Representation（Noise vector 的线性组合具有语义性）

采用 MSE 的 VAE 不能重构小物体，但是用对抗损失和 MSE 结合可以重构小物体，因为小物体遵循可预测的模式。

• Conditional GAN 多一个分类标签。损失函数上面加上和 $c$ 有关系的信息。

  套上 RNN 可以做文生图。

  

---

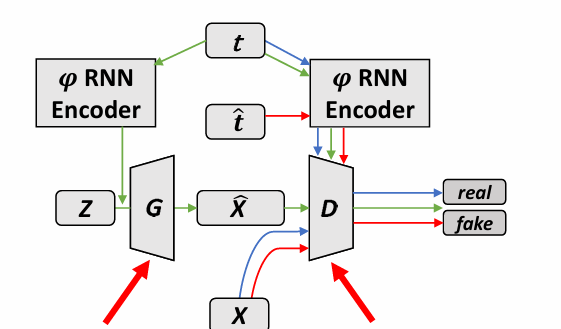
现在希望 GAN 也可以学习 Latent Representation。

采用暴力的方法，直接训练 Encoder

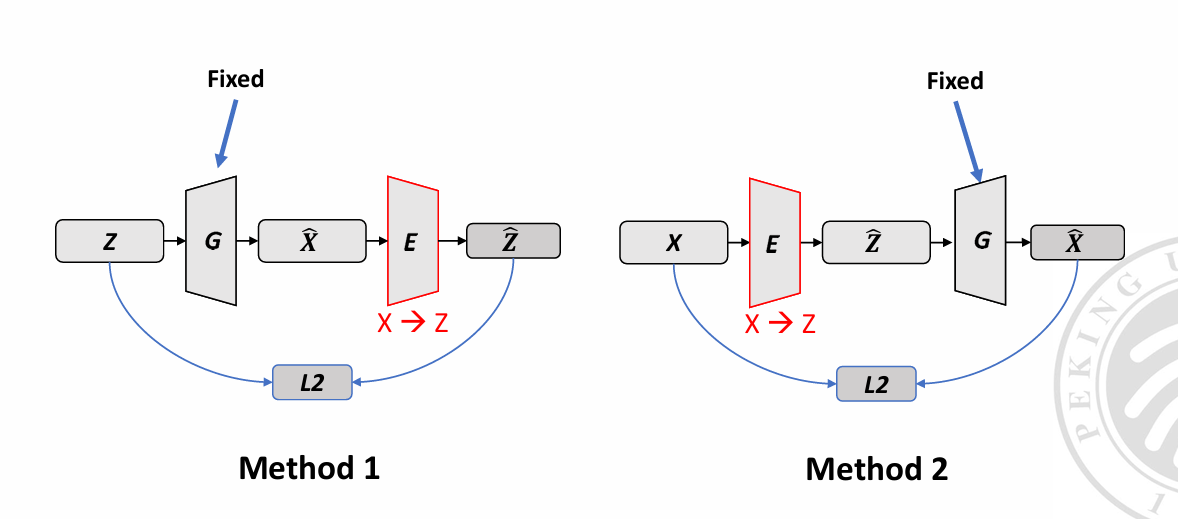
效果都不好（前者没有见过真图，G 不能生成所有图片；后者 G 不一定能生成给定的图片）。

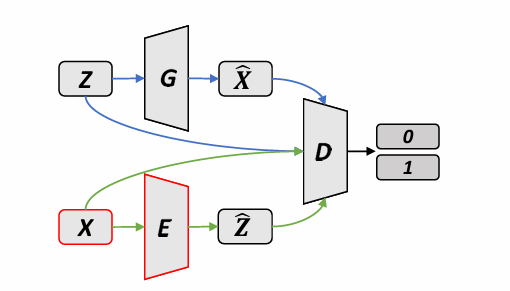
• BiGAN D 的读入是一张图及其 Latent Representation。

  

• CoGAN 寻找两个领域的联合分布（希望能做图像翻译）

  

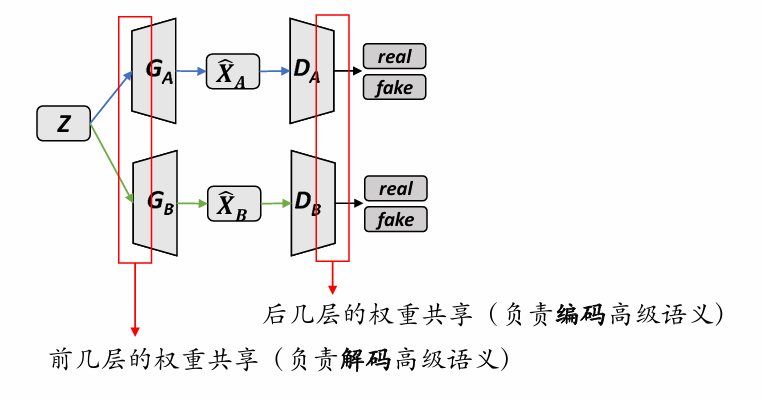
  但是这个给定一个领域的图片不能生成另一个领域的图片，还需要训练一个 Encoder 打回 Latent Represectation。

• Cycle GAN 解决上面的问题。

  

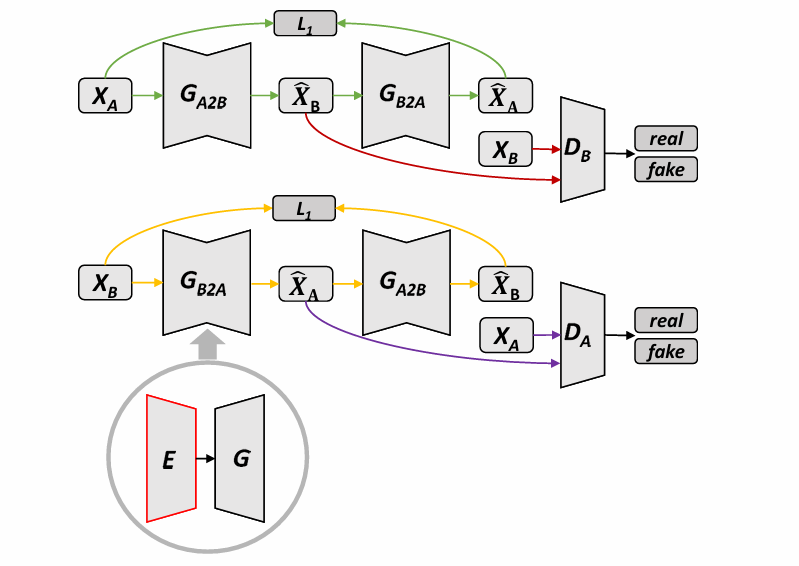
  希望如果在 $G_B$ 中输入了 $A$ 还是得到 $A$，故引入 Identity loss：

  $$
  L_2(X_A, G_A(E_B(X_A)))
  $$

RNN

时间序列分析用模型。

首先考虑词的表示。

• Onehot。维数灾难，过于稀疏。

• Bag of Words。维数灾难，丢失位置信息。

• Word Embedding。要求包含语义信息，相似单词有相似表示，算术运算和语义操作同构。

  自监督学习（通过比较上下文来找嵌入模式）。

  • Word2Vec：CBOW/Skip-Gram + 负采样

    连续词袋模型（CBOW），根据上下文窗口预测中间词。

    Skip-Gram 给定中间词，最大化上下文的概率。这里因为输出的是上下文的词出现的概率，所以用 Sigmoid 而不是 Softmax。当词汇表大的时候计算量很大，因此考虑直接采样近似。

---

接下来给出朴素 RNN 的结构。

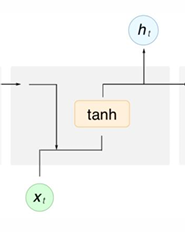
其中 $h_t$ 表示当前时间步的某种信息，$y_t$ 表示当前步的输出，$\sigma$ 是某个激活函数。

$$
\begin{align}
h_t &= \tanh(W_hx_t + U_hh_{t - 1} + b_h) \\
y_t &= \sigma(W_yh_t + b_y)
\end{align}
$$

难以解决长期记忆问题，因此提出 LSTM（长短期记忆网络）。

首先定义门函数（Gate Function），是一个诸维度都在 $[0, 1]$ 的向量，用于控制记忆、遗忘某些维度的信息。

额外定义 $c_t$ 表示时间 $t$ 时的 Cell Vector，用来从前往后传递信息。

将 $h_{t-1}$ 和 $x_t$ concat 起来，通过三个线性变换算出三个门（Sigmoid 激活）。LSTM 的循环单元如图

• 可以用 ReLU 替换 Sigmoid 函数。

---

考虑几个经典任务。

• Many-to-one 情感分类等。
• One-to-many 图片描述等。每一个时间步的输出作为下一个时间步的输入。用所有输出来计算损失（如平均交叉熵等）。
• 同步 Many-to-many 交通计数等。要保证每张图都对，所以说需要预先定义序列长度来计算损失。以及文本生成。
• 异步 Many-to-many Chatbot。

Transformer

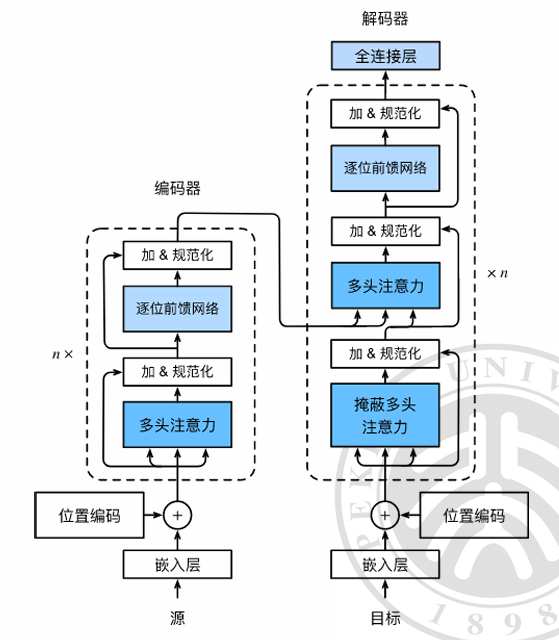
网络结构

• 非自主性提示 Key，Value
• 自主性提示 Query

自注意力机制

$$
\mathrm{Attention}(Q, K, V) = \mathrm{softmax}\left(\frac{K^TQ}{\sqrt {D_k}}\right) V
$$

softmax 以及里面包的东西成为注意力权重矩阵，因为 $K^TQ_{ij}$ 实际上是 $\langle K_i, Q_j\rangle$ 所以确实是某种相似度的计算。除掉 $\sqrt {D_k}$ 是为了防止点积过大，梯度过小。

多头注意力：将多个 self-attention 的结果 concat 起来。

位置编码

$$
\begin{align}
\mathrm{PE}(pos, 2i) &= \sin\left(\frac{pos}{10000^{2i / d_{\mathrm{model}}}}\right) \\
\mathrm{PE}(pos, 2i + 1) &= \cos\left(\frac{pos}{10000^{2i / d_{\mathrm{model}}}}\right)
\end{align}
$$

输入等于词向量 + 位置编码。

残差连接 将输入线性变换，使得其和注意力输出维度匹配，然后将两者相加，并且做 Layer Normalization。

逐位前馈网络 两个全连接层，第一个之后用 ReLU 激活。

多编码器堆叠 将多个编码器串联起来，得到最终输出。

掩蔽多头注意力 在 $K^TQ$ 上面加上 attention mask 矩阵，该矩阵形如

$$
\begin{pmatrix}
0 & -\infty & \cdots & -\infty & -\infty \\
0 & 0 & \cdots & -\infty & -\infty \\
\vdots & \vdots & & \vdots & \vdots \\
0 & 0 & \cdots & 0 & -\infty \\
0 & 0 & \cdots & 0 & 0 \\
\end{pmatrix}
$$

该矩阵屏蔽了后面的信息（生成文本时不需要考虑下文）。

掩蔽多头注意力的输出作为 $Q$，和编码器输出作为 $K, V$ 再过一个多头注意力。

预训练模型

在无标签数据上学习通用语言表示，从而提高 NLP 任务的性能。

1. 预训练阶段 再大量无标签文本数据上预训练。
2. 微调阶段 针对特定任务进行微调。

• GPT 学习单向上下文信息。

  使用 Transformer 的 Decoder 堆叠。无监督学习，最大化对下一个词的预测概率。

  微调阶段D为特定任务添加相关的头部（分类层、标注层）。

  

• BERT 学习双向上下文信息。

  使用 Transformer 的 Encoder 堆叠。有两个任务：

  • MLM（Masked Language Modeling） 将一些词替换为 <SEP>，做完形填空。
  • NSP（Next Sentence Prediction）输入两个连续的句子，判断是否为连续上下文。用 Segment Embedding 来使模型可以区分多个句子。

大模型参数规模提升带来了能力涌现。（模型基本结构和训练方式基本不变，只增大模型和数据规模）原因为

• 大量的训练数据：人类积累的所有信息
• 模型容量：充分学习数据
• 自回归和无监督训练：不需要标注海量数据
• 迁移学习和微调：适应不同任务
• 多任务学习：提高泛化性