Information and Entropy (7) Processes
Abstract. 在上一节的基础上继续讨论一些通信过程的性质。
我们讨论的处理过程具有如下特点:
- Discrete. 输入是一组互斥事件集,每时每刻只会有一个发生,输出是另一个互斥事件集。
- Finite. 上述两个事件集均为有限集。
- Memoryless. 当前输出只取决于当前输入,和之前的输入没有关系。
- Nondeterministic. 对于相同的输入可能输出不同的结果(“噪声”)。
- Lossy. 从输出中无法反推输入。
大概是总结了之前的 Communication System 的特点。
下面几节感觉很平凡,均为常识内容,我们直接跳到第三节。
Information, Loss and Noise
和上一节相同,我们定义输入的信息量为
$$
I = \sum p(A_i)\log\left(\frac 1{p(A_i)}\right)
$$
输出的信息量为
$$
J = \sum p(B_i)\log\left(\frac 1{p(B_i)}\right)
$$
然后上一节还记述了对输入的不确定度的期望
$$
L = \sum_{j}\sum_{i} p(A_i, B_j) \log\left(\frac 1{p(A_i | B_j)}\right)
$$
这个值称为 loss,相应的,对输出的不确定度
$$
N = \sum_{j}\sum_{i} p(A_i, B_j) \log\left(\frac 1{p(B_j | A_i)}\right)
$$
称为 noise。
假设 $W$ 是输出端可以识别到输入端变化的最大速率,那么
$$
C = WM_{max}
$$
称为这个过程的 capacity。
上一节我们已经推导过了
$$
M = I - L = J - N
$$
因此有
$$
J = I - L + N
$$
或者简明地用下面的这个图来表示这个 discrete memoryless process 中的信息流动
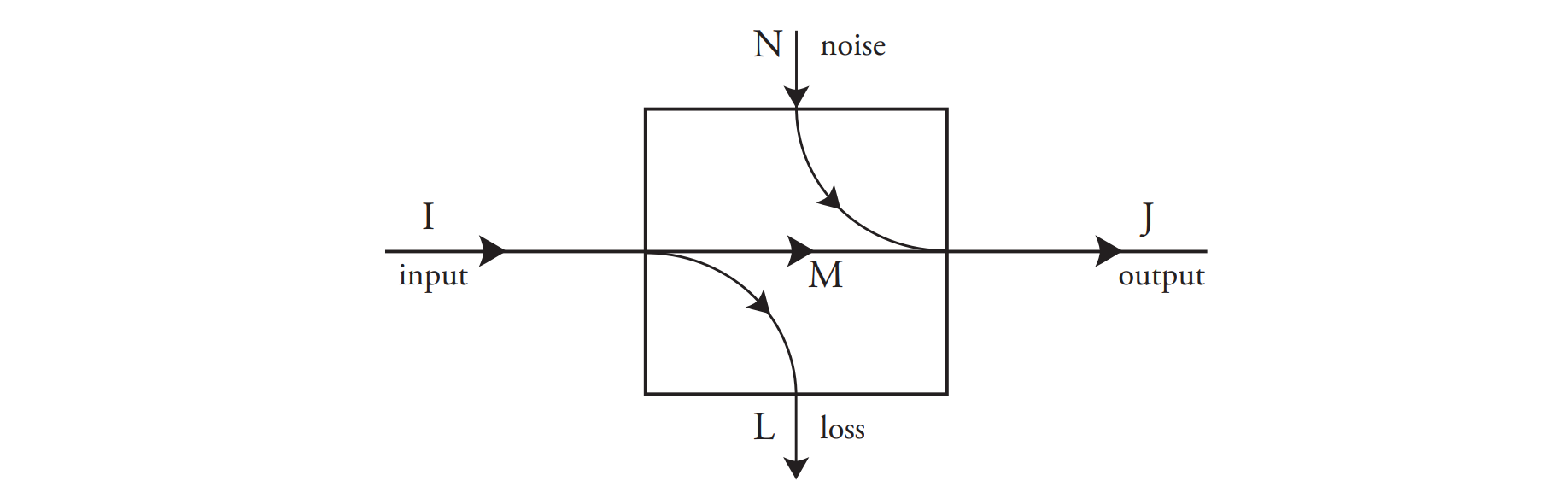
原论文中的记号 在 Shannon 的原论文中记号和这里不太一样,简单记录一下:
- 输入的概率分布称为 $x$,输出的概率分布称为 $y$。
- $H(x)\leftarrow I, H(y)\leftarrow J, H_y(x)\leftarrow L, H_x(y)\leftarrow N, R \leftarrow M$。
Example. 回忆我们在第 4 节中提到的 Hamming Code,在推导纠错码长度下界的过程中我们利用码距得到了
$$
2^n \times m \leq 2^m
$$
接下来我们从信息熵的角度推导这个下界。
要求总是能够检查错误,也就是 $L = 0$,即
$$
I + N = J
$$
这里的输入信息量只能是原来的 $01$ 串的信息量,即 $n$,而 noise 只可能是反转 $m$ 个位置之一,也就是噪声的熵为 $N = \log_2 m$。输出是一个长度为 $m$ 的串,但是信息熵未必是 $m$,因为显然这里 $2^m$ 种情况不是都能取到的。
于是有
$$
I + N = n + \log_2 m = J \leq m \Rightarrow n + \log_2 m \leq m
$$
即上述不等式取对数的形式。
可能这个项目就到这里为止了。后面全是统计力学,量子力学之类的东西,不想看了。