Revision | 高等数学 A I(期末)
Abstract. 高等数学复习笔记,参考资料是李忠, 周建莹. 高等数学(上)。
微分中值定理
约定 共有三个,以下函数均在 $[a, b]$ 连续,在 $(a, b)$ 可导,出现在分母时均默认非零。
定理 1.(Rolle) 若 $f(a)=f(b)$
$$
\exists \xi \in (a, b). f’(\xi) = 0
$$
定理 2.(Lagrange)
$$
\exists \xi \in (a, b). f’(\xi) = \frac{f(a) - f(b)}{a - b}
$$
定理 3.(Cauchy)
$$
\exists \xi \in (a, b). \frac{f’(\xi)}{g’(\xi)} = \frac{f(a)-f(b)}{g(a) - g(b)}
$$
其中 Rolle 定理是三个定理的基础。Lagrange 定理是最常用的形式。Cauchy 定理应用似乎只有用于证明洛必达法则和泰勒公式。
Proof Sketch 1. 根据最大最小值定理和费马定理,只需证明存在非端点的极值点。若端点同时是最大值和最小值那么函数是常函数,否则最大值或者最小值不在端点。
Proof Sketch 2. 构造函数,给 $f$ 减去一条直线即可,再用罗尔定理
Proof Sketch 3. 构造函数再用罗尔定理。
$$
H(x) = (f(x) - f(a))(g(b) - g(a)) - (f(a) - f(b))(g(x) - g(a))
$$
Lagrange 定理可以导出如下重要命题,此命题是不定积分加常数的依据。
命题 4. $f’(x) \equiv 0 \Leftrightarrow f(x) \equiv f(a)$。
Proof.
根据 Lagrange 定理,对于任意 $x\in (a, b]$ 都有
$$
\exists \xi. f(x) = f(a) + (x - a) f’(\xi)
$$
而 $f’(\xi)\equiv 0$,因此 $f(x) \equiv f(a)$。$\square$
事实上在实际问题当中我们经常是构造函数然后使用罗尔定理,但是构造函数的方法不一定很明显。像上面拉格朗日中值定理的 Proof Sketch 中的借助几何直观的构造不一定能够完成。因此我们给出一个比较去智慧化的证明。
Proof.
现要证明
$$
\exists \xi. f’(\xi) - \frac{f(b) - f(a)}{b - a} = 0
$$
根据罗尔定理我们只需要证明如下函数有两个零点。
$$
f(x) - \frac{f(b) - f(a)}{b - a}x + C
$$
根据 $\xi$ 可能的范围和出于这两个零点应当尽可能平凡的猜测,这个零点应当就是 $a, b$。代入之后可以得到关于 $C$ 的方程,事实上你可以发现他们确实也是同解的。
当然罗尔定理有如下广义形式。
定理 1-1. 若 $f(x)$ 在 $\mathbb{R}$ 上可导且 $\lim\limits_{x\rightarrow \infty} f(x) = l$,那么存在 $\xi$,$f’(\xi) = 0$。
一种证明方法是寻找 $f(a) = f(b)$ 的点,然后做一些讨论,比较初等,下面我们给出一个比较阴间的证明。
Proof.
考虑构造函数
$$
F(x) = \begin{cases}
f(\tan x), & -\frac \pi 2 < x < \frac \pi 2 \\
l & x = \pm \frac \pi 2
\end{cases}
$$
可以证明 $F(x)$ 满足罗尔定理的条件,于是存在 $-\frac \pi 2 < \xi < \frac \pi 2$ 使得 $F’(\xi) = 0$。
$$
F’(\xi) = \frac{f’(\xi)}{\cos^2 \xi} \Rightarrow f’(\xi) = 0
$$
$\square$
洛必达法则
定理 5.(L’Hospital) 设函数 $f(x), g(x)$ 在某点 $x_0$ 的邻域内可导,且 $f(x_0) = g(x_0) = 0$,若 $\lim\limits_{x\rightarrow x_0}\dfrac{f’(x)}{g’(x)}$ 存在,$\lim\limits_{x\rightarrow x_0}\dfrac{f’(x)}{g’(x)}$ 也存在,且这两个极限相等。
只需要在分子分母上同时配一个 $-0$ i.e. $-f(x)$ 和 $-g(x)$,然后用 Cauchy 中值定理即可。
这是 $\frac 00$ 型未定式上的洛必达法则,此外还有 $\frac \infty \infty$ 型未定式上的洛必达法则,证明难度是 $\frac 00$ 上的形式的完全上位。
定理 6.(L’Hospital) 设函数 $f(x), g(x)$ 在某点 $x_0$ 的邻域内可导,且 $\lim\limits_{x\rightarrow x_0}f(x) = \lim\limits_{x\rightarrow x_0} g(x) = \infty$,若 $\lim\limits_{x\rightarrow x_0}\dfrac{f’(x)}{g’(x)}$ 存在,$\lim\limits_{x\rightarrow x_0}\dfrac{f’(x)}{g’(x)}$ 也存在,且这两个极限相等。
Proof.
设 $\lim\limits_{x\rightarrow x_0}\dfrac{f’(x)}{g’(x)} = A$,我们要证明
$$
\lim_{x\rightarrow x_0}\left|\frac{f(x)}{g(x)} - A\right| = 0
$$
对于一个 $x_1 > x$,进行一些放缩
$$
\begin{aligned}
&\left|\frac{f(x)}{g(x)} - A\right| \\
=&\left|\frac{f(x) - f(x_1)}{g(x)} - A + \frac{f(x_1)}{g(x)}\right| \\
\leq&\left|\frac{f(x) - f(x_1)}{g(x)} - A\right| + \left|\frac{f(x_1)}{g(x)}\right| \\
\leq& \left|\frac{g(x)}{g(x) - g(x_1)}\right|{\color{blue}\left|\frac{f(x) - f(x_1)}{g(x) - g(x_1)} - A\right|} + |A|\left|\frac{g(x_1)}{g(x)}\right| + \left|\frac{f(x_1)}{g(x)}\right|
\end{aligned}
$$
对蓝色的部分用中值定理,变成
$$
\leq \left|\frac{g(x)}{g(x) - g(x_1)}\right|{\color{blue}\left|\frac{f’(\xi)}{g’(\xi)} - A\right|} + |A|\left|\frac{g(x_1)}{g(x)}\right| + \left|\frac{f(x_1)}{g(x)}\right|
$$
现在式子中第一项是有界乘无穷小,后面两项是无穷小。但是变量有两个,不是很直观,需要用 $\varepsilon-\delta$ 语言详细讨论一下,简便起见下面只写右极限,左边对称。
$\forall \varepsilon > 0$,我们有
$$
\lim_{x\rightarrow x_0} \frac{f(x)}{g(x)} = A \Rightarrow \exists \delta > 0. \forall x_0 < x < x_0 + \delta, \left|\frac{f’(x)}{g’(x)} - A\right| \leq \frac {\varepsilon} 4
$$
取 $x_1 = \frac{x_0 + \delta}{2}$,由于 $f(x), g(x)\rightarrow \infty$
$$
\begin{aligned}
\exists \delta_1. \forall x_0 < x < \min(x_1, x_0 + \delta_1). \qquad
& \left|\frac{g(x)}{g(x) - g(x_1)}\right| < \frac 43 \\
\wedge\quad & |A|\left|\frac{g(x_1)}{g(x)}\right| < \frac \varepsilon 3 \\
\wedge\quad & \left|\frac{f(x_1)}{g(x)}\right| < \frac \varepsilon 3
\end{aligned}
$$
因此当 $x_0 < x < x_0 + \delta_1$ 时
$$
\left|\frac{f(x)}{g(x)} - A\right| < \varepsilon
$$
因此原极限确实是 $A$。$\square$
Hint. 使用加一项减一项,然后用绝对值三角不等式放缩。
其余的情况也就是 $x\rightarrow \infty$ 的只需要构造 $F(x) = f(\frac 1x)$,然后补全可去间断点就可以规约到上面两个已经证明的情况。
Darboux 定理
Darboux 定理是导函数的中值定理。
定理 7.(Darboux) $f(x)\in D[x, y]$,对于任意介于 $f’(a)$ 和 $f’(b)$ 之间的 $\eta$,都存在一个 $\xi$ 使得 $f’(\xi) = \eta$。
Proof.
只需要证明 $\eta = 0$ 的情况,其他情况可以加一个一次函数来变化到此情况。
不妨设 $f’(a) < 0 < f’(b)$,其他情况对称。根据费马定理只需要证明存在一个非端点的极小值。
根据导数定义,这两个确实都不是极小值。$\square$
杂题
Problem 1 求
$$
\lim_{n\rightarrow \infty} n(\arctan(\ln(n + 1)) - \arctan(\ln(n)))
$$
Solution.
对括号里面的东西用拉格朗日中值定理,得到原极限其实等于
$$
\lim_{n\rightarrow \infty} n\ln\left(\frac{n + 1}{n}\right)\frac{1}{1+\xi^2}\\
\quad\text{where}\quad \xi \in (\ln(n), \ln(n + 1))
$$
前面是 $\mathrm{e}$ 的定义,后面是一个无穷小,因此原极限等于 $0$。
Problem 2 f(x) 在 $[a, b]$ 二阶可导, $f(a) = f(b) = 0$。
证明 $\forall x\in (a, b). \exists \xi \in (a, b). f(x) = \frac 12 f’’(\xi)(x-a)(x-b)$
Solution.
即证明
$$
\exists \xi. f’’(\xi) - \frac{2f(x)}{(x - a)(x - b)} = 0
$$
注意这里的 $x$ 是一个定值而非变量。构造一个函数
$$
g(t) = f’(t) - \frac{2f(x)}{(x - a)(x - b)}t + C
$$
现在要证明 $g’(t)$ 可以取到 $0$,只需要证明 $g(t)$ 在两处相等即可。通过取恰当的 $C$,变为 $g(x)$ 有两个零点。构造一个函数
$$
h(t) = f(t) - \frac{f(x)}{(x - a)(x - b)}t^2 + Ct + D
$$
只需要给出恰当的 $C, D$ 使得 $h(t)$ 有三个零点。我们构造
$$
H(t) = f(t) - \frac{f(x)(t - a)(t - b)}{(x - a)(x - b)}
$$
$H(t)$ 有三个零点 $a, x, b$,且符合上述形式。因此原结论成立。$\square$
Remark. 其实最后这一步有一点智慧了。如果想不到,可以考虑上面我们给出的拉格朗日中值定理的去智慧化的证明,用待定系数法把 $C, D$ 都解出来。很明显这里你需要猜测三个零点分别是 $a, b, t$。
Problem 3 $f(x)$ 在 $x = a$ 处有二阶导。证明
$$
\lim_{h\rightarrow 0} \frac{f(x+h) + f(x - h) - 2f(h)}{h^2}
$$
Solution.
展开至二阶小量,带 Peano 余项。
Remark. 这里二阶导不一定连续,所以说最后肯定是带 Peano 余项而不是 Lagrange 余项。
Problem 4. $f(x)$ 在 $a$ 附近二阶导连续且非零,由拉格朗日中值定理,存在函数 $\theta(h)\in(0, 1)$ 使得 $\forall h.$
$$
f(a + h) - f(a) = hf’(x + h\theta(h))
$$
证明 $\lim\limits_{h\rightarrow 0} \theta(h) = \frac 12$
Hint.
考虑用什么办法可以把 $f’(x + h\theta(h))$ 里面的 $\theta(h)$ 捞出来?
Solution.
两边都展开至二阶小量,带 Lagrange 余项。
$$
hf’(a) + \frac 12 h^2 f’’(a + \xi_1(h)) = hf’(a) + h^2\theta(h)f’’(a + \xi_2(h))
$$
化简一下得到
$$
\theta(h) = \frac 12 \frac{f’’(a + \xi_1(h))}{f’’(a + \xi_2(h))}
$$
两边取 $\lim$,根据连续性即得到原结论。$\square$
Problem 5-1. $f(x)$ 在 $\mathbb{R}$ 上有 $n$ 阶导数,且 $|f(x)|\leq A, |f^{(n)}(x)|\leq B$,求证 $f^{(i)}(x)$ 有界。
Solution.
对于任意的 $x$,我们将 $f(x + 1), f(x + 2), …, f(x + n)$ 在 $x$ 处泰勒展开,带拉个朗日余项。
$$
f(x + i) = f(x) + if’(x + i) + \cdots + \frac{i^n}{n!}f^{(n)}(x)
$$
将已知有界的部分全部摆在右边,就得到了 $n - 1$ 个关于 $f(x)$ $1\sim n - 1$ 阶导数的线性方程组。其系数矩阵为 $1, …, n$ 生成的范德蒙德行列式,记为 $V$。
那么有
$$
\begin{pmatrix}
f’(x) \\
f’’(x) \\
\vdots \\
f^{(n)}(x)
\end{pmatrix} = V^{-1}b
$$
其中 $b$ 的每一维都有界,于是 $f^{(i)}(x)$ 也都有界。$\square$
Problem 5-2. 具体地,当 $n = 2$ 时,可以证明 $\sqrt{AB}$ 是一个比较好的上界。
Solution(Sketch).
取 $f\left(x + \sqrt{\dfrac AB}\right)$ 在 $x$ 处的泰勒展开。
Problem 5-3. 关于有界性我们还可以进行一些讨论。
如果 $f(x)$ 在 $(a, b)$ 可导,但无界。可以证明 $f’(x)$ 也无界。
Proof Sketch. 取一个点,将其他点在此点处泰勒展开,带拉格朗日余项。
但是逆命题不一定成立。可以找到反例:
Example.
$$
f(x) = \sqrt x, x\in(0, 1)
$$
显然导函数无界,但是该函数有界。
Problem 6 求证若 $\lim\limits_{x\rightarrow +\infty} f’(x) = 0$,则 $\lim\limits_{x\rightarrow \infty} \dfrac{f(x)}{x} = 0$。
Solution.
用 $\varepsilon-\delta$ 语言验证。对于任意的 $\varepsilon > 0$,我们有
$$
\lim_{x\rightarrow +\infty} f’(x) = 0 \Rightarrow \exists \delta_0. \forall x > \delta_0, |f’(x)| < \frac \varepsilon 2
$$
取一 $x_0 > \delta_0$,对于 $x > x_0$
$$
\begin{aligned}
&\left|\frac{f(x)}x\right| \\
< &\left|\frac{f(x) - f(x_0)}{x - x_0}\right| + \left|\frac{f(x_0)}{x - x_0}\right|
= &\left|f’(\xi)\right| + \left|\frac{f(x_0)}{x - x_0}\right|
\end{aligned}
$$
其中 $\xi\in (x_0, x)$,$f’(\xi) < \frac \varepsilon 2$。而显然存在 $\delta$ 使得 $\left|\dfrac{f(x_0)}{x - x_0}\right| < \frac{\varepsilon}{2}$,因此 $x > \max(\delta, \delta_0)$ 时 $\left|\dfrac{f(x)}x\right| < \epsilon$,极限确实是 0。$\square$
Remark. 这东西很类似于某种 $\infty / \infty$ 的洛必达,但是不完全一样,所以其证明可能会给你一些启发。
解析几何
基本上都是送分。只有少量要点。
二次曲面的形状判定
下面的讨论规定标准型二次曲面如何产生。
对于二次项,可以通过合同变换,化成规范型。
剩下的一次项,若和二次项同时出现,那么可以平移吃掉一次项。
如果出现两个没有二次项的一次项,通过合同变换,可以变为一个一次项。
一次项和常数项同时出现,则可以平移吃掉常数项。
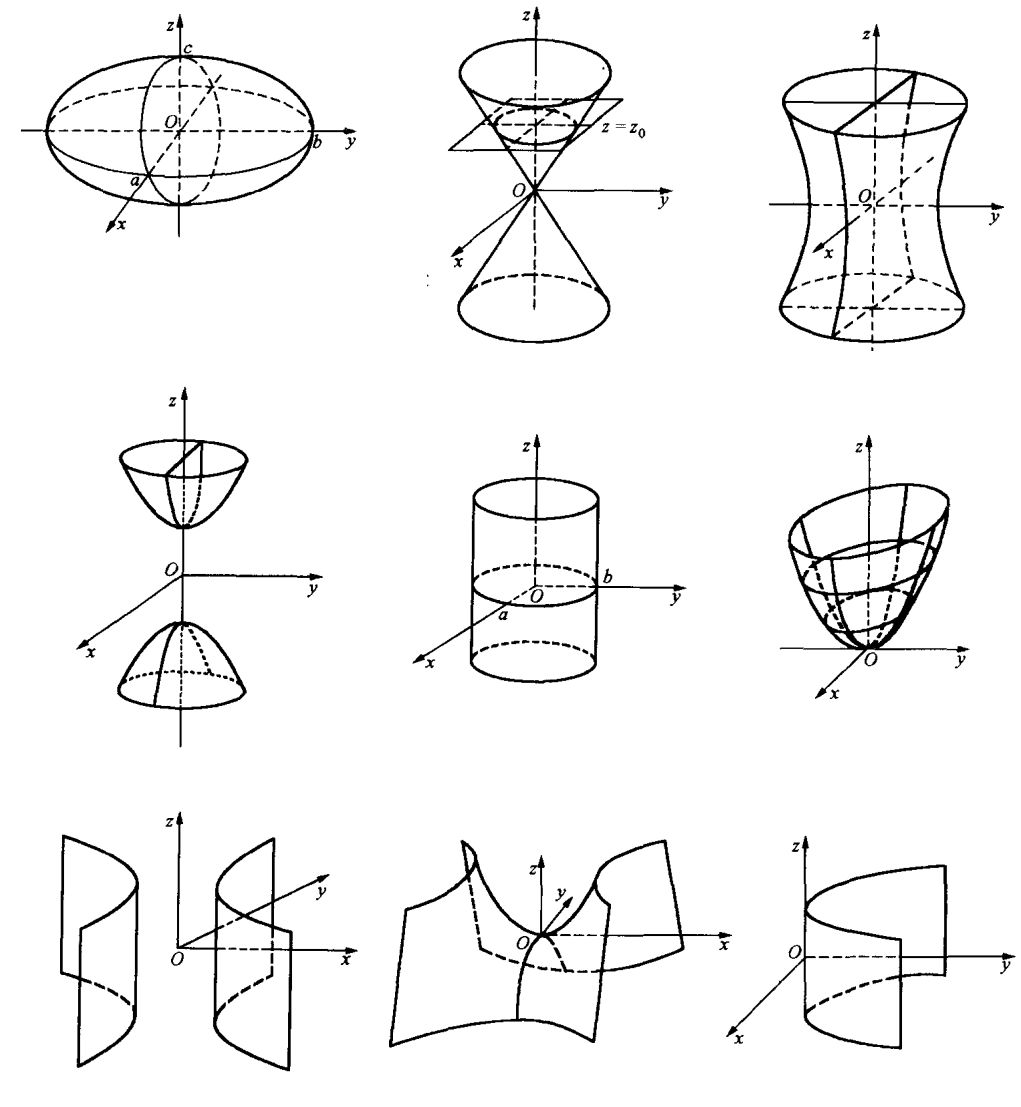
综合下来,按照秩,正惯性指数,是否有额外的一次项,常数项符号分类讨论,得到如下几种标准型及其形状:
| 编号 | 标准型 | 形状 | 简要解释 |
|---|---|---|---|
| 1 | $x^2 + y^2 + z^2 = 1$ | 球面 | 欧几里得距离相同。 |
| 2 | $x^2 + y^2 - z^2 = 0$ | 圆锥面 | 水平截面圆半径等于纵截距的绝对值。 |
| 3 | $x^2 + y^2 - z^2 = 1$ | 单叶双曲面 | 换元(旋转体) $r^2 = x^2 + y^2$ 得双曲线。 |
| 4 | $x^2 + y^2 - z^2 = -1$ | 双叶双曲面 | 同理,但注意焦点在 $z$ 轴上。 |
| 5 | $x^2 + y^2 = 1$ | 圆柱 | 显然。 |
| 6 | $x^2 + y^2 - z = 0$ | 抛物面 | 换元(旋转体) $r^2 = x^2 + y^2$ 的抛物线。 |
| 7 | $x^2 - y^2 = 1$ | 双曲柱面 | 显然。 |
| 8 | $x^2 - y^2 - z = 0$ | 双曲抛物面(马鞍面) | 观察诸横截面。 |
| 9 | $x^2 - y = 0$ | 抛物柱面 | 显然。 |
九种二次曲面的图像如下
多元函数微分学
简单点集拓扑
在欧几里得空间 $\mathbb{R}^n$ 上定义如下概念:
定义 1.(距离) $d(P, Q) = ||\overrightarrow{PQ}||$
定义 2.(邻域) $U(P, r) = \{Q \in \mathbb{R}^n | d(P, Q) < r\}$,也称为开球。
给定集合 $E$,$\mathbb{R}^n$ 中的点可以分为三类:
- 内点 $\{P \in \mathbb{R}^n | \exists r. U(P, r) \subset E \}$。
- 外点 $\{P \in \mathbb{R}^n | \exists r. U(P, r) \cap E = \varnothing \}$。
- 边界 Otherwise。记为 $\partial E$。
$\partial E \subset E$ 称 $E$ 为闭集,$E$ 中只有内点称为开集。注意很多集合非开也非闭,$\varnothing$ 和 $\mathbb{R}^n$ 既是开集也是闭集。
$E$ 中任意两点可以被连续的曲线连接称为连通,连通开集称为区域。这一点不严谨,水平有限我们暂时也没办法补全。
命题 1. 开集的补是闭集。
Proof.
不难证明取补之后,内点和外点对换,边界保持。$\partial \mathbb{R}^n \setminus E = \partial E \in \mathbb{R}^n \setminus E$,因此是闭集。$\square$
命题 2. $U_i$ 为开集,则 $\bigcup\limits_{i=1}^{\infty} u_i$ 开。
Proof.
取 $P \in \bigcup\limits_{i=1}^{\infty} u_i$,因为 $U_i$ 均开,$P$ 为某个个集合 $U_j$ 的内点,因此存在 $\delta, U(P, \delta)\in U_j \subset \bigcup\limits_{i=1}^{\infty} u_i$,因此 $P$ 为并集的内点。符合开集的定义。$\square$
注意无穷多个开集交集不一定开。比如取两条不平行直线,其他 $U$ 均是包含交点的开集,最后交集为单点,是闭集。
命题 3. $\bar E = E \cup \partial E$,$\bar E$ 为闭集。
Proof.
由命题 3 只需要证明其其补为开集,也就是外点构成的集合为开集。若 $P$ 为外点,存在 $r$ 使得 $U(P, r) \cap E = \varnothing$。我们证明 $U(P, r)$ 中的点均为外点。
考虑 $Q\in U(P, r)$,令 $r’ = ||PQ||$,范数满足三角形不等式,因此 $U(Q, r-r’)\in U(P, r)$,可知 $U(Q, r-r’) \cap E = \varnothing$,$Q$ 为内点。$\square$
命题 4. $E\subset F$,$F$ 为闭集,则 $\bar E \subset F$。
这个命题的意义是闭包是包含一个集合的最小闭集。
Proof.
显然内点都必须属于 $F$,而若 $x\in \partial E$ 但 $x\notin F$,可知 $x\in \partial F$,这与 $F$ 闭矛盾。$\square$
命题 5. $\overline{A\cup B} = \bar A \cup \bar B$。
Proof.
$\supset$. $A\subset A\cup B \Rightarrow A \subset \overline{A\cup B}$,由命题 5 可知 $\bar A\subset \overline{A\cup B}$。同理 $\bar B \subset \overline{A\cup B}$。于是 $\overline{A\cup B} \supset \bar A \cup \bar B$。
$\subset$. $A\cup B \subset \bar A \cup \bar B$,由命题 5 可知 $\overline{A\cup B} \subset \bar A \cup \bar B$。
综上 $\overline{A\cup B} = \bar A \cup \bar B$。$\square$
有一个反直觉的反例:$A$ 连通 $\not\Rightarrow \bar A$ 连通。
反例.
$$
\left\{\left(x, \sin\left(\frac 1x\right)\right) \middle| x > 0 \right\}
$$
多元函数的极限与连续性
基本上是把单元函数中极限和连续的定义(用 $\epsilon-\delta$ 语言写,邻域换成上面的定义)直接照搬。诸四则运算法则
在证明极限的时候可能需要一些放缩(夹逼准则)。
Problem 1
$$
f(x, y) = \frac{x\sin y}{\sqrt{x^2 + y^2}}
$$
求 $\lim\limits_{(x, y)\rightarrow(0, 0)} f(x, y)$
Solution.
$$
\begin{aligned}
&\left|\frac{x\sin y}{\sqrt{x^2 + y^2}}\right|\\
\leq &\left|\frac{xy}{\sqrt{x^2 + y^2}}\right| \\
\leq &\left|\frac{x^2 + y^2}{2\sqrt{x^2 + y^2}}\right| \qquad (\text{GM-SM Inequality}) \\
= &\left|\frac 12\sqrt{x^2 + y^2}\right| \\
\rightarrow 0 ((x, y) \rightarrow (0, 0))
\end{aligned}
$$
此外还有一个常见的处理方法是极坐标换元。
求
$$
L=\lim_{(x, y)\rightarrow (0, 0)} (x^2 + y^2)\mathrm{e}^{-|x|-|y|}
$$
Solution.
极坐标换元得
$$
\begin{aligned}
L &= \lim_{r\rightarrow 0^{+}} r^2\mathrm{e}^{-r(|\sin x| + |\cos x|)} \\
&\leq \lim_{r\rightarrow 0^{+}} r^2\mathrm{e}^{-r} \\
&= 0
\end{aligned}
根据夹逼准则,$L = 0$。
$$
证明极限不存在仍然采用多路趋近的方法,需要注意累次极限的存在性和极限的存在性无关。
求证下列极限不存在
$$
\lim_{(x, y)\rightarrow (0, 0)} \frac{x^2y}{x^4 + y^2}
$$
Solution.
从 $y=kx$ 和 $y = x^2$ 趋近,发现极限不同。$\square$
性质.(有界闭区域上连续函数的性质) 有界性、最值性、介值性。
偏导数 全微分
注意求一个复杂函数在给定点处的偏导数时可以先代入数字。
$$
z = \arctan\frac{(x-2)y+y^2}{xy+(x-2)^2y^3}
$$
求 $\frac{\partial z}{\partial y}(2, 0)$
Hint.
你肯定不会想要先求偏导然后代入数字。
定理.* 两个二阶混合偏导数若连续,则相等。
证略。
$$
\Delta z = A\Delta x + B\Delta y + o(\rho)
$$
记为
$$
\mathrm{d}z = A\mathrm{d}x + B\mathrm{d}y
$$
定理 1. 可微 $\Rightarrow$ 连续。
Proof.
$\rho\rightarrow 0$ 时 $\Delta x, \Delta y \rightarrow 0$,因此
$$
\Delta z = A\Delta x + B\Delta y + o(\rho) \rightarrow 0
$$
$\square$
定理 2. 函数可微 $\Rightarrow$ 偏导存在。
Proof.
$$
\frac{\partial z}{\partial x} = \lim_{\Delta x\rightarrow 0}\frac{\Delta z}{\Delta x} = \lim_{\Delta x\rightarrow 0}\frac{A\Delta x + o(\rho)}{\Delta x} = A
$$
其他变元同理。$\square$
定理 3. 偏导存在且连续 $\Rightarrow$ 可微。
Proof.
$$
\begin{aligned}
\Delta z &= f(x_0 + \Delta x, y_0 + \Delta y) - f(x_0, y_0) \\
&= f(x_0 + \Delta x, y_0 + \Delta y) - f(x_0, y_0 + Delta y) + f(x_0, y_0 + Delta y) - f(x_0, y_0) \\
&= \frac{\partial f}{\partial x}(x_0 + \theta_0\Delta x, y_0 + \Delta y)\Delta x + \frac{\partial f}{\partial y}(x_0, y_0 + \theta_2\Delta y)\Delta y\\
=& \frac{\partial f}{\partial x}(x_0, y_0)\Delta x + \frac{\partial f}{\partial y}(x_0, y_0)\Delta y + {\color{blue} \alpha_1\Delta x + \alpha_2\Delta y}
\end{aligned}
$$
其中
$$
\begin{aligned}
\alpha_1 &= \frac{\partial f}{\partial x}(x_0 + \theta_0\Delta x, y_0 + \Delta y) - \frac{\partial f}{\partial x}(x_0, y_0)\Delta x \\
\alpha_2 &= \frac{\partial f}{\partial y}(x_0, y_0 + \theta_2\Delta y)\Delta y - \frac{\partial f}{\partial y}(x_0, y_0)\Delta y
\end{aligned}
$$
通过连续性可以证明蓝色部分为 $o(\rho)$。$\square$
链式法则仍然成立。
高阶全微分可以简单地写作如下形式:
$$
\mathrm{d}^n = (\frac{\partial}{\partial x}\mathrm{d}x + \frac{\partial}{\partial y}\mathrm{d}y)^n
$$
证明不可微可以分为下面两类:
- 偏导不存在,必然不可微。
- 不连续,必然不可微。
- 偏导存在,则证明
$$
0\ne \lim_{\rho\rightarrow 0} \frac{f(x, y) - \partial_x f\Delta x - \partial_y f \Delta y}{\rho}
$$
方向导数 梯度
梯度定义为
$$
\nabla f = \left(\frac{\partial}{\partial x}, \frac{\partial}{\partial y}\right)
$$
沿 $\vec l$ 的方向导数定义为($\vec l$ 的方向余弦为 $(\cos \alpha, \cos\beta)$)
$$
\frac{\partial f}{\partial \vec l}=\lim_{t\rightarrow 0}\frac{f(x + t\cos\alpha, y + t\cos\beta) - f(x, y)}{t}
$$
在可微的条件下,很显然(用微分估计一下立即得到)
$$
\frac{\partial f}{\partial \vec l} = (\cos \alpha, \cos\beta) \cdot \nabla f
$$
中值定理 泰勒公式
在上一节建立的方向导数和偏导数的关系之下,我们发现这两个东西就是在多元函数定义域上拉出一条线,然后变成单元的中值定理和泰勒公式。
泰勒公式的唯一性仍然成立,故导出了如下的计算技巧:对于对于乘积式,先计算因子的展开式,然后乘起来。
有一个重要的应用如下。
命题. 函数 $f(u, v)$ 满足 $\partial_u \equiv 0$,那么存在 $F(v)$ 使得 $f(u, v) \equiv F(v)$。
Proof Sketch.
拉格朗日中值定理。
可以推出两条三角换元性质:
info.
$x\partial_x f(x, y) + y\partial_y f(x, y) = 0\Rightarrow f(r\cos\theta, r\sin\theta) = F(\theta)$
info.
$x\partial_x f(x, y) - y\partial_y f(x, y) = 0\Rightarrow f(r\cos\theta, r\sin\theta) = F(r)$
隐函数存在定理 逆映射存在定理
不想记忆任何结论,完全模拟一元微积分学中隐函数求导、反函数求导的操作,利用一阶微分形式不变性解方程。
极值
讨论一下如何记忆极值的充分条件。首先我们将 $f(x + \Delta x, y + \Delta y) - f(x, y)$ 展开到二阶小量,带拉格朗日余项,发现它是
$$
\begin{aligned}
&\partial_{xx}(x + \theta\Delta x, y + \theta\Delta y)\Delta x^2 \\
+&2\partial_{xy}(x + \theta\Delta x, y + \theta\Delta y)\Delta x\Delta y \\
+&\partial_{yx}(x + \theta\Delta x, y + \theta\Delta y)\Delta y^2 \\
\end{aligned}
$$
我们令
$$
\begin{aligned}
A = \partial_{xx}(x, y) \\
B = \partial_{xy}(x, y) \\
C = \partial_{yy}(x, y)
\end{aligned}
$$
根据偏导连续性,一个小邻域内的正负性可以用 $A, B, C$ 模拟。那么上面的式子是一个关于 $x, y$ 的二次型,它的矩阵表示为(这个矩阵称为 Hessian,可以拓展到多维)
$$
\begin{pmatrix}
A & B \\
B & C
\end{pmatrix}
$$
极大值即要求这个矩阵负定,极小值要求这个矩阵正定。根据线性代数知识,我们需要讨论顺序主子式的正负性。
- 若 $AC - B^2 > 0$
- 若 $A > 0$,正定,得到极小值。
- 若 $A < 0$,负定,得到极大值。
- 若 $AC - B^2 < 0$
- 矩阵一定不定,得到鞍点。
- 若 $AC - B^2 = 0$,需要看更高阶小量,暂时无法判断。