Tensor Analysis (1) Vectors and Tensors

Posted on Edited on In , ,

Abstract. 参考资料是 James G Simmonds 的 A Brief on Tensor Analysis。

本章是向量代数和张量代数基础。

如非特殊说明下面的讨论均在三维欧几里得空间 $E_3$ 中进行。

Directed Line Segments

即有向线段，或称为 arrow。从 $A$ 指向 $B$ 的 arrow 记作 $\overline{AB}$。$A$ 称为此 arrow 的 tail，$B$ 称为 head。

称两个 arrow 等价，当其可以在平移变换下重合。vector 是 arrow 在此等价关系下的商集。

向量 $\mathbf{v}$ 的长度记为 $|\mathbf{v}|$。对于一个非零向量 $\mathbf{v}$，称如下的式子为 $\mathbf{v}$ 的方向

$$
\overline{\mathbf{v}} = \frac{\mathbf{v}}{|\mathbf{v}|}
$$

零向量没有方向。

可以在 $E_3$ 选择任意的原点 $O$，称 $\overline{OP}$ 对应的向量 $\mathbf{x}$ 为 $P$ 的坐标，此时 $P$ 点简记为 $P(\mathbf{x})$。

Addition, Multiplication by Scalar

加法和数乘，和常见的定义一致，这里不多讲。

Things That Vectors May Represent

物理中存在习见的可以用向量表示的量（位移，力，刚体定轴转动等）。但是在表示时需要注意如下几点：

  1. 单位不同的对象分属不同的向量空间。否则我们将可以把一个力和位移相加，这很明显是不对的。
  2. 向量的加法不一定能够反应该对象的叠加。比如说刚体绕定点的转动。

Cartesian Coordinates

书中的坐标是用到坐标平面的距离定义的，即 $P(x, y, z)$，则 $|x|$ 是 $P$ 到 $yz-$面的距离，符号由其所在的方向决定（这里定义了坐标平面的正反面，无非是一些比较琐碎的东西）。

采用如下记号记录一个向量的坐标 $\mathbf{v}\sim (v_x, v_y, v_z)$。

此时在坐标表示下加法，数乘，长度都可以方便地表示。

The Dot Product

$$
\mathbf{u}\cdot \mathbf{v} = |\mathbf{u}||\mathbf{v}|\cos\theta
$$

事实上点乘的分配性并不显然，我们先绕过正交分解推导点乘的坐标表示。

用勾股定理证明余弦定理，得到

$$
\mathbf{u}\cdot \mathbf{v} = \frac 12(|\mathbf{u}|^2 + |\mathbf{v}|^2 - |\mathbf{u} - \mathbf{v}|^2)
$$

将所有模长用坐标展开（基于勾股定理，不需要结合性）得到

$$
\mathbf{u}\cdot \mathbf{v} = u_xv_x + u_yv_y + u_zv_z
$$

基于此结论可以导出点乘的分配律

$$
\mathbf{u}\cdot (\mathbf{v} + \mathbf{w}) = \mathbf{u}\cdot \mathbf{v} + \mathbf{u}\cdot \mathbf{w}
$$

The Cross Product

向量叉乘用来表示两个作为邻边的平行四边形的有向面积（Right oriented area of a parallelogram），即

$$
|\mathbf{u}\times \mathbf{v}| = |\mathbf{u}||\mathbf{v}|\sin \theta
$$

其方向由右手定则确定，垂直于 $\mathbf{u}, \mathbf{v}$ 所在的平面。

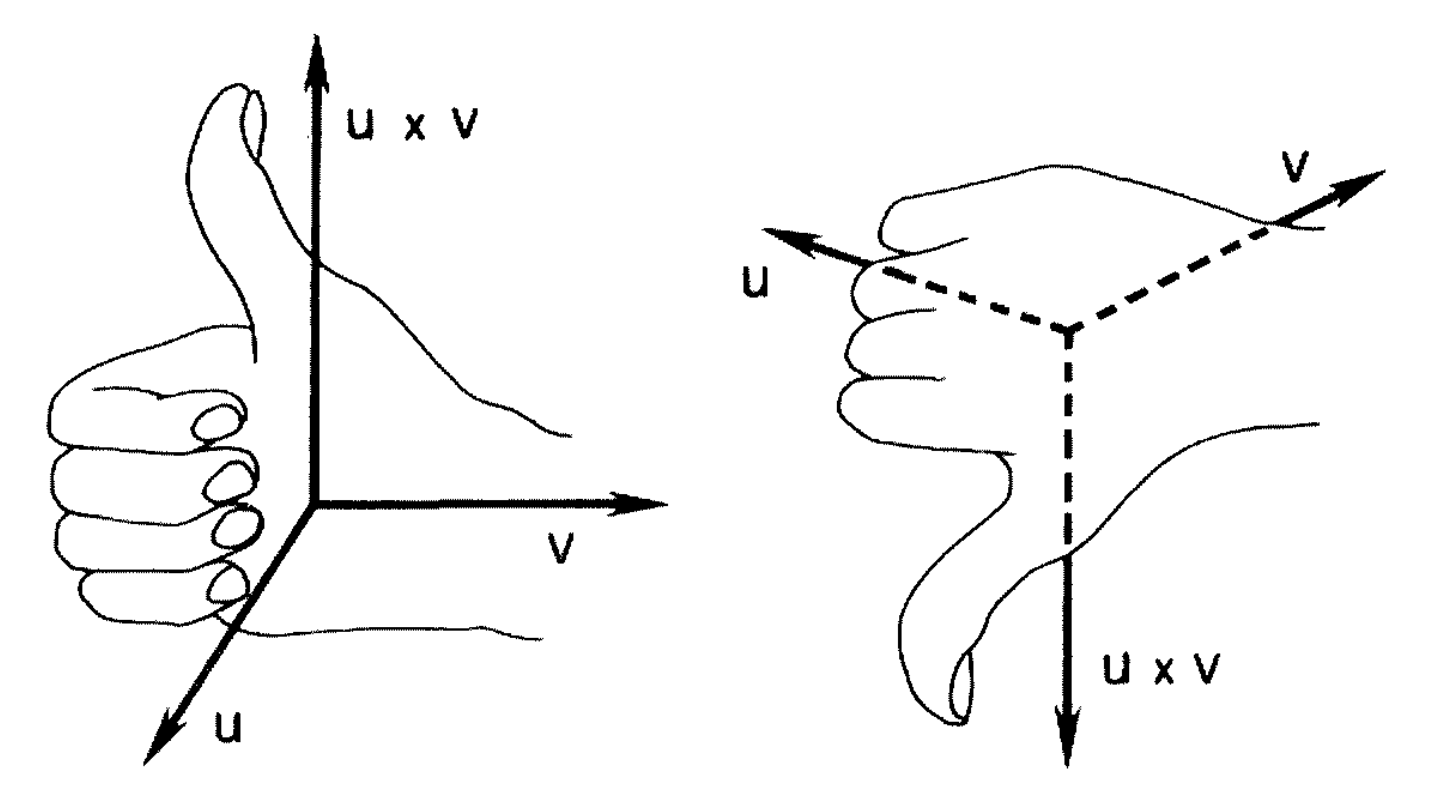
根据定义可以知道

$$
\mathbf{u}\times \mathbf{v} = -\mathbf{v}\times \mathbf{v}
$$

更近一步地，我们考虑 $\mathbf{u}, \mathbf{v}, \mathbf{w}$ 作为三条相邻棱的平行六面体体积，用一个重要的向量混合积（三重标量积，scalar triple product） $\mathrm{vol}(\mathbf{u}, \mathbf{v}, \mathbf{w}) = (\mathbf{u}\times \mathbf{v})\cdot\mathbf{w}$。这也是一种有向体积。

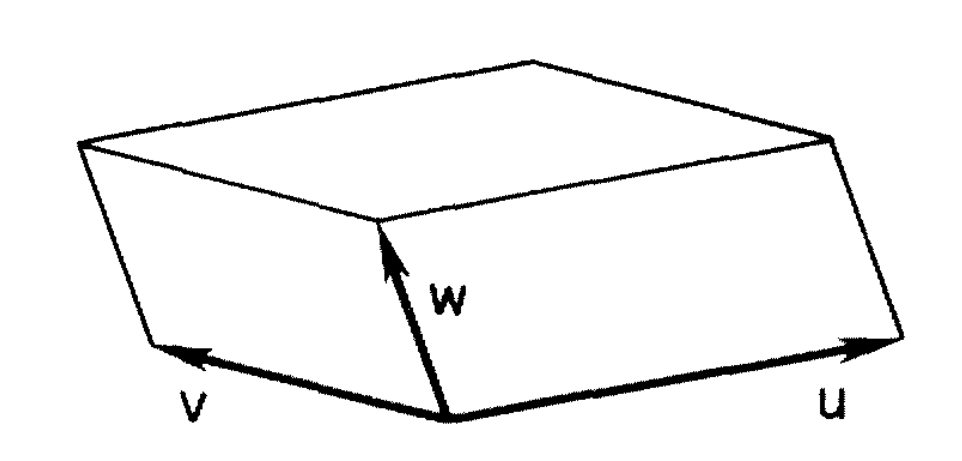
如果 $\mathbf{u}, \mathbf{v}, \mathbf{w}$ 按顺序构成了一个右手系，依定义那么下面的式子显然成立。

$$
(\mathbf{u}\times \mathbf{v})\cdot\mathbf{w} = (\mathbf{v}\times \mathbf{w})\cdot\mathbf{u} = (\mathbf{w}\times \mathbf{u})\cdot\mathbf{v} \geq 0
$$

当不构成右手系时不等号左边的等式还是成立的，不等号会变号（由对称性简单的导出）。换言之 $\mathrm{vol}(\mathbf{u}, \mathbf{v}, \mathbf{w})$ 是一个循环不变量。

接下来我们验证叉乘有分配律。

Lemma 1.

$$
\mathbf{a} = \mathbf{b} \Leftrightarrow \mathbf{a}\cdot \mathbf{b} \equiv \mathbf{b}\cdot \mathbf{c} (\forall \mathbf{c})
$$

Proof.

$$
\mathbf{a}\sim (\mathbf{a}\cdot\mathbf{e}_x,\mathbf{a}\cdot\mathbf{e}_y,\mathbf{a}\cdot\mathbf{e}_z)
$$

因此：

  • $\Rightarrow$. $\mathbf{a}\cdot\mathbf{e}_i = \mathbf{b}\cdot\mathbf{e}_i$，将 $\mathbf{c}$ 正交分解，根据 dot product 的分配律可以得到结论。
  • $\Leftarrow$. $\forall \mathbf{c}, \mathbf{a}\cdot \mathbf{c} = \mathbf{b}\cdot\mathbf{c}$ 隐含 $\mathbf{c} = \mathbf{e}_i$ 的情况。根据开头给出的式子有 $\mathbf{a} = \mathbf{b}$。

$\square$

Theorem 1 (叉乘的分配律).

只需验证一边分配律。根据引理只需要证明 $\forall \mathbf{c}$

$$
(\mathbf{u}\times(\mathbf{v} + \mathbf{w}))\cdot\mathbf{c} = (\mathbf{u}\times\mathbf{v} + \mathbf{u}\times\mathbf{w})\cdot\mathbf{c}
$$

利用循环不变性对左边进行化简。

$$
\begin{aligned}
(\mathbf{u}\times(\mathbf{v} + \mathbf{w}))\cdot\mathbf{c} =& (\mathbf{c}\times\mathbf{u})\cdot(\mathbf{v} + \mathbf{w}) \\
=& (\mathbf{c}\times\mathbf{u})\cdot\mathbf{v} + (\mathbf{c}\times\mathbf{u})\cdot\mathbf{w}\\
=&\mathrm{RHS}
\end{aligned}
$$

因此分配律成立。$\square$

书上有一个例题比较有意思。

Problem 1. 不使用正交分解的做法，证明如下恒等式：

$$
(\mathbf{u}\times\mathbf{v})\times\mathbf{w} = (\mathbf{u}\cdot\mathbf{w})\mathbf{v} - (\mathbf{v}\cdot\mathbf{w})\mathbf{u}
$$

Proof

如果 $\mathbf{u}, \mathbf{v}$ 共线那么显然成立，方便起见我们只考虑不共线的情况。

$(\mathbf{u}\times\mathbf{v})\times\mathbf{w}\perp(\mathbf{u}\times\mathbf{v})$，因此在 $\mathbf{u}, \mathbf{v}$ 张成的平面内[1]，即 $\mathrm{LHS} = A\mathbf{u} + B\mathbf{v}$。

类似于 Lemma 1 我们可以证明下面的引理（感性理解起来非常容易，证明可以验证一个线性方程组解的唯一性）：

Lemma. 若 $\mathbf{w}_1, \mathbf{w}_2 \in \langle \mathbf{a}, \mathbf{b} \rangle$，那么

$$
\mathbf{w}_1 = \mathbf{w}_2 \Leftrightarrow \mathbf{w}_1\cdot\mathbf{a} = \mathbf{w}_2\cdot\mathbf{a} \land \mathbf{w}_1\cdot\mathbf{b} = \mathbf{w}_2\cdot\mathbf{b}
$$

接下来我们直接验证等式。给两边左乘 $u$，然后轮换得到

$$
(\mathbf{u}\times(\mathbf{u}\times\mathbf{v})\cdot\mathbf{w}) = (\mathbf{u}\cdot\mathbf{v})(\mathbf{u}\cdot\mathbf{w}) - \mathbf{u}^2(\mathbf{v}\cdot\mathbf{w})
$$

数乘可以放进点乘里面，点乘对加法可分配，于是后面的项里面可以直接提出来一个 $\cdot\mathbf{w}$，于是我们只需要验证

$$
\mathbf{u}\times(\mathbf{u}\times\mathbf{v}) = (\mathbf{u}\cdot\mathbf{v})\mathbf{u} - \mathbf{u}^2\mathbf{v}
$$

根据 Lemma 1 我们还是只需要两边 $\cdot\mathbf{u}, \cdot\mathbf{v}$ 验证。$\cdot\mathbf{u}$ 之后两边都是 $0$。而 $\cdot\mathbf{v}$ 之后轮换，即验证

$$
-(\mathbf{u}\times\mathbf{v})^2 = (\mathbf{u}\cdot\mathbf{v})^2 - \mathbf{u}^2\mathbf{v}^2
$$

所有乘法按定义拆开即可证明相等。

而给原式两边点乘 $\mathbf{v}$ 的验证思路也是一样的。

感觉这个证明比较强行，但是比较智慧。书上的证明更厉害一点，他甚至不是验证，而是直接从左边推到了右边。

另外不难验证 $\mathbb{R}^3$ 当中向量叉积和上面的重要混合积可以用行列式的形式写出。

$$
\mathbf{u}\times\mathbf{v} = \left|\begin{matrix}
\mathbf{e}_x & \mathbf{e}_y & \mathbf{e}_z \\
u_x & u_y & u_z \\
v_x & v_y & v_z
\end{matrix}\right|, (\mathbf{u}\times\mathbf{v})\cdot\mathbf{w} = \left|\begin{matrix}
w_x & w_y & w_z \\
u_x & u_y & u_z \\
v_x & v_y & v_z
\end{matrix}\right|
$$

同时可以通过行列式的性质导出上面的轮换不变性。

Aternative Interpretation of the Dot and Cross Product. Tensors

接下来我们从向量过渡到张量。

考虑点乘的另一种解释。类似于 FP 中 Curry 化的思想，我们可以将 $\mathbf{F}\cdot$ 看成一个从向量到实数的映射。事实上我们可以验证这个映射是一个线性映射。

同理，在 $\mathbf{u}\times\mathbf{v}$ 中，我们将 $\mathbf{u}\times$ 看成一个从向量到向量的映射，我们也可以验证这个是线性映射。这种从向量到向量的线性映射称为二阶张量（2nd order tensors）。

最简单的二阶张量之一是投影

$$
\mathrm{Proj}_u(\mathbf{v}) = (\mathbf{v}\cdot\overline{\mathbf{u}})\overline{\mathbf{u}}
$$

不难验证 $\mathrm{Proj}_u$ 是一个线性映射，所以它是一个张量。

上面的定义式启发我们进行如下拓展。

Definition. 定义 $\mathbf{u}, \mathbf{v}$ 的直积 $\mathbf{uv}$ 为如下满足如下映射规则的张量：

$$
\mathbf{uv}(w) = \mathbf{u}(\mathbf{v}\cdot\mathbf{w})
$$

那么

$$
\mathrm{Proj}_u = \overline{\mathbf{u}}\overline{\mathbf{u}}
$$

Definitions

之前我们定义了二阶张量是 $\mathbb{R}^3\rightarrow\mathbb{R}^3$ 的线性映射[2]，接下来我们从更加抽象的高度来看待这件事情。

采用如下记号来表示张量 $\mathbf{T}$ 作用在一个向量 $\mathbf{v}$ 上 $\mathbf{Tv}$。

Definition 1 (张量的相等关系)

$$
\mathbf{S} = \mathbf{T} \Leftrightarrow \mathbf{Sv} = \mathbf{Tv}, \forall \mathbf{v}
$$

或者根据 Lemma 1，写成如下的等价形式

$$
\mathbf{S} = \mathbf{T} \Leftrightarrow \mathbf{u}\cdot\mathbf{Sv} = \mathbf{u}\cdot\mathbf{Tv}, \forall \mathbf{u}, \mathbf{v}
$$

Definition 2 (张量的转置) 存在唯一的二阶张量 $\mathbf{T}^T$ 使得

$$
\mathbf{u}\cdot\mathbf{Tv} = \mathbf{v}\cdot\mathbf{T}^T\mathbf{u}, \forall \mathbf{u}, \mathbf{v}
$$

张量可以具有下述性质：

  1. Symmetric. （对称性）若 $\mathbf{T} = \mathbf{T}^T$。
  2. Antisymmetric （反对称性）若 $\mathbf{T} = -\mathbf{T}^T$。
  3. Singular （奇异性）若 $\exists \mathbf{v}\ne 0, \mathbf{Tv} = 0$。

其实你发现这个性质和矩阵的相应性质之间存在同构关系。类似地我们可以证明如下命题：

Proposition 1 任意的二阶张量可以被（唯一）拆成一个对称张量和一个反对称张量的和。拆分方法如下：

$$
\mathbf{T} = \frac 12(\mathbf{T} + \mathbf{T}^T) + \frac 12(\mathbf{T} - \mathbf{T}^T)
$$

The Cartesian Components of a 2nd Order Tensor

考虑计算 $\mathbf{Tv}$，先对 $\mathbf{v}$ 正交分解

$$
\begin{aligned}
\mathbf{Tv} =& \mathbf{T}(v_x\mathbf{e}_x + v_y\mathbf{e}_y + v_z\mathbf{e}_z) \\
=&v_x\mathbf{Te}_x + v_z\mathbf{Te}_z + v_z\mathbf{Te}_z
\end{aligned}
$$

接下来对 $\mathbf{Te}_i$ 都进行正交分解。

$$
\begin{aligned}
\mathbf{Tv} =& v_x(T_{xx}\mathbf{e}_x + T_{xy}\mathbf{e}_y + T_{xz}\mathbf{e}_z) \\
+& v_y(T_{yx}\mathbf{e}_x + T_{yy}\mathbf{e}_y + T_{yz}\mathbf{e}_z) \\
+& v_z(T_{zx}\mathbf{e}_x + T_{zy}\mathbf{e}_y + T_{zz}\mathbf{e}_z)
\end{aligned}\tag{*}
$$

可以发现张量都能写成这种矩阵的形式，记为 $\mathbf{T}\sin T$，于是 $\mathbf{T}^T\sim T^T$，也是唯一的。

此外根据上面的式子我们可以知道

$$
T_{ij} = \mathbf{e}_i\mathbf{T}\mathbf{e}_j (i, j \leftarrow x, y, z)
$$

The Cartesian Basis for 2nd Order Tensors

我们知道三位欧几里得空间中有标准正交基 $\mathbf{e}_x, \mathbf{e}_y, \mathbf{e}_z$，我们考虑在二阶张量中也找到类似的基。

考察 $(*)$ 式，基于以下事实：

$$
v_x = \mathbf{v}\cdot\mathbf{e}_x, v_y = \mathbf{v}\cdot\mathbf{e}_y, v_z = \mathbf{v}\cdot\mathbf{e}_z
$$

以及我们在第 7 节中定义的通过直积构造的张量

$$
\mathbf{uv}(w) = \mathbf{u}(\mathbf{v}\cdot\mathbf{w})
$$

那么 $v_xT_{xx}\mathbf{e}_x = T_{xx}(\mathbf{e}_x\cdot\mathbf{v})\mathbf{e}_x = T_{xx}\mathbf{e}_x\mathbf{e_x}(\mathbf{v})$，其他分量同理

于是我们得到了

$$
\mathbf{T} = T_{xx}\mathbf{e}_x\mathbf{e}_x + T_{xy}\mathbf{e}_x\mathbf{e}_y + \cdots
$$

下面我们证明这个表示唯一。假设存在 $\mathbf{T} = T’_{xx}\mathbf{e}_x\mathbf{e}_x + T’_{xy}\mathbf{e}_x\mathbf{e}_y + \cdots$，做差后应有

$$
[(T_{xx} - T’_{xx})\mathbf{e}_x\mathbf{e}_x + (T_{xy} - T’_{xy})\mathbf{e}_x\mathbf{e}_y + \cdots]\mathbf{v} = 0
$$

两边点乘根据 Lemma 1 其等价于

$$
\mathbf{u}\cdot[(T_{xx} - T’_{xx})\mathbf{e}_x\mathbf{e}_x + (T_{xy} - T’_{xy})\mathbf{e}_x\mathbf{e}_y + \cdots]\mathbf{v} = 0
$$

取 $\mathbf{u} = \mathbf{e}_i, \mathbf{v} = \mathbf{e}_j$ 可以得到 $T_{ij} - T’_{ij} = 0$。因此表示方法唯一。

  1. 1.证明可以考虑取 $\mathbf{u}, \mathbf{v}, \mathbf{u}\times \mathbf{v}$，可以证明这是 $\mathbb{R}^3$ 的一组基。然后不难证明目标向量没有 $\mathbf{u}\times \mathbf{v}$ 方向的分量。 ↩
  2. 2.这个 $\mathbb{R}$ 在更广义的理论中可以换成别的数域，物理中经常是 $\mathbb{C}$。 ↩