Infomation and Entropy (1) Bits

Posted on Edited on In , ,

参考资料：Information and Entropy by Prof. Paul Penfield

Abstract. 讲了各种 bit。科普性质比较大，里面除了量子比特之外涉及的知识都是常识的真子集。

度量信息的基本单位是 bits。

通过考虑下列情景来体会信息的度量：

  • 一个人抛硬币（两种结果），告知另一个人结果。
  • 一个人从一副牌里面抽一张（$13\times 4$ 种结果），告知另一人结果。

对于第一个例子，我们将正反面映射到 $0, 1$。那么结果或者是 $0$，或者是 $1$。此时我们称传递这个信息需要 $1$ bit。类似地，如果平行重复实验 $n$ 次，将每次的结果排列起来，我们就可以将共 $2^n$ 种结果用 $n$ 个比特传递。可见信息的量是 $\log_2(N)$，其中 $N$ 指可能的结果数量。

注意传递信息需要两个步骤：

  1. Setup. 两人约定一个从结果到 $01$ 串的一一对应，称为编码。
  2. Outcome. 发送者将信息以此一一对应编码后，发送给接收者。

动态地考虑这个过程，接收者在知晓一个结果产生之后，他对此结果有一个 uncertainty，这个 uncertainty 也可以用 bits 来表达。在接受到发送者发送的编码之后，他的 uncertainty 因为接收到信息而缩小。因此接收者的 uncertainty 在 setup 阶段上升，在 outcome 阶段下降。

上述的例子表面。信息有下述的性质：

  • 信息可以通过观察、实验、测量获得。
  • 信息是主观的，取决于观测者。（发送方和接收方知道的信息是不一样的，否则将不存在交流的必要）
  • uncertainty 因接收到“存在一个 observation 使得某个信息可以获得”而增加，因接收到该信息而降低。
  • 信息有损失，或者因为数据自身而损失，或者在编码过程中损失。
  • 信息存在的物理形式局限于时间和空间，因而可以可以被发送、存储和提取。

The Boolean Bit

上述过程中用到的 $01$ 序列种的每一位称为 Boolean Bit。

为了进行进一步的讨论，我们需要一些布尔代数。

考虑 $S = {0, 1}$，此时 $S\mapsto S$ 的一元函数有且仅有以下四种：IDENTITY，NOT，ZERO，ONE（名字直接的解释了作用）。

接下来考虑考虑二元函数。很明显一共有 $16$ 种，其中常用的有 AND，OR，XOR，NAND（not and），NOR（not or）这些函数实际上我们都很熟悉，因此这里不再列真值表。

可以发现 AND 的效果类似于数域中的乘法，OR 类似于加法（实际上 XOR 更类似于加法），我们接受如下通用的记号：

$$
\begin{matrix}
NOT & \overline A \\
AND & A\cdot B \\
NAND & \overline{A\cdot B} \\
OR & A + B \\
NOR & \overline{A+B} \\
XOR & A \oplus B
\end{matrix}
$$

有一些实用的布尔函数的性质，比如：

  • Reversible. 根据结果可以推断出输入。比如说 $4$ 个单边缘函数种 IDENTITY 和 NOT 都是 Reversible 的。显而易见任何一个二元函数（只有一个输出）都不能是 Reversible 的。但是如果 $A\oplus B$ 同时返回结果和 $A$，那么它就是 Reversible 的。
  • Commutative. 即交换性。不多赘述。

另外布尔代数中还有下面的运算律：

注意 Boolean Bit 具有可复制性、可丢弃性（can be copied or discarded）。然而这个性质在量子的系统中不好，所以下面 $(1.3)$ 节中描述了量子比特的模型。

The Circuit Bit

一个将布尔表达式实体化的方式是组合逻辑电路。每一个布尔函数都可以对应一种门电路，如下表所示：

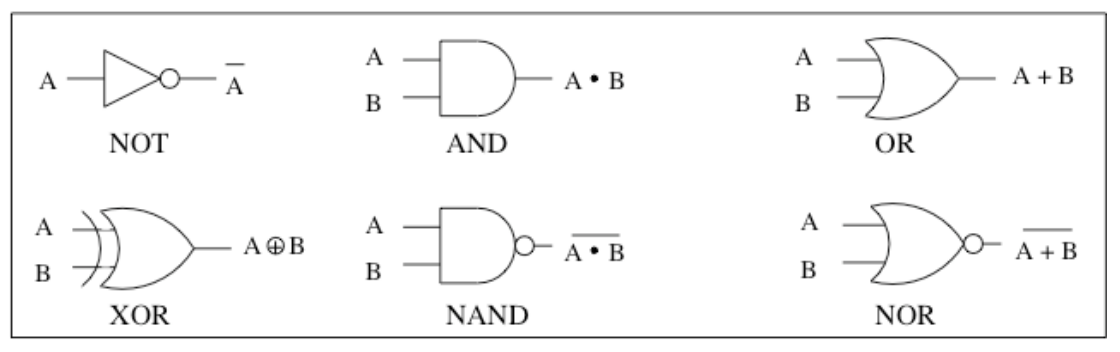
将门电路组合起来可以得到一些布尔表达式对应的电路。

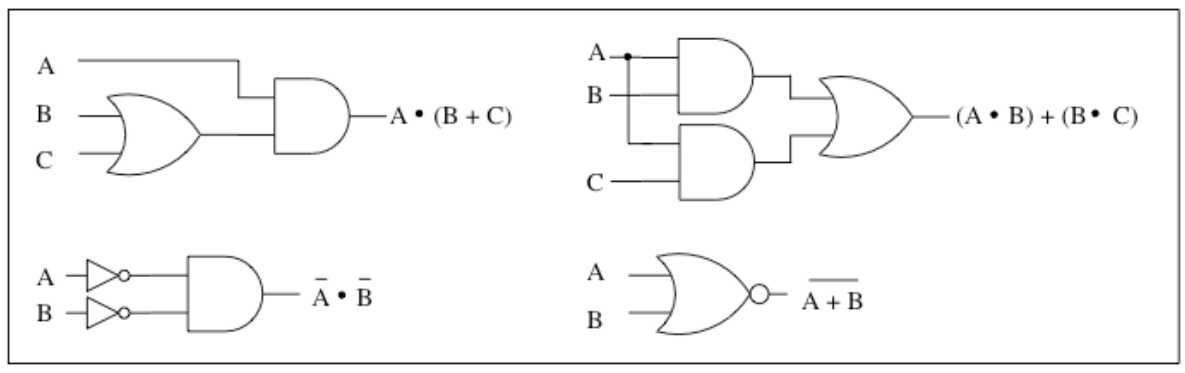
注意电路当中不应当有环，有环的逻辑电路称为时序逻辑电路，而布尔代数不适用于此类电路。

Circuit Bit 也具有上面的性质（复制就是重复电路，丢弃就是输出端什么都不接）。

The Control Bit

写在程序里面的控制流，形如 if P then A else B。

这东西的代数和 Boolean Bit 基本上是相同的，但是一个很有趣的差异是程序中存在短路运算，比如说一个 and 0 的参数的副作用会被废弃。

实际上我有点没搞懂这一节和信息有什么关系。

The Physical Bit

为了存储和传输信息，它必须要有一个物理的形式。

一个直观的想法是盒子里面放小球。但是为了工程上的需要我们希望盒子和小球尽量小。这个下界在量子力学中有所讨论，在这里我们的水平不足以涉及。

The Quantum Bit

量子力学告诉我们一个小物体可能有两种可以被测量出的状态，这个性质和 bit 非常相似，因此我们引入 qubit（量子比特）。qubit 的取值常被记作 $|0\rangle$ 和 $|1\rangle$ 而非 $0, 1$，在推广到多于 1 个量子比特的时候这个记号比较方便，而且它和实数 $0, 1$ 相区别。

量子力学中有三个特性，reversibility, superposition, entanglement，这使得 qubit 和传统的 bit 不同。

Reversibility. （可逆性）量子系统中的变换都是可逆的，因此 qubit 的代数中所有的函数都是 reversible 的，所以任何一个函数的输出都是不可丢弃（discard）的（不妨与 The Boolean Bit 一节中的性质对比）。但是在非封闭的量子系统中不可逆性会有两个来源：

  1. 该系统和一个无法观测的环境之间存在交互，导致系统中信息损失。
  2. 对系统状态的测量是不可逆的。

Superposition. （叠加性）在经典的情况下，每有一次测量我们就能确定这个 bit 的状态，而且我们可以重复测量多次。但是在量子系统中，我们还是只能问形如“测量对象是不是处于某态”的问题，然后得到一个确定的是/否的回答，且在此后的测量中我们将无法得到新的信息。我们也没法预知测量的结果，只能预知答案的概率分布。这个性质给单个 qubit 携带信息赋予了局限性和一些奇怪的机会。

考虑下面的例子。光的方向偏振可以用来存储 1 bit 的信息。现在 Alice 可以给 Bob 发送一个水平或垂直偏振的光量子，然后 Bob 测量它是否是垂直偏振的。如果答案是 Yes，那么 Bob 就可以推测这个 qubit 的状态是 $|1\rangle$。

那么我们思路打开，考虑除了水平垂直方向（称为 $\oplus$），再按其他方向，方便起见取 $\frac \pi 4, \frac {3\pi}{4}$ 方向发送光子（称为 $\otimes$）。此时如果选错了测量方向（下面称为偏振基），测量结果将是不确定的。具体地，测量结果将会以 $\cos^2 \theta$ 的概率出现 Yes，其中 $\theta$ 是选定的测量方向和实际偏振方向的夹角。而且在一次测量之后，该光子的偏振方向将会被“reset”至测量方向或者垂直于测量的方向。并且包括 Bob 在内的任何人都无法做到多次平行重复测量（包括直接多次测量和赋值光量子）

结合如下量子密钥分发的过程来理解上述“reset”的作用。

  1. Alice 随机密钥，对每一位随机偏振基 $\oplus, \otimes$，然后调制光子发送给 Bob。
  2. Bob 对于接收到的光子随机偏振基 $\oplus, \otimes$ 测量偏振方向，得到结果。
  3. 利用公开信道，Bob 将他选择的偏振基发送给 Alice，然后 Alice 返回选择正确的位置集合。可以知道这些正确的位置测量到的结果一定是正确的。
  4. Alice 和 Bob 在正确的位置的测量结果中选择一部分公开，如果不能对上说明有人窃听或者信息丢失，本次通讯作废。
  5. 如果没有人窃听，取没有公开的正确位置的测量结果作为密钥。

对于窃听者，他选择错误的偏振基的概率为 $\frac 12$，在此条件下得到错误结果的概率为 $\frac 12$，所以说对于一个公开的位，窃听者获得正确结果的概率是 $\frac 34$，假如说公开 $n$ 位，无法发现窃听者的概率只有 $1-\left(\frac 34\right)^n$，非常小。

Entanglement. （纠缠性）你可以通过某种方式产生两个或以上处于纠缠态的 qubit。这两个 qubit 可以被发送到不同的位置但是始终保持相同的方向，对一者的测量会影响到另一者。

需要注意的是量子系统也可以不表现出量子性，比如说独立产生 qubit 并且只用 $\oplus$ 调制，这样获得的 qubit 就和一般的 boolean bit 没有什么区别。

An Advantage of Qubits

似乎我们在 The Quantum Bit 一节中已经偷跑了书中这一节的内容，甚至更深入。

The Classical Bit

和 qubit 相对的，测量不会影响其状态的 bit 都叫做 qubit。

考虑到宏观物体也符合量子力学的定律，我们所谓的 classical bit 都是“近似的”完全不变的东西，随着集成电路的集成度越做越高，量子效应开始不可忽略。

疑似这个讲义写于 2015 年前。